Лекция
Привет, сегодня поговорим про отношение строгого порядка, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое отношение строгого порядка, отношение не строгого порядка , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Важный тип бинарных отношений - отношения порядка.
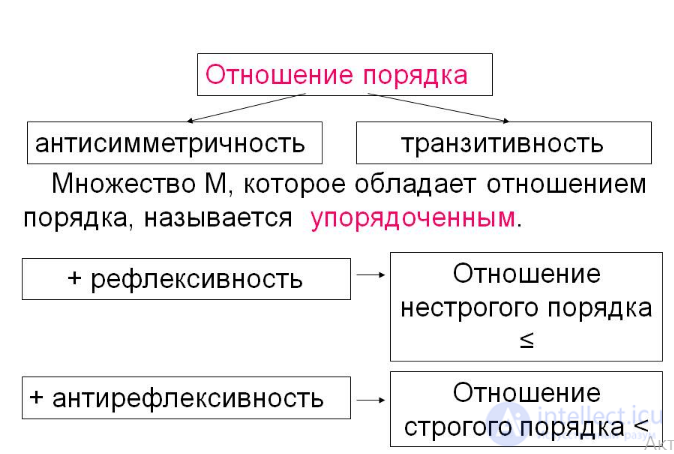
отношение строгого порядка - бинарное отношение, являющееся антирефлексивным, антисимметричным и транзитивным: обозначение - a{b (a предшествует b). Примерами могут служить отношения "больше", "меньше", "старше" и т.п. Для чисел обычное обозначение - знаки "<", ">".
Отношение нестрогого порядка - бинарное рефлексивное, антисимметричное и транзитивное отношение. Наряду с естественными примерами нестрогих неравенств для чисел примером может служить отношение между точками плоскости или пространства "находиться ближе к началу координат". Нестрогое неравенство для целых и действительных чисел можно также рассматривать как дизъюнкцию отношений равенства и строгого порядка.
Если в спортивном турнире не предусматривается дележа мест (т.е. каждый участник получает определенное, только ему присужденное место), то это пример строгого порядка; в противном случае - нестрогого.
Отношения порядка устанавливаются на множестве, когда для некоторых или всех пар его элементов определяется отношение предшествования a{b. Задание для множества некоторого отношения порядка называется его упорядочением, а само множество в результате этого становится упорядоченным. Отношения порядка могут вводиться разными способами. Для конечного множества любая перестановка его элементов задает некоторый строгий порядок. Бесконечное множество можно упорядочить бесконечным множеством способов. Представляют интерес только те упорядочения, которые имеют содержательный смысл.
Если для отношения порядка R на множестве М и некоторых различных элементов а,b 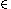 М выполняется хотя бы одно из отношений aRb или bRa , то элементы а и b называются сравнимыми; в противном случае - несравнимыми.
М выполняется хотя бы одно из отношений aRb или bRa , то элементы а и b называются сравнимыми; в противном случае - несравнимыми.
Если условие рефлексивности заменить на условие антирефлексивности:
,
то получим определение строгого, или антирефлексивного частичного порядка (обозначается обычно символом ).
Замечание. Об этом говорит сайт https://intellect.icu . Одновременная антирефлексивность и антисимметричность отношения влечет асимметричность, которое является более сильным условием, чем антисимметричность. Поэтому отношение является отношением строгого порядка тогда и только тогда, когда оно антирефлексивно и транзитивно.
В общем случае, если — транзитивное, антисимметричное отношение, то
— рефлексивный порядок
— строгий порядок.
Они обозначаются символом < и обладают свойствами:
Знаки и
изобретены Хэрриотом.
Отношение строгого порядка характерно для различного рода иерархий с подчинением одного объекта другому. Типичным примером отношений строгого порядка являются отношения «быть старше» и т. п., соответствующие математически строгому неравенству или строгому включению.
Если на множестве М задано отношение совершенно строгого порядка, то его элементы можно пронумеровать порядковыми числами 1, 2, ... , N, ..., т. е. каждому числу I можно поставить в соответствие некоторый элементХI Î М. Упорядоченное таким образом множество называется Последовательностью (конечной или бесконечной). Элемент ХI Î М называется Членом последовательности с индексом (номером) I. В этом случае соотношение ХI < ХJ будет выполняться только в том случае, если I < J. Если же порядок на множестве не является совершенным, т. е. множество частично строго упорядочено, то его элементы нельзя пронумеровать так, чтобы большим номерам соответствовали старшие элементы. Поэтому если элементы множества пронумерованы, то множество совершенно строго упорядочено. Нумерация элементов множества устанавливает совершенно строгий порядок на нем.
Надеюсь, эта статья про отношение строгого порядка, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое отношение строгого порядка, отношение не строгого порядка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про отношение строгого порядка
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.