Лекция
Привет, сегодня поговорим про матроид, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое матроид , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
матроид — классификация подмножеств некоторого множества, представляющая собой обобщение идеи независимости элементов, аналогично независимости элементов линейного пространства, на произвольное множество. Матроиды изучаются для анализа зависимости и независимости элементов множества, обладая широким применением в таких областях, как оптимизация, теория графов и комбинаторика.
Теория матроидов широко заимствует термины, используемые как в линейной алгебре , так и в теории графов , в основном потому, что это абстракция различных понятий, имеющих центральное значение в этих областях. Матроиды нашли применение в геометрии , топологии , комбинаторной оптимизации , теории сетей и теории кодирования
Матроид — пара 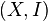 , где
, где 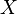 — конечное множество, называемое носителем матроида, а
— конечное множество, называемое носителем матроида, а 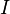 — некоторое множество подмножеств
— некоторое множество подмножеств 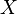 , называемое семейством независимых множеств , то есть
, называемое семейством независимых множеств , то есть 
 . При этом должны выполняться следующие условия:
. При этом должны выполняться следующие условия:
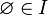
 и
и  , то
, то 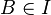
 и мощность A больше мощности B, то существует
и мощность A больше мощности B, то существует 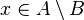 такой, что
такой, что 
Базами матроида называются максимальные по включению независимые множества. Подмножества 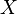 не принадлежащие
не принадлежащие  называются зависимыми множествами. Минимальные по включению зависимые множества называются циклами матроида, это понятие используется в альтернативном определении матроида.
называются зависимыми множествами. Минимальные по включению зависимые множества называются циклами матроида, это понятие используется в альтернативном определении матроида.

Базовое множество E задано векторами a, b, c, d, e, f. Множества с нулевым вектором f и множества, содержащие векторы d и e, линейно зависимы.
Быть тело ,в
а
- векторное пространство и
конечное подмножество . Быть
как набор подмножеств
определено, что в
линейно независимый относительно
являются. Тогда пара
матроид, называемый векторным матроидом.
Например, будьте -Векторное пространство
и в качестве базового количества
даны столбцы следующей матрицы:
Соответствующие векторы-столбцы обозначаются следующим образом:
В результате получается базовая величина и количество
наборов векторов, каждый из которых имеет линейно независимые векторы.
Напротив, векторы находятся в векторном пространстве. линейно зависима, если выполняется одно из следующих условий:
Соответственно, нулевой столбец и скалярные кратные или их индексы в матроиде являются зависимыми.
Для матроида это базы как максимальные по включению элементы
определенный. Для векторного матроида
Это и есть основы векторного пространства . В настоящем примере применяется следующее:
Быть неориентированный мультиграф ( т.е. возможно несколько ребер и петель) с набором узловв
и количество кромокЭ
. Графический матроид
содержит в качестве независимых множеств циклические подграфыГ
.
График является примером с набором узлов
и набор кромок
задано, где ребра определяются следующими мультимножествами :
.
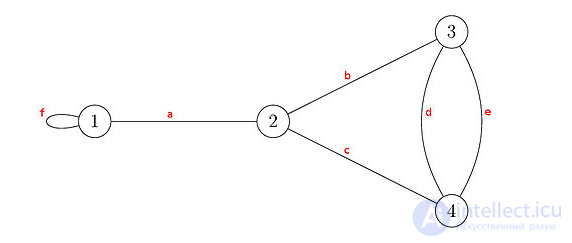
В этом примере круговые подграфы соответствуют независимым наборам .
Базыбграфического матроида соответствуют остовным лесам графа (или остовным деревьям для связных графов). Таким образом, к данному примеру применимо следующее:
.
Матроид — пара  , где
, где 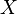 — носитель матроида, а
— носитель матроида, а  — семейство непустых подмножеств
— семейство непустых подмножеств 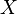 , называемое множеством циклов матроида, для которых выполняются следующие условия:
, называемое множеством циклов матроида, для которых выполняются следующие условия:
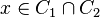 , то
, то 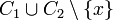 содержит цикл
содержит циклПусть  — частично упорядоченное множество.
— частично упорядоченное множество. 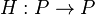 — замыкание в
— замыкание в  , если
, если


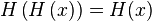
Рассмотрим 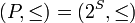 случай, когда частично упорядоченное множество — булева алгебра. Пусть
случай, когда частично упорядоченное множество — булева алгебра. Пусть 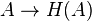 — замыкание
— замыкание 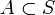 .
.

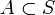 существует такое
существует такое  , что
, что
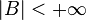
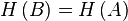
Пара 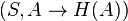 , где
, где 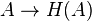 — правильное замыкание на
— правильное замыкание на  , называется матроидом.
, называется матроидом.
Докажем, что в рассмотренном примере множество линейно независимых столбцов действительно является матроидом. Для этого достаточно доказать третье свойство из определения матроида. Проведем доказательство методом от противного.
Доказательство. Пусть A, B ∈ I и |A| = |B| + 1. Пусть W будет пространством векторов, охватываемым A ∪ B . Понятно, что его размерность будет не менее |A|. Предположим, что B ∪ {x} будет линейно зависимо для всех x ∈ A − B (то есть третье свойство не будет выполняться). Тогда B образует базис в пространстве W. Из этого следует, что |A| ≤ dim W ≤ |B|. Но так как по условию A и B состоят из линейно независимых векторов и |A| > |B|, получаем противоречие. Такое множество векторов будет являться матроидом.
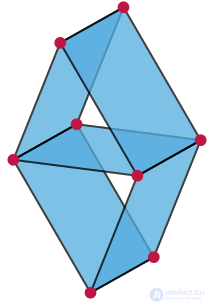
Матроид Вамоса , не линейный ни над каким полем

Матроиды с маленьким числом элементов часто изображают в виде диаграмм. Точки — это элементы основного множества, а кривые «протянуты» через каждую трехэлементную цепь (3-element circuit). Диаграмма показывает 3-ранговый матроид, называемый матроидом Фано, пример, который появился в 1935 в статье Уитни (Whitney).
Из проективной геометрии известно, что матроид Фано непредставим произвольным множеством векторов в вещественном или комплексном векторном пространстве (или в любом векторном пространстве над полем, чьи характеристики отличаются от 2).
 и
и 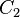 — циклы, то для любого
— циклы, то для любого  содержит цикл
содержит цикл — база и
— база и 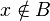 , то
, то  содержит ровно один цикл.
содержит ровно один цикл.
Математик Хасслер Уитни , введший термин «матроид».
Матроиды были представлены и развиты несколькими авторами в 1930-х годах. Целью было аксиоматизировать известные понятия и термины из линейной алгебры , такие как линейная зависимость и независимость , базис и произведение , и перенести их в более общие структурные классы. Это позволило уточнить некоторые понятия в различных областях комбинаторики и сделало чисто комбинаторные вопросы доступными для алгебраических идей и методов. И последнее, но не менее важное: многие соображения теории графов удалось таким образом интегрировать в теорию матроидов.
Как правило, начало теории матроидов приписывают американскому математику Хасслеру Уитни. В 1935 году он исследовал материнских матроидов. , где элементыС
являются строками данной матрицы, и набор строк является независимым, если строки линейно независимы в обычном смысле. Чуть позже Бартель Леендерт ван дер Варден также использовал понятие абстрактной зависимости в своей книге «Современная алгебра». Независимо друг от друга японский математик Такео Накасава в период с 1935 по 1938 год написал четыре статьи, которые делают его сооснователем теории матроида, хотя на долгое время о них забыли.
Кроме того, появились отдельные статьи Гаррета Биркгофа (1935), Сондерса Мак Лейна (1936) и Роберта П. Дилворта (1941–1944) по теоретико-связным и геометрическим аспектам теории матроидов. Рихард Радо работал над комбинаторными приложениями матроидов (1942) и бесконечных матроидов (1949). [ 12 ] Важным стимулом для дальнейшего развития теории матроидов стало поочередное заимствование идей из разных областей и их влияние в других, таких как параллелизм между свойствами размерности в векторных пространствах и ранга в графах . В 1958 и 1959 годах Уильям Томас Тутт опубликовал фундаментальные статьи по матроидам и графам. С тех пор интерес к матроидам и их применениям в комбинаторике неуклонно возрастал, не в последнюю очередь в области комбинаторной оптимизации . Джек Эдмондс и Делберт Рэй Фулкерсон (1965) и Леонид Мирский и Хейзел Перфект (1967) независимо открыли новый класс матроидов, так называемые поперечные матроиды. По словам Уэлша, матроиды оказали на данный момент наибольший эффект в трансверсальной теории (измеряется с точки зрения достигнутых новых результатов и более простых доказательств, найденных для уже известных результатов).
Несколько важных задач комбинаторной оптимизации можно эффективно решить на каждом матроиде. В частности:
Теория бесконечных матроидов намного сложнее теории конечных матроидов и образует самостоятельную тему. Долгое время одной из трудностей было то, что существовало много разумных и полезных определений, ни одно из которых, казалось, не охватывало все важные аспекты теории конечных матроидов. Например, казалось, что сложно объединить базы, контуры и дуальность в одном понятии бесконечных матроидов.
Следующее простейшее бесконечное обобщение — это финитарные матроиды, также известные как предгеометрии . Матроид с возможно бесконечным базовым множеством является финитным, если он обладает свойством
Эквивалентно, каждое зависимое множество содержит конечное зависимое множество.
Примерами являются линейная зависимость произвольных подмножеств бесконечномерных векторных пространств (но не бесконечные зависимости, как в пространствах Гильберта и Банаха ), и алгебраическая зависимость в произвольных подмножествах расширений полей возможно бесконечной степени трансцендентности. Опять же, класс финитарного матроида не является самодвойственным, поскольку двойственный к финитарному матроиду не является финитным.
Конечные бесконечные матроиды изучаются в теории моделей — разделе математической логики , тесно связанном с алгеброй .
В конце 1960-х годов теоретики матроидов запросили более общее понятие, которое разделяет различные аспекты конечных матроидов и обобщает их дуальность. Многие понятия бесконечных матроидов были определены в ответ на этот вызов, но вопрос оставался открытым. Один из подходов, рассмотренных DA Higgs, стал известен как B-матроиды и изучался Higgs, Oxley и другими в 1960-х и 1970-х годах. Согласно недавнему результату Bruhn et al. (2013) , он решает проблему: придя к одному и тому же понятию независимо, они предоставили пять эквивалентных систем аксиом — с точки зрения независимости, базисов, контуров, замыкания и ранга. Дуальность B-матроидов обобщает дуальности, которые можно наблюдать в бесконечных графах.
Аксиомы независимости следующие:
Согласно этим аксиомам, каждый матроид имеет двойственный.
Надеюсь, эта статья про матроид, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое матроид и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.