Лекция
Привет, сегодня поговорим про дерево в теории графов , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дерево в теории графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Лес - упорядоченное множество упорядоченных деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в нее не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведет ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.
Корневое дерево — дерево, в котором выделена одна вершина (корень дерева). Формально корневое дерево определяется как конечное множество  одного или более узлов со следующими свойствами:
одного или более узлов со следующими свойствами:

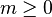 непересекающихся множеств
непересекающихся множеств 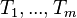 , и каждое из множеств является корневым деревом; деревья
, и каждое из множеств является корневым деревом; деревья 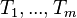 называются поддеревьями данного корня
называются поддеревьями данного корня 
 равен 0;
равен 0; , содержащего данный узел.
, содержащего данный узел.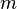 -й ярус дерева
-й ярус дерева  — множество узлов дерева, на уровне
— множество узлов дерева, на уровне 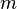 от корня дерева.
от корня дерева.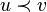 , если вершины
, если вершины 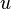 и
и 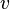 различны и вершина
различны и вершина 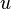 лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной
лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной 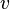 .
.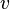 — подграф
— подграф 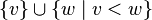 .
.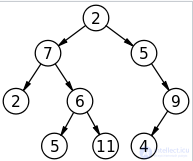
Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (оно же бинарное дерево) имеет несколько значений:
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
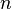 вершинами содержит
вершинами содержит 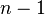 ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда
ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда 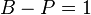 , где
, где  — число вершин,
— число вершин, 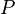 — число ребер графа.
— число ребер графа.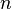 нумерованных вершинах, равно
нумерованных вершинах, равно 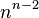 (Теорема Кэли о числе деревьев ).
(Теорема Кэли о числе деревьев ).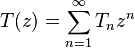
для числа 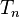 неизоморфных корневых деревьев с
неизоморфных корневых деревьев с 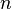 вершинами удовлетворяет функциональному уравнению
вершинами удовлетворяет функциональному уравнению
 .
.
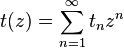
для числа 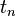 неизоморфных деревьев с
неизоморфных деревьев с 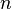 вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
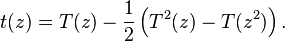
 верна следующая асимптотика
верна следующая асимптотика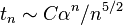
где 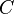 и
и 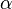 определенные константы,
определенные константы, 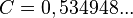 ,
, 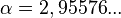 .
.
Дерево можно кодировать наборами из нулей и единиц. Рассмотрим, например, укладку дерева на плоскости. Начиная с какой либо вершины, будем двигаться по ребрам дерева, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах дерева. Проходя по некоторому ребру, записываем 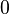 при движении по ребру в первый раз и
при движении по ребру в первый раз и 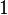 при движении по ребру второй раз (в обратном направлении). Если
при движении по ребру второй раз (в обратном направлении). Если 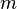 — число ребер дерева, то через
— число ребер дерева, то через 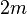 шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из
шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из 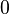 и
и 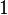 (код дерева) длины
(код дерева) длины 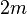 позволяет однозначно восстанавливать не только само дерево
позволяет однозначно восстанавливать не только само дерево 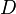 , но и его укладку на плоскости. Произвольному дереву соответствуют несколько таких кодов. В частности, из этого способа кодирования вытекает следующая грубая оценка на число деревьев с
, но и его укладку на плоскости. Произвольному дереву соответствуют несколько таких кодов. В частности, из этого способа кодирования вытекает следующая грубая оценка на число деревьев с 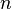 вершинами:
вершинами:
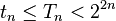
Надеюсь, эта статья про дерево в теории графов , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое дерево в теории графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про дерево в теории графов
Такая кодировка мне понятна, доступна. Учусь кодить. Пишу html графы деревьев.
что значит html графы ?
https://code.sololearn.com/WZTTXNB4wCy1/?ref=app
Наверное, правильнее сказать не графы, а схемы деревьев.
Да, существует большое количество библиотек для визуализации графов,
а вообще т.к понятие граф растяжимое в прямом смысле (один и тот же граф можно изобразить -
визуализировать бесконечным количесвтом образов),
существуют специальные теории и алгоритмы визуализации графов,
например можно прочитать тут
https://intellect.icu/sposoby-vizualizatsii-grafov-silovye-algoritmy-vizualizatsii-grafov-9034
еще есть даже Non-SQL для работы с графами в том числе с визуализацией
вот пример такой БД
http://console.neo4j.org/
https://neo4j.com/
Визуализация гибкого force-directed графа осуществляется с использованием метода численного интегрирования Верле библиотека JS https://github.com/d3/d3
библиотека https://www.graphviz.org/
и другие
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.