Лекция
Привет, Вы узнаете о том , что такое алгоритм вырезания соцветий, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм вырезания соцветий, алгоритм сжатия цветков , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
алгоритм сжатия цветков (англ. Blossom algorithm) — это алгоритм в теории графов для построения наибольших паросочетаний на графах. Алгоритм разработал Джек Эдмондс в 1961 году и опубликовал в 1965 году . Если дан граф G=(V, E) общего вида, алгоритм находит паросочетание M такое, что каждая вершина из V инцидентна не более чем одному ребру из M и |M| максимально. Паросочетание строится путем итеративного улучшения начального пустого паросочетания вдоль увеличивающих путей графа. В отличие от двудольного паросочетания ключевой новой идеей было сжатие нечетного цикла в графе (цветка) в одну вершину с продолжением поиска итеративно по сжатому графу.
Основной причиной, почему алгоритм сжатия цветков важен, является то, что он дал первое доказательство возможности нахождения наибольшего паросочетания за полиномиальное время. Другой причиной является то, что метод приводит к описанию многогранника линейного программирования для многогранника паросочетаний, что приводит к алгоритму паросочетания минимального веса . Как уточнил Александр Схрейвер, дальнейшая важность результата следует из факта, что этот многогранник был первым, доказательство целочисленности которого «не просто следовало из тотальной унимодулярности, а его описание было прорывом в комбинаторике многогранников» .
Если дан граф G=(V, E) и паросочетание M для G, вершина v голая (не покрыта паросочетанием), если нет ребра в M, инцидентного v. Путь в G является чередующейся цепью, если ее ребра попеременно не принадлежат M и содержатся в M. Увеличивающий путь P — это чередующаяся цепь, которая начинается и кончается голыми вершинами. Заметим, что число не принадлежащих паросочетанию вершин в увеличивающем пути больше на единицу числа ребер, принадлежащих паросочетанию, а потому число ребер в увеличивающем пути нечетно. Увеличение паросочетаний вдоль пути P — это операция замены множества M на новое паросочетание .
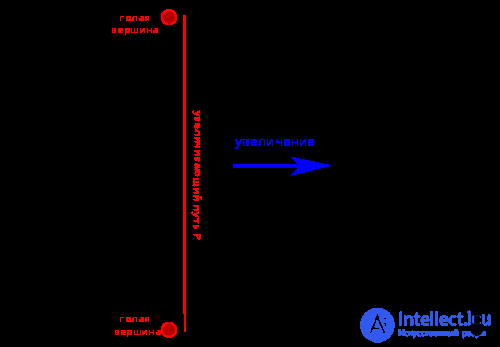
По лемме Бержа, паросочетание M является наибольшим тогда и только тогда, когда нет M-увеличивающего пути в G . Следовательно, либо паросочетание является наибольшим, либо его можно увеличить. Таким образом, начав с некоторого паросочетания, мы можем вычислить наибольшее паросочетание путем увеличения текущего паросочетания с помощью увеличенного пути. Можно формализовать алгоритм следующим образом
ВХОД: Граф G, начальное паросочетание M на G ВЫХОД: наибольшее паросочетание M* на G A1 function найти_наибольшее_паросочетание(G, M) : M* A2найти_увеличивающий_путь(G, M) A3 if P не пустое then A4 return найти_наибольшее_паросочетание(G, увеличиваем M вдоль P) A5 else A6 return M A7 end if A8 end function
Нам нужно описать, каким образом увеличивающие пути могут быть эффективно построены. Подпрограмма их поиска использует цветки и стягивание.
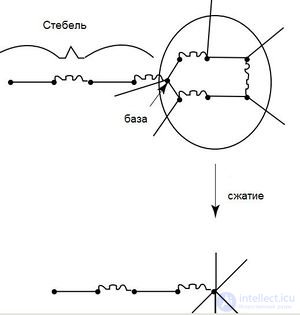
Если дан граф G=(V, E) и паросочетание M графа G, то цветок B — это цикл в G, состоящий из 2k + 1 ребер, из которых в точности k принадлежат M и в котором есть вершина v (база) такая, что существует чередующаяся цепь четной длины (стебель) из v в голую вершину w.
Нахождение цветков:
Определим сжатый граф G’ как граф, полученный из G путем стягивания всех ребер цветка B, и определим сжатое паросточетание M’ как паросочетание графа G’, соответствующее M.
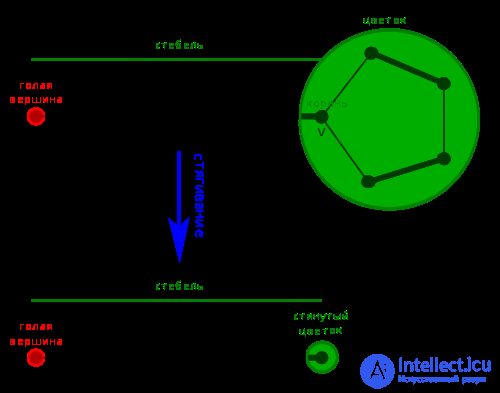
G’ имеет M’-увеличивающий путь тогда и только тогда, когда G имеет M-увеличивающий путь, а тогда любой M’-увеличивающий путь P’ в G’ может быть поднят до M-увеличивающего пути в G путем восстановления цветка B, стянутого ранее, так что сегмент пути P’ (если такой есть), проходящий через vB заменяет на подходящий сегмент, проходящий через B . Более детально:

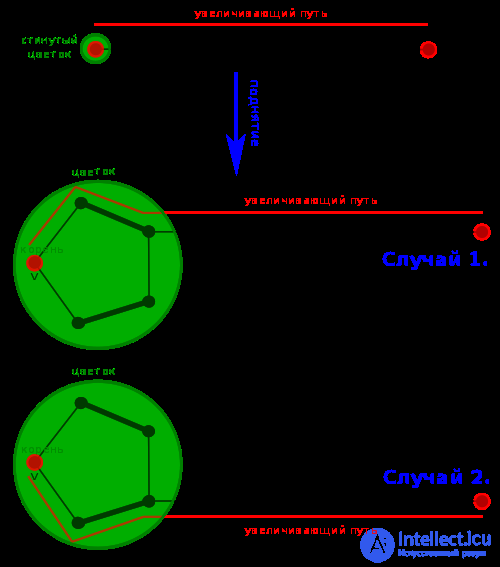
Тогда цветок может быть сжат и поиск может быть продолжен по сжатым графам. Это сжатие является сердцем алгоритма Эдмондса.
Поиск увеличивающего пути использует дополнительную структуру данных, представляющую собой лес F, индивидуальные деревья которого соответствуют порциям графа G. Фактически, лес F тот же самый, что и применяемый для поиска наибольших паросочетаний в двудольных графах (без необходимости стягивания цветков). На каждой итерации алгоритм либо (1) находит увеличивающий путь, либо (2) находит цветок и осуществляет рекурсию в сжатый граф, либо (3) делается вывод, что увеличивающего пути не существует. Дополнительная структура строится посредством инкрементальной процедуры, которая обсуждается ниже .
Процедура построения просматривает вершины v и ребра e графа G и инкрементально обновляет F соответствующим образом. Если v находится в дереве T леса, мы через root(v) обозначим корень дерева T. Если и u, и v лежат в том же дереве T в F, через distance(u, v) обозначим длину единственного пути из u в v в дереве T.
ВХОД: Граф G, паросочетание M в G
ВЫХОД: Увеличивающий путь P в G или пустой путь, если такого пути не найдено
B01 function найти_ увеличивающий_путь(G, M):P
B02  пустой лес
B03 делаем все вершины и ребра непомеченными в G, помечаем все ребра M
B05 for each голой вершины v do
B06 создаем дерево из одной вершины {v} и добавляем дерево в F
B07 end for
B08 while имеется непомеченная вершина v в F с четным distance(v, root(v)) do
B09 while существует непомеченное ребро e={v, w} do
B10 if w не в F then
// w входит в паросочетание, так что добавляем ребро,
// покрывающее e и w в F
B11
пустой лес
B03 делаем все вершины и ребра непомеченными в G, помечаем все ребра M
B05 for each голой вершины v do
B06 создаем дерево из одной вершины {v} и добавляем дерево в F
B07 end for
B08 while имеется непомеченная вершина v в F с четным distance(v, root(v)) do
B09 while существует непомеченное ребро e={v, w} do
B10 if w не в F then
// w входит в паросочетание, так что добавляем ребро,
// покрывающее e и w в F
B11  сочетается с вершиной w в M
B12 добавляем ребра {v,w} и {w,x} в дерево для v
B13 else
B14 if distance(w, root( w )) нечетно then
// не делаем ничего.
B15 else
B16 if root(v) ≠ root(w) then
// Рапортуем о увеличивающем пути в F
сочетается с вершиной w в M
B12 добавляем ребра {v,w} и {w,x} в дерево для v
B13 else
B14 if distance(w, root( w )) нечетно then
// не делаем ничего.
B15 else
B16 if root(v) ≠ root(w) then
// Рапортуем о увеличивающем пути в F  .
B17
.
B17  путь (
путь ( )
B18 return P
B19 else
// Стягиваем цветок в G и ищем путь в сжатом графе.
B20
)
B18 return P
B19 else
// Стягиваем цветок в G и ищем путь в сжатом графе.
B20  цветок, образованный e и ребрами пути
цветок, образованный e и ребрами пути  в T
B21
в T
B21  сжимаем G и M путем стягивания цветка B
B22
сжимаем G и M путем стягивания цветка B
B22  найти_ увеличивающий_путь
найти_ увеличивающий_путь  B23
B23  поднимаем P’ в G
B24 return P
B25 end if
B26 end if
B27 end if
B28 помечаем ребро e
B29 end while
B30 помечаем вершину v
B31 end while
B32 return пустой путь
B33 end function
поднимаем P’ в G
B24 return P
B25 end if
B26 end if
B27 end if
B28 помечаем ребро e
B29 end while
B30 помечаем вершину v
B31 end while
B32 return пустой путь
B33 end function
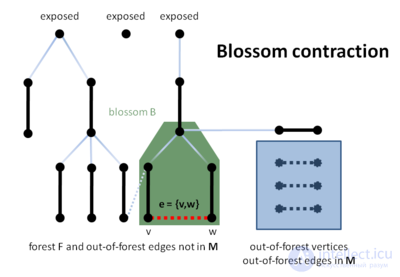
Следующие четыре рисунка иллюстрируют выполнение алгоритма. Об этом говорит сайт https://intellect.icu . Пунктирные линии показывают ребра, которые в этот момент не представлены в лесе. Сначала алгоритм обрабатывает ребро, не принадлежащее лесу, которое приводит к расширению текущего леса (строки B10 — B12).
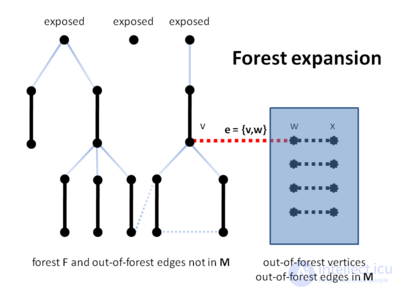
Затем удаляется цветок и сжимается граф (строи B20 — B21).
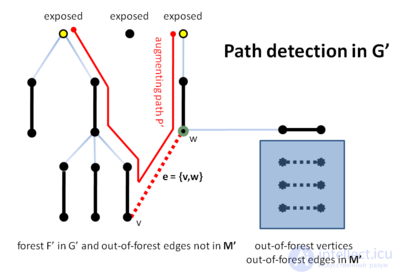
Наконец, алгоритм обнаруживает увеличивающий путь P′ в сжатом графе (строка B22) и поднимает его в исходном графе (строка B23). Заметим, что способность алгоритма стягивания цветков здесь является решающим. Алгоритм не может найти P в исходном графе прямо, поскольку только ребра не из леса между вершинами на четном расстоянии от корня рассматриваются в строке B17 алгоритма.
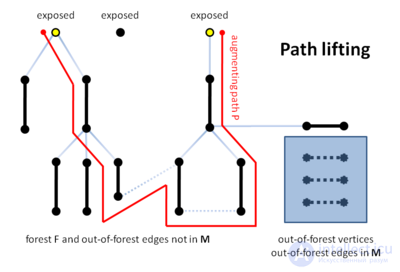
Лес F, построенный функцией найти_увеличивающий_путь(), является чередующимся лесом .
Каждая итерация цикла, начиная со строки B09, либо добавляет вершину в дерево T в F (строка B10), либо находит увеличивающий путь (строка B17), либо находит цветок (строка B20). Легко видеть, что время работы алгоритма равно . Микали и Вазирани[10] показали алгоритм, который строит наибольшее паросочетание за время
.
Алгоритм сводится к стандартному алгоритму для паросочетаний в двудольных графах , если G является двудольным. Поскольку в этом случае нет нечетных циклов G, цветки никогда не будут найдены и можно просто удалить строки B20 — B24 алгоритма.
Задачу о паросочетаниях можно обобщить назначением весов ребрам графа G. В этом случае задается вопрос о множестве M, которое дает паросочетание с максимальным (минимальным) полным весом. Взвешенную задачу о паросочетаниях можно решить с помощью комбинаторного алгоритма, который использует невзвешенный алгоритм Эдмондса в качестве подпрограммы . Владимир Колмогоров дал эффективную имплементацию этого алгоритма на C++[11].
Рассмотрим неориентированный невзвешенный граф G=⟨V,E⟩, где V — множество вершин, E — множество ребер. Требуется найти в нем максимальное паросочетание.
Приведем пример, на котором алгоритм Куна работать не будет. Рассмотрим граф G с множеством вершин V=1,2,3,4, и множеством ребер —E=⟨1,2⟩,⟨2,3⟩,⟨3,1⟩,⟨2,4⟩ и пусть ребро ⟨2,3⟩ взято в паросочетание. Тогда при запуске из вершины 1, если обход пойдет сначала в вершину 2, то он зайдет в тупик в вершине 3, вместо того чтобы найти увеличивающую цепь 1−3−2−4. Как видно на этом примере, основная проблема заключается в том, что при попадании в цикл нечетной длины, обход может пойти по циклу в неправильном направлении.
| Теорема: |
|
Пусть даны граф G, паросочетание M в G и цикл Z длины 2k+1, содержащий k ребер паросочетания M и вершинно непересекающийся с остальными ребрами из M. Построим новый граф G′ из графа G, сжимая цикл Z до единичной вершины, при этом все ребра, инцидентные вершинам этого цикла, становятся инцидентными вершине в новом графе. Тогда паросочетание M−E(Z), где E(z) — ребра, инцидентные циклу, является наибольшим в G′ тогда и только тогда, когда М — наибольшее паросочетание в G
|
| Доказательство: |
| ▹ |
|
Предположим, что M не является наибольшим паросочетанием в G, тогда в силу теоремы о максимальном паросочетании и дополняющих цепях существует увеличивающая относительно M цепь P. Если P не пересекается с Z, то цепь является увеличивающей относительно M′ и в графе G′, а значит, M′ не может быть наибольшим паросочетанием. Поэтому предположим, что цепь P пересекается с Z. Заметим, что хотя бы одна концевая вершина цепи P не лежит на Z, обозначим ее через u. Тогда пройдем по цепи P, начиная с u до первой встречной вершины на Z, обозначим ее через v. Тогда, при сжатии цикла Z, участок P[u,v] отобразится на увеличивающую цепь относительно M′, то есть M′ не является максимальным паросочетанием, что противоречит нашему предположению. Теперь допустим, что M′ не является наибольшим паросочетанием в графе G′. Обозначим через N′ паросочетание в G′, мощности большей, чем M′. Восстановим граф G, тогда N′ будет соответствовать некоторому паросочетанию в G, покрывающему не более одной вершины в Z. Следовательно паросочетание N′ можно увеличить, используя k ребер цикла Z, и получить паросочетание N, размера |N|=|N′|+k>|M′|+k=|M|, то есть M не является наибольшим паросочетанием в G, приходим к противоречию. Таким образом теорема доказана. |
| ◃ |
Для простоты описания алгоритма введем некоторые определения.
| Определение: |
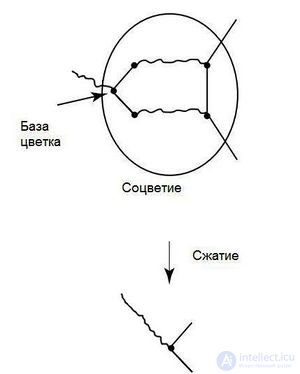
| Будем называть соцветием B графа G его цикл нечетной длины.
Cжатием соцветия назовем граф G′, полученный из G сжатием всего нечетного цикла в одну псевдо-вершину. Все ребра, инцидентные вершинам этого цикла, становятся инцидентными псевдо-вершине в новом графе. База соцветия - вершина соцветия, в которую входит ребро не из данного соцветия. |
Опишем алгоритм, позволяющий находить максимальное паросочетание для произвольного графа G. Из теоремы Эдмондса понятно, что необходимо рассматривать паросочетание в сжатом графе, где его можно найти, к примеру, при помощи алгоритма Куна, а после восстанавливать паросочетание в исходном графе.
Основную сложность представляют операции сжатия и восстановления цветков. Чтобы эффективно это делать, для каждой вершины необходимо хранить указатель на базу цветка, которому она принадлежит, или на себя в противном случае. Предположим, что для поиска паросочетаний в сжатом графе, мы используем обход в ширину. Тогда на каждой итерации алгоритма будет строиться дерево обхода в ширину, причем путь в нем до любой вершины будет являться чередующимся путем, начинающимся с корня этого дерева. Будем класть в очередь только те вершины, расстояние от корня до которых в дереве путей четно. Также для каждой вершины, расстояние до которой нечетно, в массиве предков p[] необходимо хранить ее предка — четную вершину. Заметим, что если в процессе обхода в ширину мы из текущей вершины v приходим в такую вершину u, что она является корнем или принадлежит паросочетанию и дереву путей, то обе эти вершины принадлежат некоторому цветку. Действительно, при выполнении этих условий эти вершины являются четными вершинами, следовательно расстояние от них до их наименьшего общего предка имеет одну четность. Найдем наименьшего общего предка lca(u,v) вершин u, v, который является базой цветка. Для нахождения самого цикла необходимо пройтись от вершин u, v до базы цветка. В явном виде цветок сжимать не будем, просто положим в очередь обхода в ширину все вершины, принадлежащие цветку. Также для всех четных вершин (за исключением базы) назначим предком соседнюю вершину в цикле, а для вершин u и v назначим предками друг друга. Это позволит корректно восстановить цветок в случае, когда при восстановлении увеличивающего пути мы зайдем в нечетную вершину цикла.
Всего имеется V итераций, на каждой из которых выполняется обход в ширину за O(E), кроме того, могут происходить операции сжатия цветков — их может быть O(V). Сжатие соцветий работает за O(V), то есть общая асимптотика алгоритма составит O(V(E+V2))=O(V3).
пиши/читай в комментариях
стягивание ребра , отождествление вершин ,
Исследование, описанное в статье про алгоритм вырезания соцветий, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое алгоритм вырезания соцветий, алгоритм сжатия цветков и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.