Лекция
Привет, сегодня поговорим про путь в теории графов , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое путь в теории графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Путь в графе — последовательность вершин, имеющая для каждой вершины ребро, соединяющее ее со следующей вершиной в последовательности.
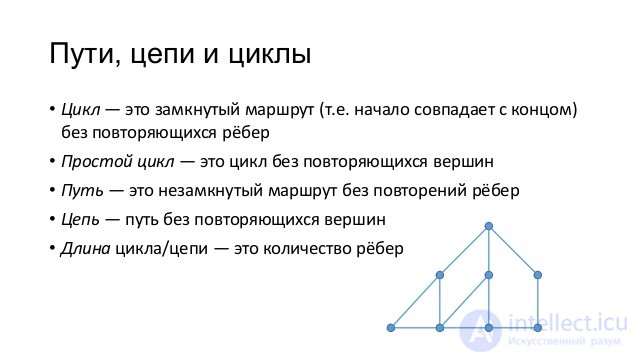
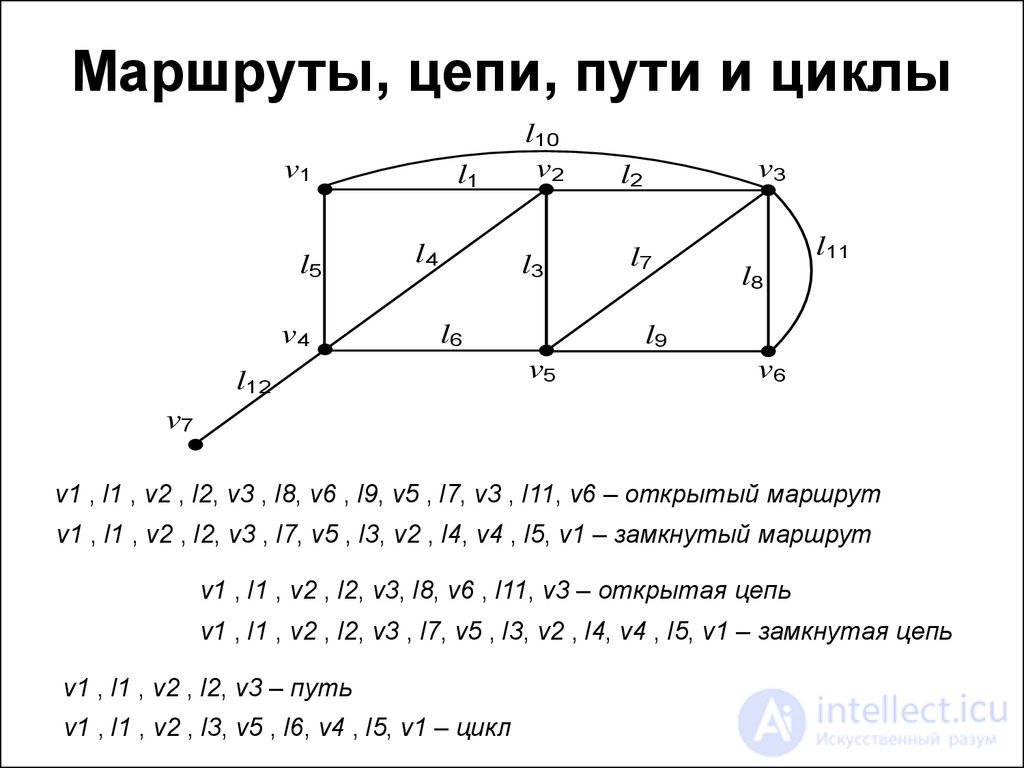
Пусть G - неориентированный граф. Путем в G называется такая конечная или бесконечная последовательность ребер и вершин 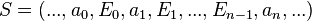 ,
,
что каждые два соседних ребра 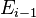 и
и 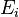 имеют общую вершину
имеют общую вершину  .
.
Таким образом, можно написать 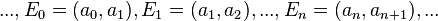
Отметим, что одно и тоже ребро может встречаться в пути несколько раз. Если нет ребер, предшествующих  , то
, то 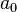 называется начальной вершиной S, а если нет ребер, следующих за
называется начальной вершиной S, а если нет ребер, следующих за  , то
, то 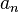 называется конечной вершиной S. Об этом говорит сайт https://intellect.icu . Любая вершина, принадлежащая двум соседним ребрам называется внутренней. Так как ребра и вершины в пути могут повторяться, внутренняя вершина может оказаться начальной или конечной вершиной.
называется конечной вершиной S. Об этом говорит сайт https://intellect.icu . Любая вершина, принадлежащая двум соседним ребрам называется внутренней. Так как ребра и вершины в пути могут повторяться, внутренняя вершина может оказаться начальной или конечной вершиной.
Если начальная и конечная вершины совпадают, путь называется циклическим. Путь называется цепью, а циклический путь - циклом, если каждое его ребро встречается не более одного раза (вершины могут повторяться). Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется. Цикл с концом 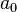 называется простым циклом, если
называется простым циклом, если 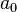 не является в нем промежуточной вершиной и никакие другие вершины не повторяются.
не является в нем промежуточной вершиной и никакие другие вершины не повторяются.
К сожалению, эта терминология не устоялась. Уилсон пишет: «То, что мы назвали маршрутом, называют также путем, реберной последовательностью. Цепь называют путем, полупростым путем; простую цепь – цепью, путем, дугой, простым путем, элементарной цепью; замкнутую цепь – циклической цепью, контуром; цикл – контуром, контурной цепью, простым циклом, элементарным циклом.»

Ориентированный цикл. Без стрелок это просто цикл. Это не простой цикл, поскольку синие вершины используются дважды.
Пути, цепи и циклы являются фундаментальными концепциями теории графов и определяются во вводной части большинства книг по теории графов. Смотрите, например, Бонди и Марти (Bondy, Murty, 1976), Гиббонс (Gibbons, 1985), или Дистель (2005).
Путь, для которого никакие ребра графа не соединяют две вершины пути называется индуцированным путем.
Простая цепь, содержащая все вершины графа без повторений известна как Гамильтонов путь.
Простой цикл, содержащий все вершины графа без повторений известен как Гамильтонов цикл.
Цикл, получаемый добавлением ребра графа к остовному дереву исходного графа известен как Фундаментальный цикл.
Два пути вершинно независимы, если они не имеют общих внутренних вершин. Аналогично два пути реберно независимы, если они не имеют общих внутренних ребер.
Длина пути — это число ребер, используемых в пути, при этом многократно используемые ребра считаются соответствующее число раз. Длина может равняться нулю, если путь состоит из одной только вершины.
Взвешенный граф ставит в соответствие каждому ребру некоторое значение (вес ребра). Весом пути во взвешенном графе называется сумма весов ребер пути. Иногда вместо слова вес употребляется цена или длина.
На этом все! Теперь вы знаете все про путь в теории графов , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое путь в теории графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про путь в теории графов
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.