7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ

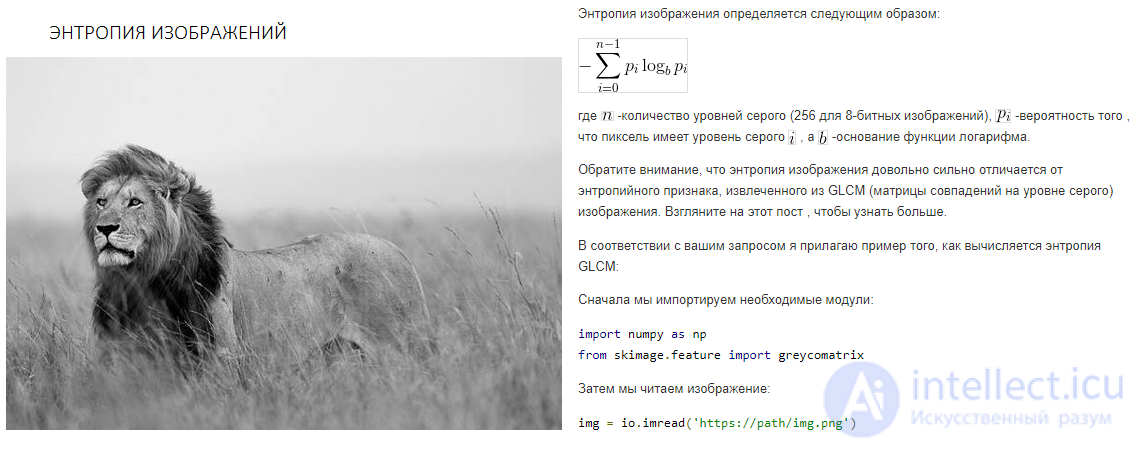
Привет, Вы узнаете о том , что такое энтропия изображений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энтропия изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Информационная энтропия — мера неопределенности некоторой системы (в статистической физике или теории информации), в частности, непредсказуемость появления какого-либо символа первичного алфавита. В последнем случае при отсутствии информационных потерь энтропия численно равна количеству информации на символ передаваемого сообщения.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределенность появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии {\displaystyle n}-го порядка, см. ниже) встречаются очень редко, то неопределенность уменьшается еще сильнее.

Энтропия изображения определяется следующим образом:

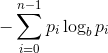
где 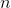-количество уровней серого (256 для 8-битных изображений), 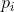-вероятность того , что пиксель имеет уровень серого 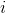, а 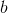-основание функции логарифма.

Обратите внимание, что энтропия изображения довольно сильно отличается от энтропийного признака, извлеченного из GLCM (матрицы совпадений на уровне серого) изображения. Взгляните на этот пост , чтобы узнать больше.

В соответствии с вашим запросом я прилагаю пример того, как вычисляется энтропия GLCM:

Сначала мы импортируем необходимые модули:

import numpy as np
from skimage.feature import greycomatrix

Затем мы читаем изображение:

img = io.imread('https://path/img.png')

GLCM (соответствующий пикселю справа ) изображения выше вычисляется следующим образом:

glcm = np.squeeze(greycomatrix(img, distances=[1], 
                               angles=[0], symmetric=True, 
                               normed=True))

И, наконец, мы применяем эту формулу для вычисления энтропии:

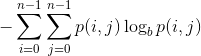
где 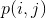представляет записи GLCM.

Если мы установим 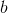в 2, результат будет выражен в битах .

entropy = -np.sum(glcm*np.log2(glcm + (glcm==0)))
# yields 10.7040625

Очевидно, что одни изображения являются более содержательными, чем другие, т. Об этом говорит сайт https://intellect.icu . е. имеют больше деталей или при анализе из них удается извлечь больше данных. Детали, данные и другие подобные понятия являются качественными и довольно расплывчатыми. Поэтому часто бывает необходимо ввести количественные характеристики изображения, позволяющие оценивать предельные свойства алгоритмов кодирования, исправления и анализа изображений. Один из подходов к количественному описанию изображений состоит в применении теории информации [39-42].

Согласно методике, описанной в разд. 5.3, допустим, что матрица 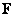размера 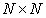, составленная из квантованных отсчетов изображения, будет заменена вектор-столбцом 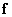размера 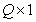(где 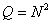), полученным путем развертки матрицы 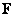по столбцам. В принципе такие векторы можно рассматривать как изображения на выходе некоторого источника, который может генерировать любой из возможных векторов. В одном из крайних случаев получается темное изображение с минимальной яркостью всех элементов, а в противоположном случае — изображение с максимальной яркостью. Между этими крайними случаями заключено множество различных изображений. Если яркость каждого из 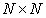элементов изображения квантуется на 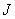уровней, то данный источник может создать 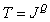различных изображений. Многие из них имеют хаотическую структуру и похожи на реализации двумерного случайного шума. Лишь очень небольшое число из 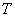возможных изображений будут такими, какие дал бы реальный датчик при наблюдении за окружающим миром. В принципе можно считать, что имеется априорное распределени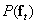е (где 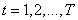) вероятности появления каждого из возможных состояний вектора 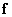. Измерить или промоделировать это распределение очень непросто, но сама идея в конце концов приводит к полезным результатам.

В 1948 г. Шеннон [39] опубликовал свою знаменитую книгу «Математическая теория связи», в которой был дан способ количественного описания свойств источников данных и систем передачи информации. В основе шенноновской теории информации лежит понятие об энтропии. При векторном описании изображения среднее количество информации в изображении равно энтропии источника:

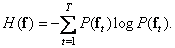(7.6.1)

В данном определении энтропии применяются логарифмы с основанием два и энтропия измеряется в двоичных единицах. Энтропию источника полезно знать при кодировании изображений, поскольку согласно теореме о кодировании при отсутствии помех [39], теоретически можно закодировать без искажений изображения, создаваемые источником с энтропией 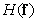, затратив на кодирование 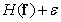двоичных единиц, где 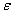— бесконечно малая положительная величина. И наоборот, в принципе невозможно закодировать изображения без искажений, если число двоичных единиц меньше чем .

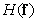Вероятность появления 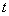-го вектора, описывающего изображение, можно выразить через совместное распределение вероятностей уровней яркости элементов изображения

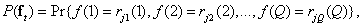(7.6.2)

где 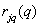— значение 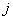-го уровня квантования для 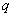-гo элемента. Эту вероятность можно выразить также в виде произведения условных вероятностей:

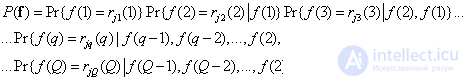. (7.6.3)

Логарифмируя обе части равенства (7.6.3) по основанию два и учитывая определение энтропии (7.6.1), получаем

. (7.6.4)

В равенстве (7.6.4) 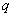-e слагаемое, обозначенное через 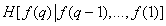, можно рассматривать как выражение для средней информации, содержащейся в 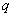-й компоненте вектор-изображения 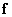, при условии, что точно известны яркости предшествующих 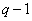компонент. Таким образом,

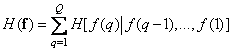. (7.6.5)

Это выражение, описывающее энтропию источника изображений, является общим и не зависит от того, в каком порядке берутся элементы изображения. Рассмотрим теперь вид формулы (7.6.5) для двух случаев: 1) изображение развертывается по столбцам и 2) когда все элементы изображения поступают одновременно. Можно показать, что при развертке изображения по столбцам

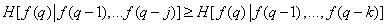, (7.6.6)

где 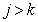. Это означает, что информация, содержащаяся в 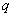-й точке, с увеличением числа полностью известных предшествующих элементов изображения в среднем только уменьшается. Равенство обеих частей соотношения (7.6.6) достигается только тогда, когда яркости всех элементов распределены независимо. Если количество известных предшествующих элементов неограниченно увеличивается, то правая часть неравенства (7.6.6) стремится к некоторому ненулевому предельному значению, обозначаемому как .

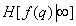Если пренебречь малосущественными для достаточно крупных изображений краевыми эффектами, то энтропию изображения можно приближенно выразить в виде

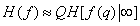. (7.6.7)

Таким образом, можно считать, что энтропия всего изображения равна предельному значению условной энтропии одного элемента изображения, умноженному на полное число элементов.

В системах с разверткой изображения предельная условная энтропия определяется на основе конечной последовательности предыдущих элементов. Так, если этих элементов был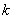о , то

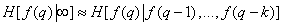. (7.6.8)

В явной форме

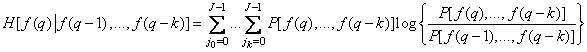, (7.6.9)

где совместное распределение вероятностей

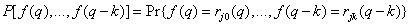(7.6.10)

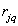( — уровни квантования яркости). Для вычисления условной энтропии (7.6.9) необходимо либо ввести модель совместного распределения вероятностей, либо измерить соответствующие распределения частот для изображения или некоторого класса изображений.

Таблица 7.6.1. Оценки энтропии изображения, полученные Шрайбером

Порядок	Функциональное выражение энтропии	Энтропия, бит/элемент
Первый		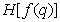4,4
Второй		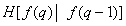1,9
Третий		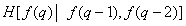1,5

Шрайбер [43] оценил энтропию первого, второго и третьего порядка для нескольких изображений, квантованных на 64 уровня, измеряя распределения относительных частот того же порядка. Полученные распределения были подставлены в формулу (7.6.10) вместо соответствующих распределений вероятностей. При таком способе измерений предполагается, что источник изображений является стационарным и эргодическим, т. е. усреднение по ансамблю изображений можно заменить усреднением по отдельному изображению. Результаты измерений, проведенных Шрайбером для конкретного изображения, приведены в табл. 7.6.1. Для кодирования этого изображения с помощью обычной ИКМ требуются шестиразрядные кодовые слова, т. е. затрачивается 6 бит/элемент. Теоретически для его кодирования достаточно 4,4 бит/элемент при условии, что все элементы кодируются по отдельности. Если же использовать значение предыдущего элемента, то теоретический предел уменьшится до 1,9 бит/элемент. Иначе говоря, предыдущий элемент дает 2,5 бита информации об элементе 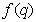. Учет еще одного предшествующего элемента дает всего 0,4 бита дополнительной информации. Таким образом, оказалось, что в данном изображении большая часть дополнительно извлекаемой информации содержится в небольшом числе предыдущих элементов.

Выше был описан метод оценки энтропии изображения, развернутого по столбцам, при котором предельная условная энтропия 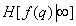аппроксимируется условной энтропией, вычисленной с учетом нескольких предыдущих элементов в том же столбце. Такой метод можно применить для оценки энтропии изображения, когда все его элементы поступают одновременно.

Допустим, что 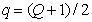обозначает номер центрального элемента вектора 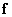с нечетным числом элементов. Тогда совместное распределение вероятностей можно представить в виде

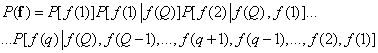(7.6.11)

Повторяя рассуждения, которые привели к соотношению (7.6.7), энтропию источника изображений можно выразить приближенным равенством

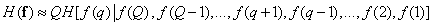. (7.6.12)

Полученное «двустороннее» выражение для условной энтропии можно в свою очередь аппроксимировать, учитывая только ближайшие элементы столбца:

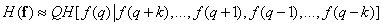. (7.6.13)

Развивая эту идею, можно включить в выражение для оценки энтропии все элементы вектора, которые имеют достаточно сильные статистические связи с 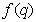. Во многих случаях такие элементы оказываются геометрически ближайшими к исследуемому. Поэтому можно принять следующую оценку энтропии:

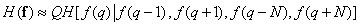, (7.6.14)

где 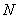— длина столбца, а энтропия элемента 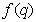определяется значениями ближайших четырех элементов, находящихся сверху, снизу, справа и слева от него.

Прейс [44] вычислял энтропию двухградационных факсимильных документов, используя несколько предшествующих элементов развертки. К сожалению, из-за чрезмерного объема необходимых вычислений трудно оценить энтропию многоградационных изображений даже с использованием упрощенной формулы (7.6.14). Для вычислений по этой формуле необходимо получить распределение частот пятого порядка, причем число возможных значений каждого аргумента равно числу уровней квантования яркости. Приходится делать печальный вывод, что вычисление энтропии в принципе позволяет оценивать «содержательность» изображения, однако для многоградационных изображений такие вычисления практически невыполнимы.

Вау!! 😲 Ты еще не читал? Это зря!

• Дифференциальная энтропия ( энтропия для непрерывного распределения)
• Взаимная информация
• Энтропийное кодирование
• Цепь Маркова
• Расстояние Кульбака — Лейблера

Выводы из данной статьи про энтропия изображений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое энтропия изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений