4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ

Привет, сегодня поговорим про эффекты связанные с наложением спектров, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое эффекты связанные с наложением спектров , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Для безошибочного восстановления непрерывного изображения необходимо ограничить ширину спектра исходного изображения, взять отсчеты по пространственным переменным с частотой не ниже найквистовской и интерполировать отсчеты изображения. Вопрос об интерполяции рассмотрен в следующем разделе, а здесь дан анализ эффектов, возникающих при дискретизации с недостаточной частотой.

Если при такой дискретизации имеет место наложение спектров, как отмечено штриховкой на рис. 4.2.3, то в восстановленное изображение будут внесены ложные пространственные гармоники [11, 12]. На рис. 4.2.4 показано, как выглядят на реальном изображении ошибки, вызванные наложением спектров. Недостаточная частота дискретизации приводит к появлению в восстановленном изображении ложных низкочастотных гармоник. В оптике это явление называют муаровыми узорами или муар-эффектом.

Согласно равенству (4.1.7), спектр дискретизованного изображения можно представить виде

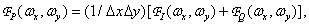     (4.2.12)

где 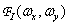 описывает спектр исходного изображения, дискретизованного с периодом 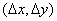. Слагаемое

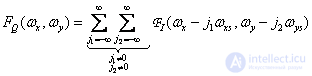     (4.2.13)

описывает те компоненты спектра дискретизованного изображения, которые получаются при повторении исходного спектра с периодам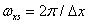и  и .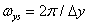

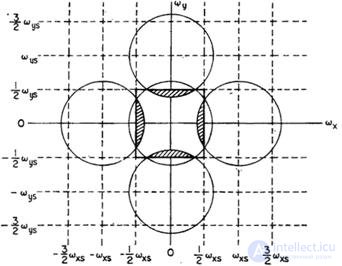
Рис. 4.2.3. Спектры двумерной функции, дискретизованной с недостаточной частотой.

При отсутствии наложения спектров оптимальную интерполяцию отсчетов изображения можно получить, пропуская дискретизованное изображение через идеальный фильтр нижних частот с частотной характеристикой

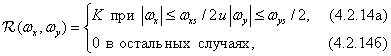
где 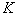 - нормирующая постоянная. Если этот же метод применить для восстановления изображения, дискретизованного с недостаточной частотой, то получится изображение, описываемое функцией

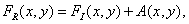     (4.2.15)

где слагаемое

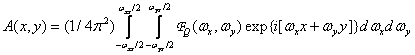     (4.2.16)

соответствует деталям восстановленного изображения, которые появились вследствие наложения. Все коэффициенты, изменяющие амплитуду, входят в .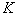

4.2.4. Пример искажений, вызванных наложением спектров: а - исходное изображение; б – дискретизованное изображение.

Ложную компоненту (4.2.16) можно существенно ослабить, если для интерполяции применить фильтр, частотная характеристика которого согласована со спектром исходного изображения. Этот метод описан в гл. 15. Ниже будет рассмотрен другой подход, при котором для уменьшения наложения спектров изображение перед дискретизацией подвергают низкочастотной фильтрации.

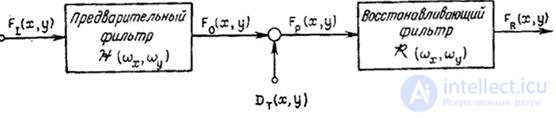
Рис. 4.2.5. К анализу ошибок, вызванных наложением спектров.

На рис. 4.2.5 представлена модель, служащая для количественного анализа эффектов, связанных с наложением спектров. Об этом говорит сайт https://intellect.icu . В ней предполагается, что исходное изображение 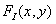 является реализацией двумерногослучайного процесса с известной спектральной плотностью 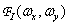. Исходное изображение пропускают через предварительный линейный пространственный фильтр с частотной характеристикой 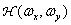. Будем полагать, что этот фильтр обеспечивает плавное ослабление высших пространственных гармоник (т. е. это не идеальный фильтр нижних частот с резкой отсечкой). Затем отфильтрованное изображение дискретизируется с шагом  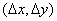с помощью идеального пространственного дискретизатора. Далее отсчеты интерполируются в восстанавливающем фильтре и получается копия исходной) изображения. Согласно равенству (1.10.8), спектральная плотностьизображения на выходе предварительного фильтра равна

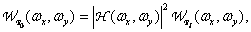                          (4.2.17)

а спектр дискретизованного изображения

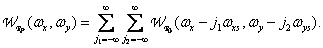     (4.2.18)

Желательно разделить эффекты, вызванные дискретизацией с недостаточной частотой, и последствия неточного восстановления. Поэтому здесь будем полагать, что в качестве восстанавливающего фильтра взят оптимальный фильтр с частотной характеристикой (4.2.14). Мощность компоненты сигнала при 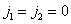 проходящей через такой фильтр, при этом равна

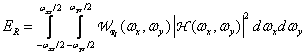     (4.2.19)

В идеальном случае частотная характеристика предварительного фильтра должна совпадать с частотной характеристикой (4.2.14) восстанавливающего фильтра. При этом мощность дискретизованного сигнала оказывается наибольшей и равна

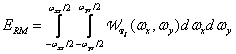                               (4.2.20)

Уменьшение резкости изображения, связанное с введением предварительного фильтра, можно выразить отношением

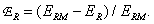                                                          (4.2.21)

Ошибку, вызванную наложением спектров, обычно определяют через энергию паразитных гармоник, принадлежащих смещенным спектрам, попадающим в полосу пропускания восстанавливающего фильтра. Предположим для упрощения, что частота дискретизации довольно высока и вклад спектров, смещенных на 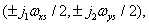 пренебрежимо мал пр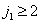и  и 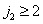. Полная энергия ошибки, вызванной наложением спектров (см. заштрихованные участки на рис. 4.2.3), равна

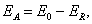                                                                               (4.2.22)

где

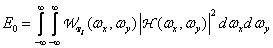                   (4.2.23)

есть энергия сигнала на выходе предварительного фильтра. Тогда ошибку из-за наложения спектров можно определить как [11]

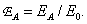                                                                                 (4.2.24)

Эту ошибку можно уменьшить путем ослабления высших пространственных гармоник 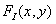 в предварительном фильтре. Однако любое ослабление гармоник, попадающих в полосу пропускания восстанавливающего фильтра, приводит к ухудшению резкости изображения. Таким образом, приходится идти на компромисс между резкостью дискретизованного изображения и ошибкой, вызванной наложением спектров.

Рассмотрим теперь соотношение между величиной этой ошибки и степенью снижения резкости применительно к нескольким типам предварительных фильтров, вероятно, простейшим способом пространственнойфильтрации изображения, полученного в некогерентном свете, является пропускание изображения через линзу с ограниченной апертурой. Пространственную фильтрацию также можно осуществить, дефокусируя оптическую систему. На рис. 13.2.2 показана зависимость частотной характеристики круглой линзы от степени ее дефокусировки. Даже при использовании точно сфокусированной линзы, не имеющей аберраций, получается некоторое смазывание изображения из-за дифракции на конечной апертуре. Частотная характеристикабезаберрационной круглой линзы диаметром 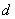, вносящей только дифракционные искажения, равна [13, стр. 83]

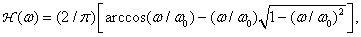
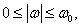       (4.2.25а)

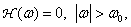                                                                                                                 (4.2.25б)

где 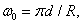 а 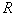 - расстояние от линзы до фокальной плоскости. В предыдущем разделе было отмечено, что неидеальная дискретизация, когда ширина дискретизирующего импульса конечна, эквивалентна идеальной дискретизации того же изображения, но пропущенного через пространственный фильтр, импульсный откликкоторого (после изменения направления обеих координатных осей) совпадает с формой дискретизирующего импульса. Таким образом, дискретизирующий импульс может производить предварительную фильтрацию.

В некогерентной оптической системе сканирующего микроденситометра дискретизирующий импульс имеет прямоугольную форму:

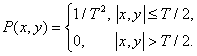      (4.2.26)

Частотная характеристика в этом случае равна

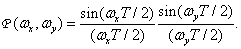     (4.2.27)

В электронно-лучевых трубках образуется световое пятно с двумерным гауссовым распределением яркости.

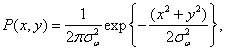     (4.2.28)

где 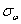 характеризует ширину луча. Частотная характеристика сканирующей системы с гауссовым пятном имеет вид

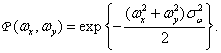     (4.2.29)

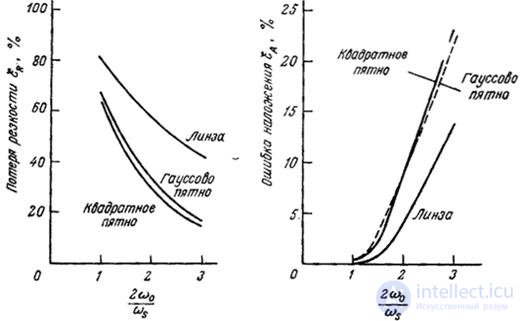
Рис. 4.2.6. Ошибка, вызванная наложением спектров, и потеря резкости для различных предварительных фильтров при .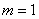

На рис. 4.2.6 приведены графики зависимости потери резкости и величины ошибки, вызванной наложением спектров, от 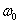 для безаберрационной линзы, а также для квадратного и гауссова пятен. Ширина квадратного пятна выбрана равной 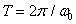, так что первый нуль функции  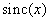совпадает с частотой отсечкичастотной характеристики линзы. Рассеяние гауссова пятна выбрано равным 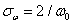. В данном примере спектр исходного изображения моделировался функцией

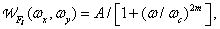     (4.2.30)

где 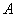 - амплитудный множитель,  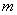- целочисленный параметр, определяющий скорость, с которой амплитуда спектра уменьшается с ростом частоты, а  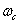- пространственная частота, на которой амплитуда спектра уменьшается в два раза. Кривые, приведенные на рис. 4.2.6, показывают, что предварительная фильтрация, осуществляемая при гауссовой и квадратной формах сканирующего пятна, дает примерно одинаковые результаты, а безаберрационная линза с конечной апертурой при той же величине ошибки, вызванной наложением спектров, дает несколько большую потерю резкости. При использовании дефокусированной линзы получаются самые плохие результаты.

Надеюсь, эта статья об увлекательном мире эффекты связанные с наложением спектров, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое эффекты связанные с наложением спектров и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений