11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ

Привет, Вы узнаете о том , что такое рекурсивная фильтрация, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое рекурсивная фильтрация , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

В предыдущих разделах данной главы обработка с преобразованием рассматривалась как косвенный метод выполнения двумерной линейной обработки. Было показано, что для обработки с преобразованием часто требуется гораздо меньше арифметических операций, чем при использовании стандартных методов. В данном разделе будет рассмотрен другой способ линейной обработки, называемый рекурсивной фильтрацией [14-16]. Иногда рекурсивная фильтрация оказывается даже более эффективной, чем обработка с преобразованием. Кроме того, в этом случае для хранения данных требуется ЗУ меньшей емкости, чем при обработке с преобразованием.

Рекурсивная фильтрация основывается на рекуррентном соотношении между входными и выходными переменными системы. Для одномерных сигналов подобное рекуррентное соотношение имеет следующий вид [14]:

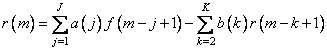,                       (11.6.1)

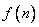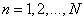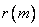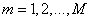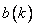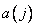где ,  - отсчеты входной последовательности, ,  - отсчеты выходной последовательности, а  и  - весовые множители. Ключевой момент здесь в том, что -й элемент выходной последовательности зависит не только от последнего и 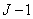 предпоследних элементов входной последовательности, но и от  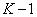предыдущих элементов выходной последовательности.

Большинство методов синтеза и анализа рекурсивных фильтров основано на применении 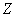-преобразования. По определению [17, 18] 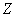-преобразование 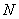-элементной последовательности  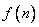дает образ

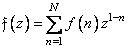.              (11.6.2)

Нетрудно показать, что 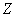-преобразование выражения (11.6.1) дает образ

,                  (11.6.3)

гд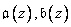е  и  - образы соответствующих последовательностей.

Двумерная рекурсивная фильтрация основана на следующем рекуррентном соотношении между входным и выходным массивами [19, 20]:

               (11.6.4)

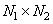где  - входной массив из  элементов,  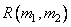- выходной массив из  элементов, а 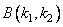 и  - весовые множители. Об этом говорит сайт https://intellect.icu . Предполагается, что процесс рекурсивной фильтрации начинается с левого верхнего угла входного массива. С помощью двумерного 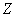-преобразования из равенства (11.6.4) получается

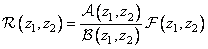,                  (11.6.5)

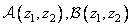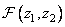где  и  - двумерные образы соответствующих массивов. Так, например,

.               (11.6.6)

При синтезе рекурсивных фильтров требуется выбрать такие массивы весовых множителе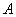й  и 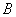, чтобы выходной массив  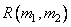оказался эквивалентным массиву, получаемому в результате свертки функции , описывающей исходное изображение, с заданным импульсным откликом 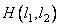. Как правило, точного совпадения массивов добиться не удается и при синтезе фильтров приходится пользоваться приближенными методами [21, 22]. При этом возникает вопрос об устойчивости рассчитанного рекурсивного фильтра. Если фильтр неустойчив, то ошибки округления или шум, присутствующий во входном массиве, могут в ходе обработки не ослабляться, а увеличиваться до очень большого уровня. Рекурсивный фильтр устойчив [20], если коэффициенты  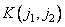разложения частотной характеристики фильтра в ряд по степеням переменных  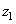и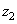 

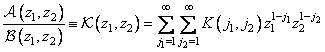             (11.6.7)

являются абсолютно суммируемыми, т. е. удовлетворяют условию

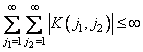.                      (11.6.8)

Разработано несколько методов проверки рекурсивных фильтров на устойчивость [23-25]. При обработке изображения согласно равенству (11.6.4) требуется выполнить

                (11.6.9)

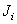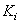арифметических операций. Здесь  и  - размеры массивов весовых множителей для входного и выходного изображений, a  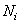- размеры входного изображения. Если изображения и массивы весовых множителей - квадратные (т. е. 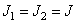,  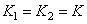и 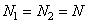), то при рекурсивной фильтрации нужно выполнить

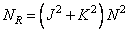               (11.6.10)

операций. Для сравнения укажем, что для получения конечной свертки (см. разд. 9.3) требуется

                (11.6.11)

операций, где 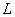 - размер импульсного отклика. Как показано в разд. 11.2, для получения свертки с применением быстрого преобразования Фурье необходимо примерно

                     (11.6.12)

операций. Степень относительной эффективности трех типов обработки зависит от размеров массива импульсного отклика [27]. Если эти размеры невелики, то для прямого метода получения свертки и рекурсивной фильтрации требуется почти одинаковое число арифметических операций. В этом случае сравнить эффективность обоих методов с эффективностью получения свертки с использованием БПФ можно с помощью графика на рис. 11.3.2. При больших размерах массива импульсного отклика быстрый метод получения свертки оказался гораздо эффективнее прямого метода. Сравнивая число операций в равенствах (11.6.10) и (11.6.12), можно показать, что при больших размерах импульсного отклика рекурсивная фильтрация оказывается эффективнее быстрого метода получения свертки, если площади массивов коэффициентов рекурсивного фильтра удовлетворяют неравенству

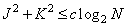,               (11.6.13)

где  - постоянная, принимающая значения от 1 до 20, причем ее величина зависит от вида использованного алгоритма БПФ и от того, насколько вычисления с комплексными числами происходят медленнее, чем с действительными.

Выводы из данной статьи про рекурсивная фильтрация указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое рекурсивная фильтрация и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений