10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ

Привет, Вы узнаете о том , что такое алгоритмы вычислений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритмы вычислений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

В общем случае, чтобы выполнить унитарное преобразование матрицы изображения, содержащей 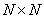 элементов, и получить матрицу из  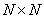спектральных коэффициентов, необходимо произвести примерно  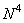арифметических операций (умножений и сложений). Если размеры матрицы изображения велики, то число операций становится чрезмерно большим. К счастью, для многих унитарных преобразований существуют эффективные алгоритмы вычислений , позволяющие ускорить выполнение преобразования.

Основной идеей этих быстрых вычислительных алгоритмов является разделение всей задачи на ряд этапов, причем результаты, полученные на предыдущих этапах, многократно используются на последующих этапах. В качестве примера рассмотрим процесс вычисления коэффициентов преобразования Адамара с неупорядоченной матрицей для последовательности из четырех элементов 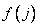. При прямом способе вычисления находятся четыре величины по формулам

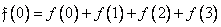,              (10.10.1а)

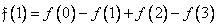,               (10.10.1б)

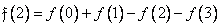,              (10.10.1в)

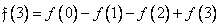.               (10.10.1г)

Для этого необходимо выполнить 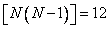 арифметических операций (сложений и вычитаний). Однако коэффициенты преобразования Адамара можно найти по-другому, разбив, процесс вычисления на следующие этапы:

Первый этап

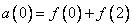,             (10.10.2а)

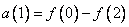,              (10.10.2б)

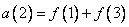,              (10.10.2в)

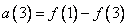.              (10.10.2г)

Второй этап

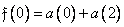,               (10.10.3а)

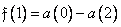,                (10.10.3б)

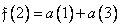,                (10.10.4в)

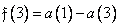.                (10.10.3г)

При этом для определения элементов матрицы 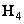 требуется только  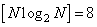операций, т. Об этом говорит сайт https://intellect.icu . е. экономится четыре операции.

Ход вышеуказанных вычислений можно описать с помощью графа (рис. 10.10.1). Общее число операций равно половине числа ребер, соединяющих вершины графа. Другой способ представления того же процесса заключается в факторизации матрицы, когда матрицу преобразования Адамара 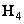 записывают в виде произведения двух разреженных матриц. Так, например,

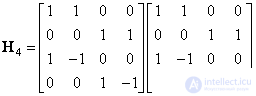.                 (10.10.4)

Число операций равно половине числа ненулевых элементов в обеих матрицах-сомножителях.

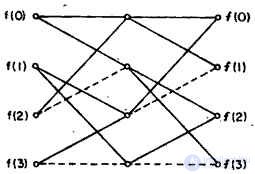
Рис. 10.10.1. Граф вычисления коэффициентов преобразовании Адамара для четырехэлементной последовательности. (Сплошные линии обозначают операции сложения, пунктирные - вычитания.)

Принципы, описанные выше на примере преобразования Адамара, можно применить для быстрого вычисления многих других преобразований. Разработаны быстрые алгоритмы для преобразований Фурье [35], четного косинусного [12], синусного [13], Адамара [17], Хаара [1] и наклонного [26]. В общем случае для преобразования Карунена-Лоэва быстрого алгоритма не найдено, однако известны приближенные алгоритмы преобразования Карунена-Лоэва для марковских процессов.

Для большинства одномерных унитарных преобразований порядок требуемого числа арифметических операций равен 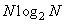. Исключением является преобразование Хаара, которое имеет разреженную матрицу и поэтому может быть вычислено с помощью примерно  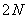операций. Для унитарных преобразований пока неизвестен общий метод построения эффективных вычислительных алгоритмов [36]. В каждом случае приходится отыскивать эффективную процедуру вычислений или способ представления матрицы в виде произведения разреженных матриц.

Унитарные преобразования, основанные на базисных векторах синусоидального характера (преобразования Фурье, косинусное, синусное), можно выполнить косвенным путем, пользуясь алгоритмом так называемого 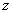-преобразования с ЛЧМ-фильтрацией. Преобразование Фурье одномерной последовательности  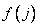определяется соотношением

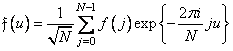.                       (10.10.5).

Произведя замену переменных

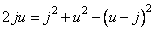,                   (10.10.6)

можно получить выражение

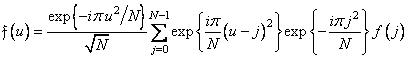.               (10.10.7)

Формула (10.10.7) описывает совокупность следующих операций:

1. Поэлементное умножение последовательности 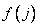 на множители с квадратично изменяющейся фазой .

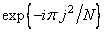2. Свертка результатов предыдущей операции с ядром .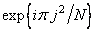

3. Поэлементное умножение полученной последовательности на множители с квадратичной фазой .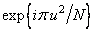

На рис. 10.10.2 приведена структурная схема алгоритма вычисления коэффициентов преобразования Фурье с использованием метода 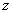-преобразования с ЛЧМ-фильтрацией. Если обработка производится в универсальной ЦВМ, то, как правило, применять этот алгоритм не следует, поскольку для вычисления свертки требуется большее число операций, чем для прямого выполнения преобразования методом БПФ. Однако с помощью аналоговых трансверсальных фильтров очень легко осуществить 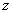-преобразование с ЛЧМ-фильтрацией, что дает возможность вычисления коэффициентов преобразования Фурье, а также косинусного и синусного преобразований поточным способом.

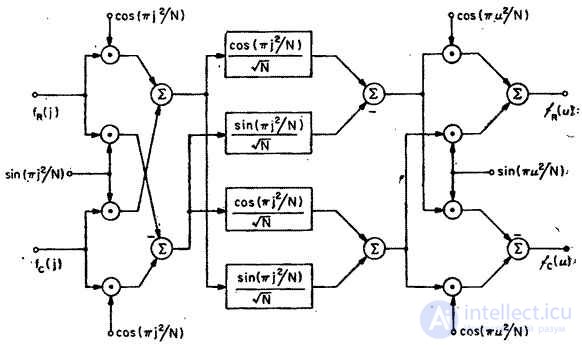
Рис. 10.10.2. Блок-схема алгоритма преобразования Фурье с использованием метода 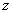-преобразования.

Выводы из данной статьи про алгоритмы вычислений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритмы вычислений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений