Лекция
Привет, сегодня поговорим про обобщенные линейные системы, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое обобщенные линейные системы , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
В разделе 1.4 были введены понятия линейности и суперпозиции с тем, чтобы распространить понятие линейности на более широкий класс систем.
Рассмотрим две функции, описывающие изображения,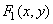 
и 
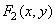, которые, взаимодействуя некоторым образом 
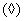, дают функцию 
:
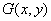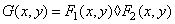. (1.8.1)
Пусть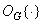 
- оператор системы, преобразующей 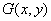, который обладает следующими свойствами:
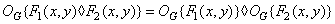(1.8.2a)
и
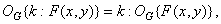(1.8.2б)
где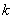 
- постоянная, а двоеточие обозначает обобщенное умножение на постоянную. Об этом говорит сайт https://intellect.icu . В работе [4] показано, что если операция 
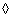сводится к сложению векторов, а операция : - к умножению вектора на скаляр, то оператор 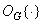может быть представлен в виде цепочки операторов, называемой гомоморфным фильтром (рис. 1.8.1). Первый оператор 
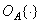превращает операции 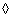и : в сложение векторов и умножение вектора на скаляр:
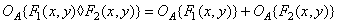(1.8.3а)
и
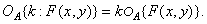(1.8.3б)
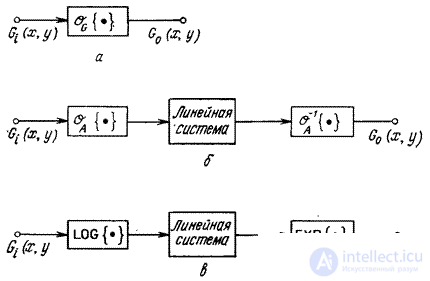
Рис. 1.8.1. обобщенные линейные системы : а — обобщенная система; б — представление обобщенной системы в виде гомоморфного фильтра; в - мультипликативный гомоморфный фильтр.
Вторая ступень гомоморфного фильтра – обычная линейная система. Третья ступень – оператор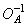 
, который является обратным относительно первого оператора, т.е.
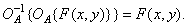(1.8.4)
Рис. 1.8.1, в иллюстрирует частный случай гомоморфного фильтра для мультипликативной системы [5], в которой функция 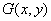получается в результате перемножения функци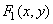й и 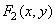, т.е.
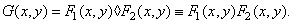(1.8.5)
Прологарифмировав обе части равенства (1.8.5), получим сумму логарифмов функци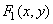й и :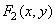
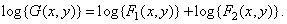(1.8.6)
Функция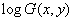 
преобразуется некоторой линейной системой, а затем посредством экспоненциального преобразования возвращается в пространство исходных изображений. Операция обобщенного умножения вектора на скаляр определяется как возведение в степень
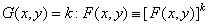(1.8.7)
Логарифмирование этого равенства дает
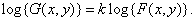(1.8.8)
Применение гомоморфной фильтрации при восстановлении изображений рассмотрено в гл. 15.
Надеюсь, эта статья про обобщенные линейные системы, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое обобщенные линейные системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про обобщенные линейные системы
Комментарии