11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ кратко

Привет, Вы узнаете о том , что такое суперпозиция с преобразованием, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое суперпозиция с преобразованием , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Операцию суперпозиции, описанную в гл. 9, часто удается выполнить более эффективно, если вместо непосредственной обработки проводить обработку с использованием преобразования. На рис. 11.2.1,а,б приведены схемы непосредственного выполнения конечной суперпозиции и дискретизованной суперпозиции. На рис. 11.2.1,г,д представлены схемы осуществления операции суперпозиции, когда вектор 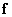подвергается унитарному преобразованию, результат которого умножается на матрицу (для оператора суперпозиции конечных массивов) или матрицу 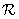(для дискретизованного оператора суперпозиции). Обратное преобразование дает обработанный вектор. Согласно рис. 11.2.1,а,г, в случае применения оператора суперпозиции конечных массивов исходный и обработанный векторы связаны следующими соотношениями:

(11.2.1а)

и

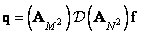. (11.2.1б)

Поэтому матрицу можно представить в виде произведения

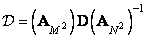. (11.2.2а)

Аналогично

. (11.2.2б)

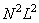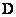Чтобы непосредственно выполнить суперпозицию конечных массивов, требуется примерно операций (здесь - порядок матрицы импульсного отклика). В этом случае коэффициент заполнения матрицы равен

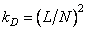. (11.2.3а)

Для суперпозиции дискретизованных массивов требуется около операций, а коэффициент заполнения матрицы равен

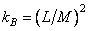. (11.2.3б)

На рис. 11.2.1,е приведена блок-схема циклической суперпозиции с преобразованием. В этом случае входным вектором 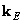служит так называемый расширенный входной вектор, получаемый размещением матрицы исходного изображения 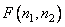в левом углу квадратной нулевой матрицы 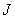-го порядка и разверткой полученной матрицы по столбцам. Повторяя вышеприведенные рассуждения, можно показать, что

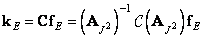(11.2.4a)

и, следовательно,

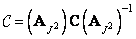. (11.2.4б)

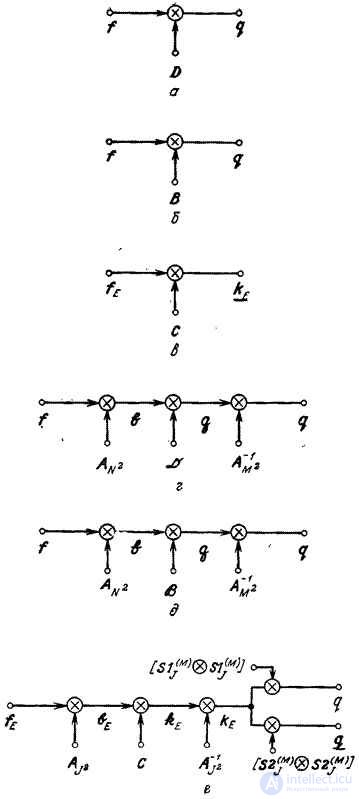
Рис. Об этом говорит сайт https://intellect.icu . 11.2.1. Различные виды суперпозиции.

а - конечная суперпозиция; б - дискретизованная интегральная суперпозиция; в - циклическая суперпозиция; г - конечная суперпозиция с преобразованием ; д - дискретизованная интегральная суперпозиция с преобразованием; е - циклическая суперпозиция с преобразованием.

Как было отмечено в гл. 9, для суперпозиции конечных или дискретизованных массивов эквивалентный выходной вектор можно сформировать из 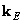, выбирая определенные компоненты последнего. Для суперпозиции конечных массивов

, (11.2.5а)

а для суперпозиции дискретизованных массивов

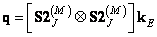. (11.2.5б)

При суперпозиции конечных массивов матрица обработанного изображения связана с расширенной матрицей изображения следующим образом:

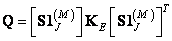. (11.2.6а)

При суперпозиции дискретизованных массивов матрица обработанного изображения равна

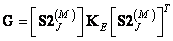. (11.2.6б)

Число арифметических операций, необходимых для вычисления вектора 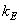путем обработки с преобразованием, можно найти из приведенных выше формул, если положить :

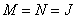Прямое преобразование: .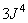

Быстрое преобразование: .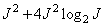

Если матрица 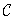разрежена, то многие из 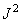умножений, нужных для операции фильтрации, выполняться не будут.

Из вышеизложенного нетрудно сделать вывод, что для эффективного проведения суперпозиции следует подобрать преобразование, отвечающее двум требованиям: во-первых, для него должен существовать быстрый алгоритм, а, во-вторых, матрица фильтрации преобразованных массивов должна быть разреженной. В качестве примера рассмотрим свертку конечных массивов, получаемую с помощью преобразования Фурье [2, 3]. В соответствии с рис. 11.2.1 положим

, (11.2.7)

где

при 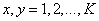. Кроме того, примем, что вектор 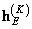размера 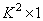представляет расширенную матрицу пространственно-инвариантного импульсного отклика, описываемого формулами (9.3.2) при 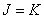. Преобразование Фурье от 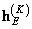обозначим через

. (11.2.8)

Полученные отсчеты преобразования расставим на главной диагонали матрицы размера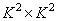

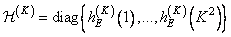. (11.2.9)

С помощью весьма громоздких выкладок можно показать, что в спектральном пространстве матрицы оператора свертки конечных массивов и дискретизованного оператора свертки можно представить в следующем виде :

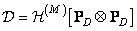(11.2.10)

пр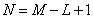и и

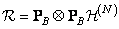(11.2.11)

при 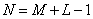, где

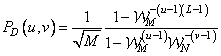, (11.2.12а)

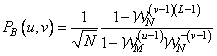. (11.2.12б)

Таким образом, оба оператора свертки в спектральном пространстве содержат матрицу скалярных весовых множителей 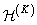и интерполяционную матрицу 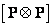, которая позволяет связать входной вектор размера 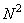с выходным вектором размера 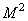. Как правило, интерполяционная матрица 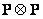содержит много нулевых элементов, и поэтому свертка с использованием преобразования выполняется весьма эффективно.

Рассмотрим теперь циклическую свертку, выполняемую с переходом в спектральное пространство. С помощью рассуждений, аналогичных вышеприведенным, было показано , что оператор фильтрации в этом случае сводится к скалярному оператору

. (11.2.13)

Таким образом, как видно из равенств (11.2.12) и (11.2.13), при свертке в пространстве спектров Фурье матрицу фильтра удается выразить в компактной замкнутой форме. Для других унитарных преобразований подобных выражений не найдено.

Эффективность вычисления свертки с применением преобразования Фурье определяется тем, что оператор свертки 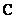имеет циклическую матрицу, а соответствующая матрица фильтра 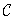является диагональной. Как можно увидеть из соотношений (11.1.6), базисные векторы преобразования Фурье фактически являются собственными векторами матрицы 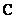. Это не так для операции суперпозиции общего вида, а также для операции свертки с применением других унитарных преобразований. Однако во многих случаях матрицы фильтра 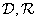и 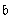содержат сравнительно мало ненулевых элементов и обработка с преобразованием позволяет уменьшить объем вычислений.

На рис. 11.2.2 показан вид матриц спектров для трех типов оператора свертки одномерного входного вектора с гауссовым импульсным откликом с использованием преобразований Фурье и Адамара . Как и ожидалось, матрицы коэффициентов преобразования оказались значительно более разреженными, чем исходные матрицы. Кроме того, легко заметить, что для циклической свертки с преобразованием Фурье матрица фильтра является диагональной. На рис. 11.2.3 показана структура матриц трех операторов свертки двумерных сигналов .

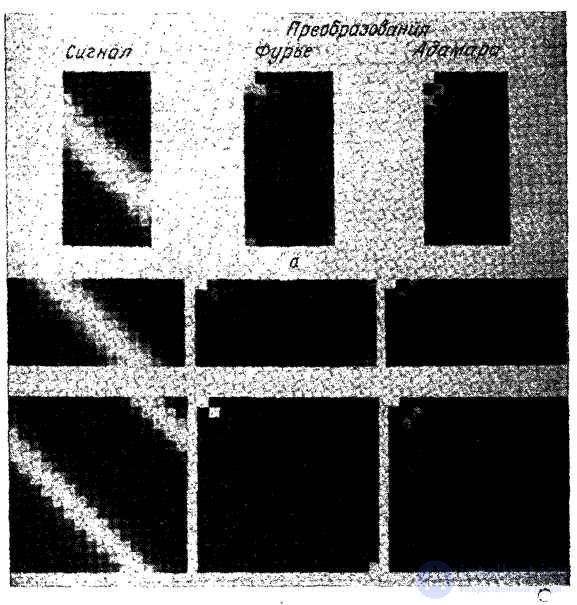
Рис. 11.2.2. Матрицы операторов свертки одномерных сигналов с использованием преобразований Фурье и Адамара.

а - конечная свертка; б - дискретизованная свертка; в - циклическая свертка.

Рис. 11.2.3. Матрицы операторов свертки двумерных сигналов с использованием преобразования Фурье.

Конечная свертка: а - непосредственно выполняемая; б - с преобразованием. Дискретизованная интегральная свертка: в - непосредственно выполняемая; г - с преобразованием.

Циклическая свертка: д - непосредственно выполняемая; е - с преобразованием.

Выводы из данной статьи про суперпозиция с преобразованием указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое суперпозиция с преобразованием и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про суперпозиция с преобразованием