Лекция
Привет, сегодня поговорим про дискретизация случайных изображений , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дискретизация случайных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
Выше при анализе вопросов о дискретизаций и восстановлении, изображений предполагалось, что функция 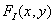 , описывающая исходное изображение, является детерминированной. Было показано, что если это изображение имеет спектр ограниченной ширины, то совокупность отсчетов изображения, взятых с найквистовской частотой в дискретных точках, достаточна, чтобы с помощью интерполяции восстановить из отсчетов точную копию исходного изображения. Подобный вывод справедлив и в случае дискретизации случайных двумерных полей. Пусть
, описывающая исходное изображение, является детерминированной. Было показано, что если это изображение имеет спектр ограниченной ширины, то совокупность отсчетов изображения, взятых с найквистовской частотой в дискретных точках, достаточна, чтобы с помощью интерполяции восстановить из отсчетов точную копию исходного изображения. Подобный вывод справедлив и в случае дискретизации случайных двумерных полей. Пусть 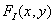 обозначает непрерывный двумерный стационарный случайный процесс с известными средним значением
обозначает непрерывный двумерный стационарный случайный процесс с известными средним значением 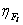 иавтокорреляционной функцией
иавтокорреляционной функцией
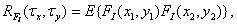 (4.1.17)
(4.1.17)
где 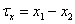 и
и 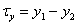 . С помощью набора дельта-функций произведем дискретизацию этого процесса. В результате получим
. С помощью набора дельта-функций произведем дискретизацию этого процесса. В результате получим
 (4.1.18)
(4.1.18)
Автокорреляционная функция дискретизованного процесса имеет вид
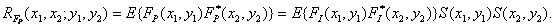 (4.1.19)
(4.1.19)
Первый сомножитель правой части этого равенства является автокорреляционной функцией стационарного исходного изображения. Следует учесть, что стоящее в правой части равенства (4.1.19) произведение двух дискретизирующих дельта-функций есть дельта-функция вида
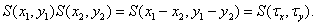 (4.1.20)
(4.1.20)
Следовательно, дискретизованное случайное поле, представляющее изображение, также стационарно и имеет автокорреляционную функцию
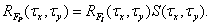 (4.1.21)
(4.1.21)
С помощью двумерного преобразования Фурье автокорреляционной функции (4.1.21) найдемэнергетический спектр дискретизованного случайного поля. Об этом говорит сайт https://intellect.icu . Согласно теореме о спектре произведения,
 (4.1.22)
(4.1.22)
где 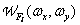 и
и 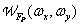 обозначают соответственно спектральные плотности исходного и дискретизованного изображений, а
обозначают соответственно спектральные плотности исходного и дискретизованного изображений, а 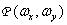 - результат преобразования Фурье дискретизирующих дельта-функций. Далее, повторяя шаги, сделанные при выводе соотношения (4.1.7), получим, что энергетический спектр дискретизованного изображения можно записать в следующем виде:
- результат преобразования Фурье дискретизирующих дельта-функций. Далее, повторяя шаги, сделанные при выводе соотношения (4.1.7), получим, что энергетический спектр дискретизованного изображения можно записать в следующем виде:
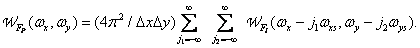 (4.1.23)
(4.1.23)
Таким образом, энергетический спектр дискретизованного изображения образуется повторениемэнергетического спектра непрерывного исходного изображения в пространственно-частотной области через интервалы, кратные пространственной частоте дискретизации 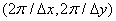 . Если ширина энергетического спектра непрерывного изображения ограничена так, что
. Если ширина энергетического спектра непрерывного изображения ограничена так, что 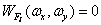 при
при 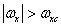 и
и 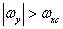 где
где 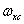 и
и 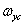 - граничные частоты, то в сумме (4.1.23) отдельные спектры не будут накладываться в том случае, когда интервалы дискретизации удовлетворяют условиям
- граничные частоты, то в сумме (4.1.23) отдельные спектры не будут накладываться в том случае, когда интервалы дискретизации удовлетворяют условиям 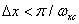 и
и 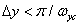 . Непрерывное случайное изображение
. Непрерывное случайное изображение 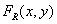 можно восстановить из отсчетов исходного случайного изображения с помощью интерполяции по формуле
можно восстановить из отсчетов исходного случайного изображения с помощью интерполяции по формуле
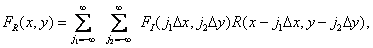 (4.1.24)
(4.1.24)
где 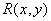 - детерминированная интерполяционная функция. Можно добиться, чтобы восстановленное поле и исходное изображение были эквивалентны в среднеквадратическом смысле [5, стр. 284], т. е.
- детерминированная интерполяционная функция. Можно добиться, чтобы восстановленное поле и исходное изображение были эквивалентны в среднеквадратическом смысле [5, стр. 284], т. е.
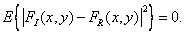 (4.1.25)
(4.1.25)
Для этого достаточно, чтобы удовлетворялся критерий Найквиста и в качестве интерполяционной функции была выбрана достаточно «хорошая» функция, как, например, бесселева или функция 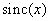 , определяемые формулами (4.1.16) и (4.1.14).
, определяемые формулами (4.1.16) и (4.1.14).
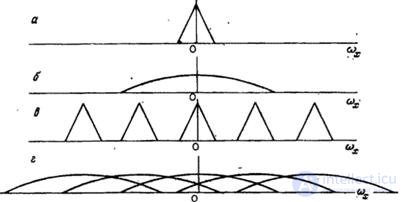
Рис. 4.1.4. Спектры дискретизованного изображения, содержащего сигнал и помеху.
а - сигнал: б - помеха; в - дискретизованный сигнал; г - дискретизованная помеха.
Приведенные результаты можно непосредственно применить к практической задаче о дискретизации суммы детерминированного изображения и аддитивного шума, моделью которого служит случайное поле. На рис. 4.1.4 показан пример энергетического спектра дискретизованного зашумленного изображения. Этот пример указывает на возможность возникновения серьезной трудности. Спектр шума может оказаться шире спектра полезного изображения, и если шум будет дискретизироваться с недостаточной частотой, то в полосу пропускания восстанавливающего фильтра будут попадать «хвосты» шумового спектра. Это приведет к увеличению искажений, вызванных шумом. Для устранения этой трудности перед дискретизацией следует, конечно, профильтровать зашумленное изображение с тем, чтобы сузить спектр шума.
Надеюсь, эта статья об увлекательном мире дискретизация случайных изображений , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое дискретизация случайных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про дискретизация случайных изображений
Комментарии
Оставить комментарий
Цифровая обработка изображений
Термины: Цифровая обработка изображений