8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ кратко

Привет, Вы узнаете о том , что такое операторы псевдообращения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое операторы псевдообращения , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

В контексте цифровой обработки изображений и сигналов операторы псевдообращения относятся к операторам, которые используются для выполнения различных операций обработки изображений.

При линейной обработке сигналов часто встречается задача «обращения» преобразования вида

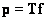(8.3.1)

с тем, чтобы выразить точное значение входного вектора 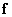размера 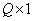или некоторую его оценку 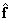через выходной вектор p размера 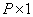. Если 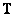- квадратная матрица, то очевидно, что

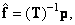(8.3.2)

если обратная матрица существует. Если матрица 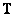не квадратная, то для отыскания решения можно воспользоваться псевдообратной матрицей 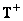размера 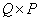. В этом случае

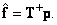(8.3.3)

Если решение существует и единственно, то «правильным» оператором псевдообращения будет тот, который обеспечивает точную оценку, т. е. 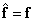. Это означает, что вектор 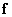можно определить по наблюдаемому вектору 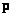без ошибок. Если решение существует, но оно не единственно, то с помощью псевдообратного оператора можно выбрать решение с минимальной нормой. Если, наконец, точных решений не существует, то с помощью оператора псевдообращения можно найти наилучшее приближенное решение. Более подробно этот вопрос рассмотрен в последующих разделах. Разъяснения и доказательства многих из нижеприведенных положений содержатся в монографиях [4-6].

Первым из операторов псевдообращения будет рассмотрен оператор с обобщенной обратной матрицей 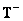, для которой выполняются следующие соотношения:

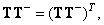(8.3.4а)

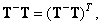(8.3.46)

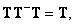(8.3.4в)

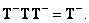(8.3.4г)

Обобщенная обратная матрица является единственной и при некоторых условиях ее можно записать в явном виде. Об этом говорит сайт https://intellect.icu . Если 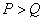, то систему уравнений (8.3.1) называют переопределенной, т. е. число компонент наблюдаемого вектора 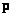превышает число подлежащих оценке компонент вектора 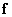. Если при этом ранг матрицы 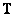равен 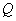, то обобщенная обратная матрица

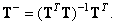(8.3.5)

В противоположном случае, когда 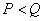, систему (8.3.1) называют недоопределенной. Если при этом ранг матрицы 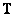равен 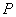, то обобщенная обратная матрица имеет вид

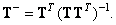(8.3.6)

Нетрудно показать, что матрицы, определенные соотношениями (8.3.5) и (8.3.6), удовлетворяют условиям (8.3.4). Если матрица 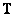может быть представлена в виде прямого произведения (8.1.8), то обобщенная обратная матрица имеет вид

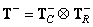(8.3.7)

где 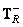и 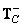- обобщенные обратные матрицы для линейных операторов обработки строк и столбцов. В этом случае сокращается объем вычислений, необходимых для обращения.

Еще один тип оператора псевдообращения имеет матрицу 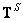, называемую матрицей обращения методом наименьших квадратов, которая определяется следующими соотношениями:

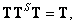(8.3.8а)

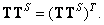(8.3.8б)

И наконец, условно обратная матрица 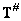определяется формулой

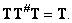(8.3.9)

Анализ определений всех трех видов оператора псевдообращения показывает, что обобщенный обратный оператор является оператором обращения методом наименьших квадратов, а последний - оператором условного обращения. Для любого линейного оператора с матрицей 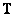всегда существуют матрица обращения методом наименьших квадратов и условно обратная матрица, но они могут быть не единственными. Кроме того, для этих матриц обычно не удается найти явное выражение в конечной форме.

Ниже приведены некоторые полезные соотношения для матрицы 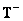, которая является обобщенной обратной матрицей относительно матрицы 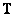размера .

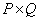Обобщенное обращение транспонированной матрицы

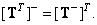(8.3.10)

Обобщенное обращение обобщенной обратной матрицы

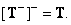(8.3.11)

Сохранение ранга

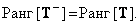(8.3.12)

Обобщенное обращение произведения матриц

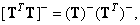(8.3.13)

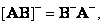(8.3.14)

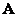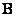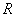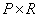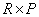где и — матрицы ранга , имеющие размеры и соответственно.

Обобщенное обращение произведения ортогональных матриц

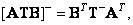(8.3.15)

где 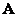и 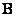- ортогональные матрицы размера 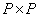и 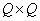соответственно.

Выводы из данной статьи про операторы псевдообращения указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое операторы псевдообращения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про операторы псевдообращения