10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ кратко

Привет, Вы узнаете о том , что такое косинусные преобразования, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое косинусные преобразования , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Известно, что ряд Фурье для любой непрерывной действительной и симметричной (четной) функции содержит только действительные коэффициенты, соответствующие косинусным членам ряда. В соответствующей интерпретации этот результат можно распространить и на дискретное преобразование Фурье изображений. Существуют [11] два способа получения симметричных изображений (рис. 10.3.1). Согласно первому из них, к изображению вплотную пристраивают его зеркальные отражения. По второму методу оригинал и отражения пристраивают, налагая крайние элементы. Таким образом, из первоначального массива, содержащего 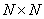элементов, в первом случае (называемом четным косинусным преобразованием) получается массив из 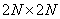элементов, а во втором случае (называемом нечетным косинусным преобразованием) - массив из 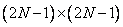элементов.

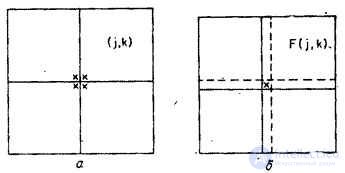
Рис. 10.3.1. Построение симметричного изображения, предназначенного для косинусного преобразования.

а - отражение относительно края: б - отражение относительно крайних элементов.

Четное симметричное косинусное преобразование

Допустим, что симметричный массив образован путем зеркального отражения исходного массива относительно его краев согласно соотношению

(10.3.1)

Построенный таким образом массив 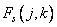симметричен относительно точки 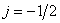, 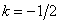. Вычислив преобразование Фурье для случая, когда начало координат находится в центре симметрии, получим

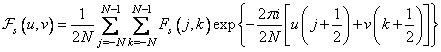, (10.3.2)

где 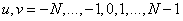. Поскольку массив 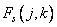симметричен и состоит из действительных чисел, соотношение (10.3.2) можно свести к виду

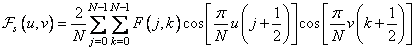. (10.3.3)

С другой стороны, спектральные составляющие вида (10.3.3) можно найти, вычисляя преобразование Фурье массива 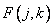по 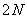точкам:

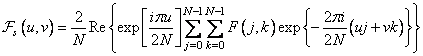. Об этом говорит сайт https://intellect.icu . (10.3.4)

Прямое четное косинусное преобразование по определению [12] равно сумме (10.3.3), умноженной на нормирующий множитель, т. е.

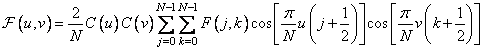, (10.3.5a)

а обратное преобразование определяется соотношением

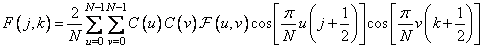, (10.3.5б)

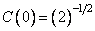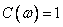где , а при 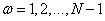. Оказалось, что базисные функции четного косинусного преобразования принадлежат к классу дискретных полиномов Чебышева [12].

На рис. 10.3.2 приведены графики базисных функций четного симметричного косинусного преобразования при 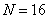. Образцы спектра, получаемого при четном симметричном косинусном преобразовании, приведены на рис. 10.3.3. Начало координат расположено в верхнем левом углу каждого снимка, что согласуется с принятым в теории матриц порядком. Следует отметить, что здесь, как и в случае преобразования Фурье, основная часть энергии изображения концентрируется в области низких пространственных частот.

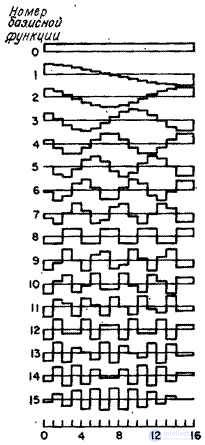
Рис. 10.3.2. Базисные функции косинусного преобразования.

Рис. 10.3.3. Косинусное преобразование изображения «Портрет».

а - исходное изображение: б - косинусный спектр в логарифмическом масштабе по оси амплитуд; в - спектр с ограниченными наибольшими гармониками.

Нечетное симметричное косинусное преобразование

При нечетном косинусном преобразовании строение симметричного массива определяется следующим образом:

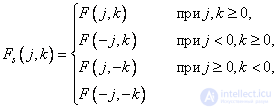(10.3.6)

Вычисление двумерного преобразования Фурье от такого массива дает

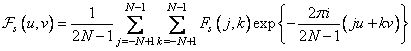, (10.3.7)

где 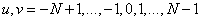. Поскольку преобразование Фурье обладает свойством симметрии относительно комплексного сопряжения, то для реальных изображений

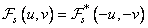. (10.3.8)

Следовательно, 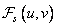достаточно вычислять только при неотрицательных значениях индексов 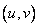. Кроме того, поскольку функция 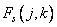принимает действительные значения и симметрична, то 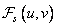также имеет действительные значения. Таким образом, соотношение (10.3.2) можно представить в следующем виде:

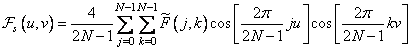, (10.3.9)

где массив 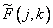получается из матрицы изображения 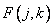взвешиванием ее элементов в соответствии с формулой

(10.3.10)

Нечетное косинусное преобразование есть просто нормированный вариант равенства (10.3.9), причем нормирование проведено так, чтобы базисные функции стали ортонормальными. Таким образом, нечетное косинусное преобразование определяется соотношениями

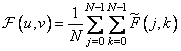при 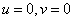, (10.3.11а)

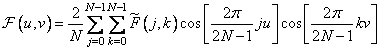при 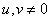. (10.3.11б)

Такое же преобразование

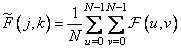при 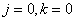, (10.3.12а)

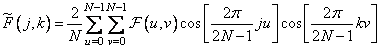при 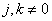(10.3.12б)

дает матрицу взвешенных отсчетов 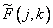. Тогда исходный массив можно восстановить с помощью формулы

(10.3.13)

Базисные функции нечетного косинусного преобразования являются разделимыми, так что двумерное нечетное косинусное преобразование можно выполнить с помощью последовательных одномерных преобразований. Кроме того, нечетное косинусное преобразование можно найти с помощью алгоритма преобразования Фурье при нечетном числе элементов, поскольку

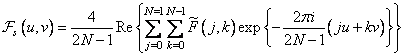. (10.3.14)

Пример дискретного косинусного преобразования.
Основное изображение (уровень серого) DCT основного изображения (косинусный спектр) .Логарифмическое масштабирование косинусного спектра

Вау!! 😲 Ты еще не читал? Это зря!

• Двумерные унитарные преобразования
• Операторы унитарных преобразований
• Синусное преобразование
• Преобразование Хаара
• Преобразование Карунена-Лоэва
• Функция Уолша

Выводы из данной статьи про косинусные преобразования указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое косинусные преобразования и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про косинусные преобразования