10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА

Привет, Вы узнаете о том , что такое преобразование карунена-лоэва, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое преобразование карунена-лоэва , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Метод преобразования непрерывных сигналов в набор некоррелированных коэффициентов разработан Каруненом [27] и Лоэвом [28]. Как указывается в статье [30], Хотеллинг [29] первым предложил метод преобразования дискретных сигналов в набор некоррелированных коэффициентов. Однако в большинстве работ по цифровой обработке сигналов и дискретное, и непрерывное преобразования называют преобразованием Карунена-Лоэва или разложением по собственным векторам.

В общем случае преобразование карунена-лоэва описывается соотношением

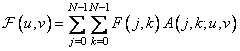,                     (10.8.1)

ядро 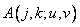 которого удовлетворяет уравнению

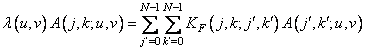,              (10.8.2)

где 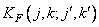 - ковариационная функция дискретизованного изображения, а  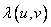при фиксированных  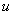и 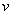 постоянна. Функции  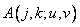являются собственными функциями ковариационной функции, а  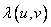- ее собственные значения. Как правило, выразить собственные функции в явной форме не удается.

Если ковариационную функцию можно разделить, т. е.

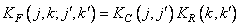,                     (10.8.3)

то ядро разложения Карунена-Лоэва также разделимо и

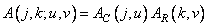.                  (10.8.4)

Строки и столбцы матриц, описывающих эти ядра, удовлетворяют следующим уравнениям:

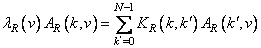,                (10.8.5)

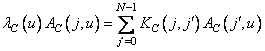.               (10.8.6)

В частном случае, когда ковариационная матрица описывает разделимый марковский процесс первого порядка, собственные функции удается записать в явной форме. Об этом говорит сайт https://intellect.icu . Для одномерного марковского процесса с коэффициентом корреляции 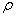 собственные функции и собственные значения имеют вид [3]

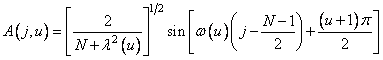                      (10.8.7)

и

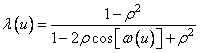,                    (10.8.8)

где 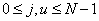, a 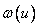 - корни трансцендентного уравнения

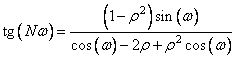.                      (10.8.9)

Собственные векторы можно также найти из рекуррентных формул [32]

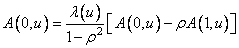,                      (10.8.10а)

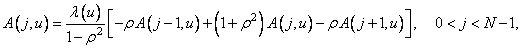                       (10.8.10б)

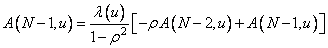,                       (10.8.10в)

положив в качестве начального условия 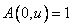 и затем пронормировав полученные собственные векторы.

Если исходное и преобразованное изображения представить в векторной форме, то пара преобразований Карунена-Лоэва будет иметь вид

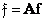            (10.8.11)

и

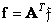.                     (10.8.12)

Матрица преобразования 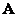 удовлетворяет уравнению

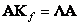,              (10.8.13)

где 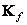 - ковариационная матрица вектора 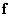;  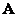- матрица, строки которой являются собственными векторами матрицы 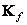;  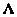- диагональная матрица вида

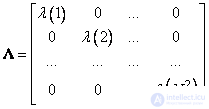.                 (10.8.14)

Если матрица 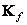 разделима, то

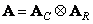,                       (10.8.15)

причем матрицы 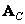 и 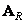 удовлетворяют следующим условиям:

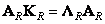,                    (10.8.16а)

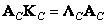,                   (10.8.16б)

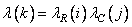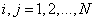а  при  [33].

На рис. 10.8.1 приведены графики базисных функций преобразования Карунена-Лоэва одномерного марковского процесса, для которого коэффициенты корреляции соседних элементов .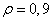

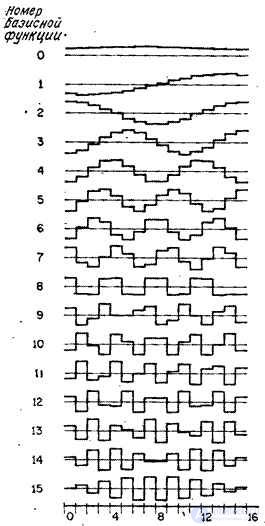
Pиc. 10.8.1. Базисные функции преобразования Карунена-Лоэва при .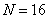

Выводы из данной статьи про преобразование карунена-лоэва указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое преобразование карунена-лоэва и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений