5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ

Привет, сегодня поговорим про статистическое описание дискретных изображений , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое статистическое описание дискретных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Статистические методы описания непрерывных изображений, приведенные в гл. 1, можно непосредственно применить и для описания дискретных изображений. В данном разделе получены выражения для моментов дискретных изображений. Модели совместных плотностей вероятностей приведены в следующем разделе.

 

Среднее значение матрицы, описывающей дискретное изображение, представляет собой матрицу

.                      (5.4.1)

Если эта матрица разверткой по столбцам преобразована в вектор, то среднее значение этого вектора есть

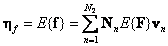.                (5.4.2)

Корреляция двух элементов изображения с координатам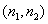и  и 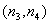 определяется как

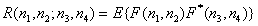.     (5.4.3)

Ковариация двух элементов изображения есть

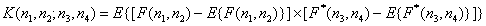.       (5.4.4)

И наконец, дисперсия элемента изображения равна

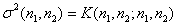.              (5.4.5)

Если матрица изображения преобразована в вектор 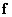, то корреляционную матрицу этого вектора можно выразить через корреляции элементов матрицы :

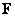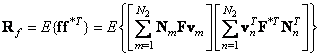,     (5.4.6a)

или

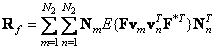.               (5.4.6б)

Выражение

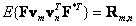                         (5.4.7)

представляет собой корреляционную матрицу 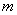-го и 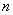-го столбцов матрицы  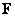и имеет размеры 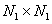. Об этом говорит сайт https://intellect.icu . Следовательно,  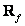можно представить в виде блочной матрицы

     (5.4.8)

Ковариационную матрицу вектора 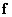 можно получить на основе его корреляционной матрицы и вектора средних значений с помощью соотношения

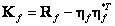.                              (5.4.9)

Матрица дисперсий 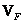 массива чисел  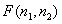по определению является матрицей, элементы которой равны дисперсиям соответствующих элементов массива. Элементы матрицы  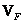можно непосредственно выделить из блоков матрицы :

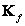.                             (5.4.10)

Если дискретное изображение представляется массивом, стационарным в широком смысле, то его корреляционную функцию можно записать в виде

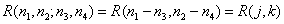,          (5.4.11)

где 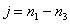 и 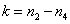. Соответственно блоки ковариационной матрицы (5.4.9) будут связаны соотношениями

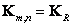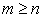,     ,                 (5.4.12а)

,     ,     (5.4.12б)

где 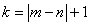. Таким образом, для стационарного в широком смысле массива

  (5.4.13)

Матрица (5.4.13) является блочно-теплицевой [11]. Наконец, если корреляционную функцию изображения можно записать в виде произведения корреляционных функций строк и столбцов, то ковариационную матрицу вектора 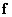, представляющего изображение, можно записать в виде прямого произведения ковариационных матриц для строк и столбцов:

      (5.4.14)

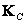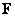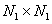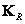где  - ковариационная матрица столбцов матрицы , имеющая размеры , а  - ковариационная матрица строк матрицы  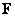с размерами .

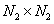Рассмотрим случай, когда ковариационная матрица строк матрицы 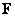 имеет следующий вид:

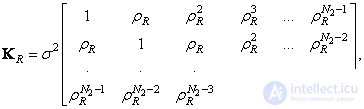   (5.4.15)

где  - дисперсия элементов изображения. Эта ковариационная матрица - аналог непрерывной автоковариационной функции вида 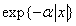 - описывает марковский процесс. На рис. 5.4.1 приведены полученные Дэвиссоном [12] значения коэффициентов корреляции элементов строки типичного изображения. Экспериментальные точки хорошо аппроксимируются ковариационной функцией марковского процесса с параметром 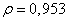. Аналогично значения коэффициентов корреляции в направлении, перпендикулярном к строкам, хорошо согласуются с марковской ковариационной функцией при 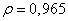. Если ковариационная функция может быть представлена в виде (5.4.14), то коэффициенты корреляции по диагонали должны быть равны произведению соответствующих коэффициентов корреляции вдоль строк изображения и в направлении, перпендикулярном к ним. В данном примере оказалось, что такая аппроксимация является достаточно точной в области от нуля до пяти шагов дискретизации.

По аналогии с непрерывным энергетическим спектром (1.8.11) можно определить дискретную спектральную плотность дискретного стационарного двумерного случайного поля, представляющего изображение, как результат двумерного дискретного преобразования Фурье автокорреляционной функции этого поля. Тогда в силу равенства (5.4.11) будем иметь

     (5.4.16)

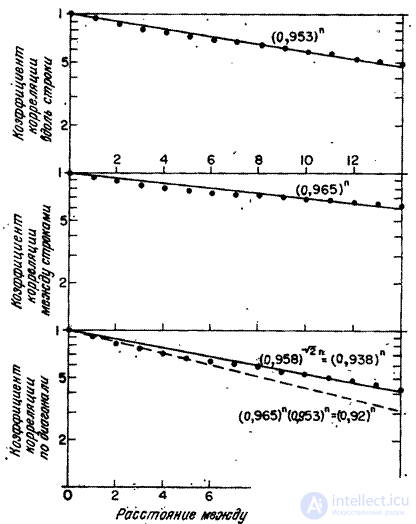
Рис. 5.4.1. Пример корреляционных зависимостей между соседними элементами изображения.

На рис. 5.4.2 приведены энергетические спектры марковских процессов.

Надеюсь, эта статья об увлекательном мире статистическое описание дискретных изображений , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое статистическое описание дискретных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про статистическое описание дискретных изображений