7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ

Привет, Вы узнаете о том , что такое дешифрируемость изображений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое дешифрируемость изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Определение количественной меры дешифрируемости изображения, т. е. степени его пригодности для анализа наблюдателем, является гораздо более сложной задачей, чем измерение верности воспроизведения изображений. Факторы, влияющие на дешифрируемость, глубоко связаны со свойствами человеческого зрения. Способность человека-наблюдателя извлекать из изображений информацию зависит, очевидно, от физических свойств зрительной системы, которые определяются, в частности, оптическими свойствами глаза, нелинейной реакцией фоторецепторов на яркость и наличием латерального торможения. Однако алгоритмы обработки данных, поступающих от глаза в мозг, играют важную и, по-видимому, решающую роль в процессе извлечения человеком визуальной информации из изображения. Поскольку механизмы зрительного восприятия пока изучены слабо, то в настоящее время попытки создать критерий дешифрируемости изображений, основанный на модели зрительной системы человека, представляются безнадежными. Следует скорее остановиться на каких-то частных критериях, которые достаточно хорошо согласовывались бы с результатами субъективных оценок.

В большинстве экспериментов по экспертной оценке дешифрируемости изображений используются простые штриховые фигуры, как, например, оптометрические таблицы, составленные из подобранных случайным образом букв разного размера. На рис. 7.8.1 представлены четыре контрольные таблицы, применявшиеся в экспериментах по распознаванию объектов [51]. Таблицы Лан-дольта [52, 53] составлены из строк буквы C, которая может находиться в любом из четырех (или восьми) возможных положений, причем размеры букв от строки к строке уменьшаются. Об этом говорит сайт https://intellect.icu . Цифровая таблица составлена из «криволинейных» цифр 3, 5, 6, 8 и 9, ориентированных случайным образом. В таблице из звездочек в каждом символе отсутствует какой-то один из шести лучей. Наблюдатель должен распознать символы во всех таблицах; результаты эксперимента выражаются в виде зависимости вероятности правильного ответа от размера символа. Подобные эксперименты на дискретизованных вариантах четырех таблиц, показанных на рис. 7.8.1, проводил Бернард [51]. Результаты приведены на рис. 7.8.2. В этих экспериментах были дискретизованы изображения на диапозитивах, затем к отсчетам прибавляли гауссов шум и результаты записывались на фотопленке в виде диапозитива. Как и ожидалось, с уменьшением размеров символов вероятность распознавания монотонно убывает. Бернард заметил также, что в экспериментах с цифрами наблюдается больший разброс, чем в опытах со звездочками или с таблицами Ландольта. Кроме того, оказалось, что вероятность правильного различения цифр зависит от их ориентации.

Так, при распознавании повернутой цифры «3» ошибки делали чаще, чем при распознавании такой же цифры, стоящей в нормальном положении. Можно предполагать, что в экспериментах со звездочками и таблицами Ландольда такой зависимости не наблюдалось потому, что у этих символов нет «стандартной» ориентации. Бернард [51] для предсказания результатов эксперимента по различению человеком символов в таблицах Ландольта применял теорию согласованной фильтрации. Вероятность правильного распознавания 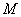 ортогональных сигналов ( 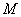ориентаций символа) в присутствии аддитивного гауссова шума аппроксимировалась [54] выражением

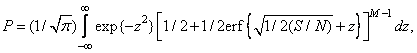     (7.8.1)

где  — отношение мощностей сигнала и шума. Как показано на рис. 7.8.2, б, в, теоретические и экспериментальные результаты согласуются довольно хорошо.

Рис. 7.8.1. Испытательные таблицы для экспериментов по распознаванию символов [51]: а – кольца Ландольга; б – кольца Ландольга с восемью позициями; в – цифры; г – звездочки.

Рис. 7.8.2. Результаты экспериментов по распознаванию символов [51]: а – таблица цифр; б – таблица с кольцами Ландольга (четыре позиции); в – таблица с кольцами Ландольга (восемь позиций); г – таблица звездочек.

Был проведен ряд опытов по оценке разборчивости цифро-буквенных символов, переданных с помощью фототелеграфных аппаратов. Арпс и др. [55] обнаружили, что для достижения 97,5 %-ной вероятности правильного распознавания необходимо, чтобы разрешение при дискретизации символа было порядка одной десятой наибольшего размера символа. Эрдман и Нил [56] изучали, как изменяется разборчивость слов в зависимости от разборчивости букв, связности текста и других семантических факторов.

Проводились также исследования с целью определения «рабочих характеристик» человека при визуальном анализе многоградационных изображений [57]. Однако исследования в этом направлении все еще находятся на начальной стадии своего развития.

Выводы из данной статьи про дешифрируемость изображений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое дешифрируемость изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений