Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ кратко

Привет, сегодня поговорим про математическое описание дискретных изображений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое математическое описание дискретных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

В гл. 2 были рассмотрены вопросы, связанные с математическим описанием непрерывных изображений. В настоящей главе даны способы формального представления дискретных изображений с использованием как детерминированных, так и статистических моделей.

5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ

В данном разделе коротко рассмотрены встречающиеся в тексте математические действия, выполняемые с векторами и матрицами. Строгий вывод и доказательства теорем и положений, приведенных ниже, можно найти в литературе [1-5].

Вектор

Вектор-столбец размера представляет собой совокупность элементов 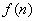, где , расположенных в виде вертикального столбца

(5.1.1)

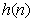Вектор-строка размера представляет собой упорядоченную совокупность элементов , где 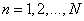, расположенных в виде горизонтальной строки

(5.1.2)

В книге полужирными строчными буквами будут, как правило, обозначаться вектор-столбцы. Вектор-строка будет обозначаться как транспонированный вектор-столбец:

(5.1.3)

Матрица

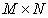Матрица размера представляет собой совокупность элементов где и , расположенных в виде строк и столбцов двумерной таблицы

(5.1.4)

Символ обозначает нулевую матрицу, все элементы которой равны нулю. Диагональная матрица – это квадратная матрица (когда ), все элементы которой, не лежащие на главной диагонали, равны нулю, т.е. , если 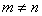. Единичная матрица, обозначаемая символом 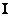, есть диагональная матрица, все диагональные элементы которой равны единице. Индекс при символе единичной матрицы указывает ее размеры; обозначает единичную матрицу размера . Матрица может быть разделена на блоки (подматрицы) :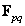

. (5.1.5)

Сложение матриц

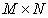Сумма двух матриц определена только в том случае, когда обе матрицы имеют одинаковые размеры. Матрица - сумма матриц и , имеет размеры , а ее элементы .

Умножение матриц

Произведение двух матриц определено только тогда, когда число столбцов матрицы равно числу строк матрицы . При умножении матрицы размера на матрицу размера получается матрица размера 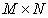, элементы которой определяются равенством

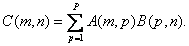(5.1.6)

При умножении матрицы на скаляр 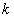получается матрица , элементы которой .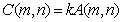

Обращение матриц

Если - квадратная матрица, то матрица, обратная относительно нее и обозначаемая как , обладает следующими свойствам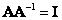и: и . Об этом говорит сайт https://intellect.icu . Если матрица существует, то матрица называется неособенной (невырожденной). В противном случае она называется особенной (вырожденной). Если у некоторой матрицы есть обратная, то эта обратная матрица единственна. Матрица, обратная относительной обратной, совпадает с исходной матрицей, т.е.

(5.1.7)

Если матрицы и неособенные, то

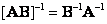(5.1.8)

Если матрица неособенная, а скаляр , то

. (5.1.9)

Обращение особенных квадратных матриц и неквадратных матриц будет рассмотрено в гл. 8. Матрицу, обратную относительно блочной квадратной матрицы

, (5.1.10)

можно представить в виде

(5.1.11)

при условии, что матрицы и не являются особенными.

Транспонирование матриц

При транспонировании матрицы размера 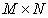образуется матрица размера , которую обозначают через . Строки матрицы совпадают со столбцами, а столбцы — со строками матрицы . Для любой матрицы

. (5.1.12)

Если , то матрицу называют симметричной. Для любых матриц и

(5.1.13)

Если матрица неособенная, то матрица также неособенная и

. (5.1.14)

Прямое произведение матриц

Левое прямое произведение матрицы размера на матрицу размера 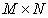представляет собой матрицу размера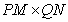

. (5.1.15)

Аналогично можно определить правое прямое произведение. В этой книге будет использоваться только левое прямое произведение. Прямые произведения и 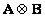могут различаться между собой. Ниже указаны свойства операций умножения, сложения, транспонирования и обращения прямого произведения матриц:

, (5.1.16)

, (5.1.17)

, (5.1.18)

, (5.1.18)

След матрицы

След квадратной матрицы размера равен сумме ее диагональных элементов и обозначается как

. (5.1.20)

Если и - квадратные матрицы, то

. (5.1.21)

След прямого произведения двух матриц равен

. (5.1.22)

Норма вектора

Евклидовой нормой вектора размера называется скаляр, определяемый как

. (5.1.23)

Норма матрицы

Евклидовой нормой матрицы размера 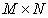называется скаляр, определяемый следующим образом:

. (5.1.24)

Ранг матрицы

Матрица размера имеет ранг , если наибольший из всех ее квадратных неособенных блоков имеет размер . Понятие о ранге используется при обращении матриц. Если матрицы и неособенные, а - произвольная матрица, то

. (5.1.25)

Ранг произведения матриц и удовлетворяет неравенствам

, (5.1.26а)

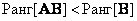. (5.1.26б)

Ранг суммы матриц и удовлетворяет неравенству

. (5.1.27)

Скалярное произведение векторов

Скалярным произведением векторов и размера является скаляр

(5.1.28)

или

. (5.1.29)

Матричное произведение векторов

Матричным произведением вектора размера на вектор размера является матрица

, (5.1.30)

где .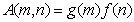

Квадратичная форма

Квадратичной формой вектора размера является скаляр

, (5.1.31)

где - матрица размера . Часто матрицу берут симметричной.

Векторная производная

Производная от скалярного произведения по есть

, (5.1.32)

а производная от скалярного произведения по вектору равна

. (5.1.33)

Производная от квадратичной формы по есть

. (5.1.34)

На рисунке 4.1,а-г приведены условные графики амплитудных спектров.

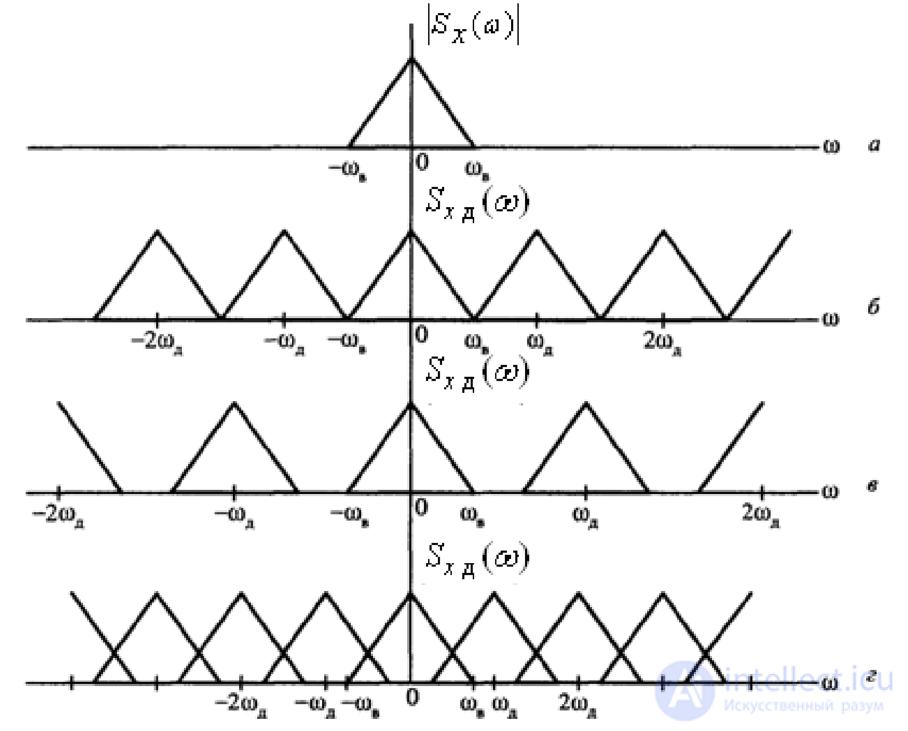
Рис. 4.1. Связь между спектрами аналогового и дискретного сигналов: а) аналогового сигнала с ограниченным по частоте спектром; б) дискретного сигнала при частотах

Вау!! 😲 Ты еще не читал? Это зря!

• Дискретные изображения

Надеюсь, эта статья об увлекательном мире математическое описание дискретных изображений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое математическое описание дискретных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про математическое описание дискретных изображений

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.