5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ

Привет, сегодня поговорим про модели плотностей вероятности дискретных изображений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое модели плотностей вероятности дискретных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Дискретное изображение, представленное массивом 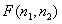, можно полностью описать с помощью совместной плотности вероятности его элементов. При задании в матричной форме эта плотность записывается как

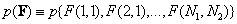,          (5.5.1а)

а в векторной форме - как

,                       (5.5.1б)

где 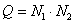 определяет порядок совместной плотности. Если все элементы изображения статистически независимы, то совместная плотность вероятности равна произведению одномерных безусловных плотностей

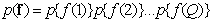.                 (5.5.2)

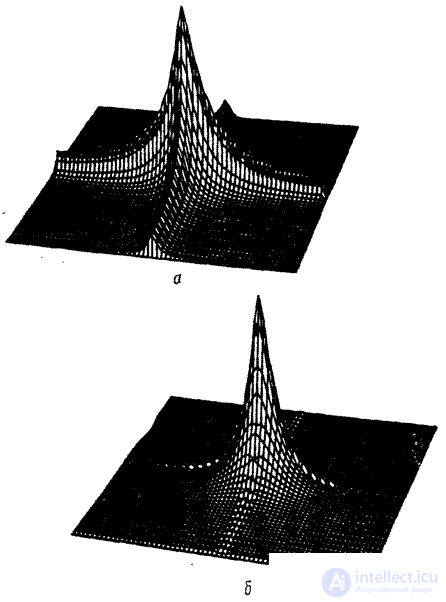
Рис. 5.4.2. Энергетические спектры марковских процессов, моделирующих изображения (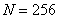, по вертикальной оси логарифмический масштаб): а – разделимый спектр; б – спектр с круговой симметрией.

Наиболее распространенным видом совместной плотности вероятности является гауссова плотность

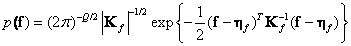,     (5.5.3)

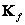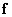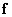где  - ковариационная матрица вектора ,  - среднее значение , а символом  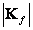обозначен определитель матрицы 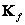. Гауссова плотность является полезной моделью совместной плотности вероятности коэффициентов, полученных в результате унитарных преобразований изображений. Однако гауссова плотность не подходит для описания яркости элементов изображения, поскольку яркость может быть только положительной, а гауссовы случайные величины принимают как положительные, так и отрицательные значения.

В литературе редко встречаются выражения для совместных плотностей, не являющихся гауссовыми. Хунс [13] разработал методику формирования подобных плотностей высокого порядка на основе заданной безусловной плотности первого порядка и заданной ковариационной матрицы элементов ансамбля. Для плотности с нулевым средним эта процедура сводится к линейному преобразованию набора независимых случайных величин , совместную плотность вероятности которых

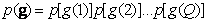       (5.5.4)

можно записать в виде произведения заданных плотностей первого порядка. Тогда искомая совместная плотность вероятности имеет вид

,                           (5.5.5)

где

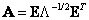,                                                (5.5.6)

а 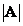 обозначает определитель матрицы 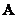. Об этом говорит сайт https://intellect.icu . Столбцы матрицы  являются собственными векторами заданной ковариационной матрицы 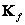, а матрица  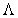- диагональная и состоит из собственных значений этой матрицы, причем выполняется соотношение

.                                     (5.5.7)

Рис. 5.5.1. Двумерные плотности вероятности пары коррелированных случайных величин : а – плотность распределения вероятностей Лапласа; б – плотность распределения вероятностей Рэлея.

На рис. 5.5.1 приведены двумерные плотности вероятности пары коррелированных случайных величин, безусловные распределения которых являются распределениями Рэлея или Лапласа. Многомерная модель с распределением Рэлея полезна при рассмотрении совместной плотности вероятности яркостей элементов изображения, а модель с распределением Лапласа применяется для статистического описания последовательности разностных сигналов, образующихся в системах кодирования изображений методом предсказания.

В следующей главе рассматривается методика квантования, т. е. представления отсчетов с помощью дискретного набора чисел, называемых уровнями квантования. Пусть 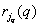 обозначает 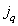-й уровень квантования для элемента изображения, который занимает -e место в векторе изображения 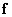. Тогда вероятность получения одного из возможных значений вектора  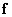можно выразить через совместное распределение вероятностей значений отсчетов следующим образом:

,      (5.5.8)

где . Обычно для всех компонент вектора выбирают одинаковый набор уровней квантования и совместное распределение вероятностей принимает вид

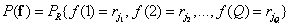.         (5.5.9)

Распределения вероятностей значений отсчетов можно оценить, измеряя соответствующие частоты. Так, одномерное распределение -й компоненты вектора

         (5.5.10)

можно оценить путем анализа большого набора изображений, относящихся к одному и тому же классу, таких, например, как флюорограммы, аэрофотоснимки полей и т. д. Оценкой одномерного распределения вероятностей служит распределение относительных частот

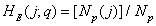,       (5.5.11)

где 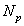 - полное число исследованных снимков, а  - число снимков, для которых 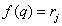,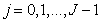. Если источник изображений является стационарным, то одномерные распределения (5.5.10) будут одинаковы для всех компонент вектора, т. е. не будут зависеть от . Кроме того, если источник изображений является эргодическим, то усреднение по ансамблю (измерения при использовании набора снимков) можно заменить усреднением по пространственным координатам. Если предположение об эргодичности справедливо, то одномерное распределение можно оценить по частотам

,                (5.5.12)

где  - число элементов исследуемого изображения, для которых 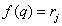, причем 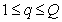, а .

На рис. 5.5.2 приведены одномерные гистограммы красной, зеленой и синей координат цвета цветного изображения «Портрет». В большинстве естественных изображений темных элементов гораздо больше, чем светлых, и частоты с ростом яркости убывают примерно по экспоненте.

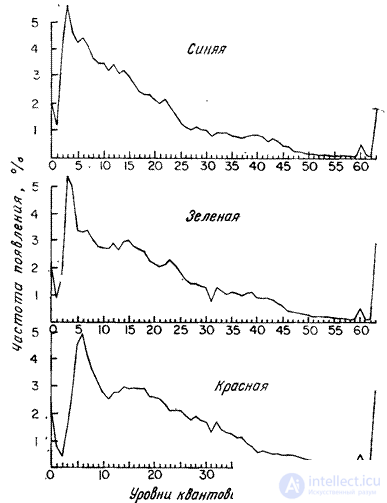
Рис. 5.5.2. Типичные гистограммы красной, зеленой и синей координат цвета цветного изображения.

Оценку двумерного распределения вероятностей для эргодического источника изображений можно найти с помощью распределения частот второго порядка, которые получают, подсчитывая случаи совместного появления определенных пар значений элементов, разделенных заданным расстоянием. Допустим, что 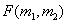 и 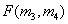 есть два элемента изображения, разделенные отрезком длиной 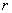, который наклонен к горизонтальной оси под углом  (рис. 5.5.3). Поскольку элементы образуют прямоугольную решетку, параметры 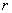,  могут принимать только некоторые дискретные значения. Относительная частота второго порядка есть

,      (5.5.13)

где  - число пар элементов изображения, для которых 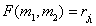 и 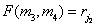. Знаменатель дроби (5.5.13)  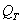представляет собой полное число пар элементов, которые разделены отрезками с одинаковыми параметрами 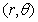. Из-за краевых эффектов .

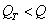Рис. 5.5.3. Взаимное расположение пары элементов изображения.

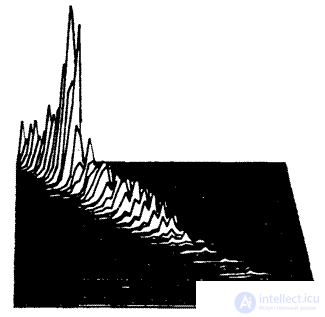
Рис. 5.5.4. Гистограммы второго порядка для изображения «Портрет».

Гистограммы второго порядка для изображения «Портрет» представлены на рис.5.5.4. Элементы изображения с увеличением расстояния между ними становятся менее коррелированными, и частоты распределяются по плоскости более равномерно.

Надеюсь, эта статья об увлекательном мире модели плотностей вероятности дискретных изображений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое модели плотностей вероятности дискретных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений