8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР

Привет, Вы узнаете о том , что такое обобщенный линейный оператор, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обобщенный линейный оператор , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

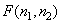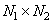Рассмотрим массив  из  элементов, представляющий исходное (входное) изображение. При воздействии на него обобщенным линейным оператором получается массив из  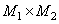элементов, описывающий преобразованное (выходное) изображение

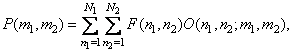     (8.1.1)

где ядро оператора 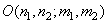 представляет собой набор весовых множителей, зависящих в общем случае от координат элементов как входного, так и выходного изображений.

При анализе линейных операций по обработке изображений удобно пользоваться векторными представлениями, описанными в гл. 5 [1]. Поэтому будем полагать, что входной массив 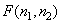 представлен или в виде матрицы 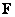, или в виде вектора 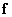, полученного разверткой матрицы  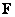по столбцам. Аналогичным образом допустим, что выходной массив  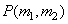может быть представлен либо матрицей 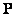, либо в виде ее развертки по столбцам, т. е. вектором 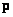. Для упрощения обозначений ниже будет принято, что матрицы, представляющие входное и выходное изображения, квадратные с размерами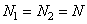   соответственно. Допустим теперь, что символ 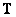 обозначает матрицу размера 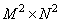, с помощью которой вектор исходного изображения  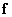размера  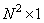линейно преобразуется в вектор

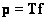                                   (8.1.2)

выходного изображения размера. Матрицу 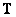 можно разделить на блоки - матрицы  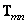размера  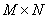(число которых также равно 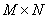) - и представить ее в следующем виде:

     (8.1.3)

В согласии с соотношением (5.3.3) вектор выходного изображения 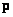 можно выразить через матрицу входного изображения :

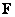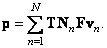                                (8.1.4)

Кроме того, с помощью равенства (5.3.4) матрицу 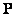 выходного изображения можно выразить через вектор p того же изображения:

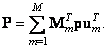                                (8.1.5)

Из этих формул получим выражение, связывающее между собой входную и выходную матрицы:

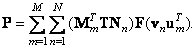          (8.1.6)

Заметим, что операторы 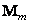 и 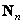 просто выделяют из матрицы  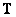блок 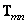. Об этом говорит сайт https://intellect.icu . Следовательно,

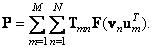                     (8.1.7)

Пусть линейное преобразование является разделимым, т. е. матрицу 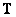 можно представить в виде прямого произведения

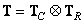                                      (8.1.8)

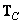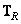где  и  - операторы преобразования столбцов и строк матрицы изображения 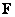. В этом случае

                                        (8.1.9)

Следовательно,

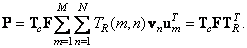     (8.1.10)

Таким образом, матрицу выходного изображения 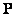 можно получить путем последовательной обработки матрицы  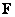по строкам и столбцам.

При обработке изображений во многих случаях оказывается, что оператор линейного преобразования 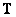 имеет специфическую структуру, позволяющую упростить вычислительные операции. Ниже перечислены важные частные случаи, проиллюстрированные на рис. 8.1.1, когда размеры входного и выходного изображений выбраны одинаковыми, т. е. .

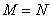а) При обработке матрицы 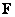 только по столбцам

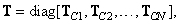              (8.1.11)

где 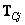 - матрица преобразования для 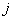-го столбца.

б) При одинаковой обработке каждого столбца матрицы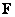 

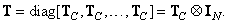              (8.1.12)

в) При обработке матрицы 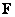 только по строкам

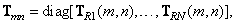            (8.1.13)

где 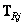 - матрица преобразования для 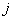-й строки.

г) При одинаковой обработке каждой строки матрицы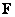 

  (8.1.14a)

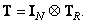                                                 (8.1.14б)

д) При одинаковой обработке столбцов и одинаковой обработке строк матрицы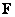 

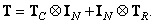                                 (8.1.15)

Число арифметических операций, выполняемых в каждом из этих случаев, указано в табл. 8.1.1.

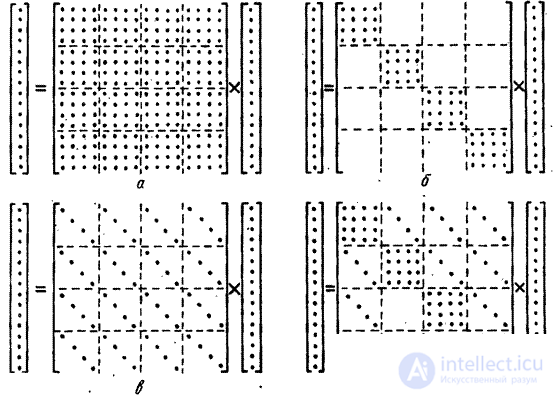
Рис. 8.1.1. Структура матриц линейного оператора: а – общий случай; б – обработка только по столбцам; в – обработка только строкам; г – обработка только строкам и столбцам.

Таблица 8.1.1. Число арифметических операций при линейном преобразовании

Из соотношения (8.1.10) видно, что если двумерное линейное преобразование имеет разделимую матрицу, то его можно выполнить путем последовательной одномерной обработки строк и столбцов массива отсчетов. Как следует из табл. 8.1.1, для таких преобразований удается существенно сократить число необходимых вычислительных операций: в общем случае при вычислении по формуле (8.1.2) требуется  операций, но если можно воспользоваться формулой (8.1.10), достаточно 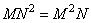 операций. Более того, в этом случае матрицу  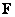можно хранить в запоминающем устройстве (ЗУ) с последовательным доступом, например на диске или на барабане, и считывать строка за строкой, т. е. отпадает необходимость хранения матрицы  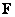в более дорогостоящем ЗУ с произвольным доступом. Необходимо, однако, транспонировать результаты преобразований по столбцам с тем, чтобы выполнить построчные преобразования. В работах [2, 3] описаны алгоритмы транспонирования матриц, записанных в ЗУ с последовательным доступом.

Выводы из данной статьи про обобщенный линейный оператор указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое обобщенный линейный оператор и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений