8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Привет, Вы узнаете о том , что такое решение совместных систем линейных уравнений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое решение совместных систем линейных уравнений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Установив существование решения системы уравнений

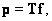                                             (8.5.1)

следует определить характер решения: является ли оно единственным или же решений несколько, а также какой вид имеет решение? Ответ на последний вопрос содержится в следующей фундаментальной теореме [4]:

Если решение системы уравнений 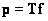 существует, то в общем случае оно имеет вид

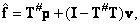                (8.5.2)

где 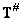 - матрица, условно обратная относительно матрицы 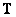, a 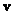 - произвольный вектор размера .

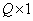Для доказательства умножим обе части соотношения (8.5.2) на матрицу :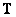

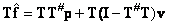     (8.5.3)

Однако по условию существования решения 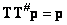. Кроме того, согласно определению условно обратной матрицы, 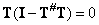. Следовательно,  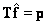и вектор  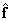является решением.

Поскольку 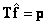, то, умножив обе части этого равенства на матрицу 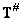, получим

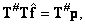                                  (8.5.4а)

или

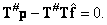                           (8.5.4б)

Прибавив к обеим частям вектор 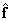, получим

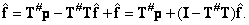     (8.5.5)

Этот результат совпадает с соотношением (8.5.2), если вектор 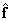, стоящий в правой части формулы (8.5.5), заменить на произвольный вектор .

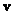Поскольку обобщенная обратная матрица 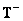 и матрица  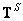обращения методом наименьших квадратов являются условно обратными, то общее решение системы (8.5.1) также можно представить в виде

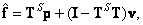     (8.5.6а)

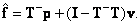     (8.5.6б)

Решение очевидно, будет единственным, если 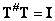. Об этом говорит сайт https://intellect.icu . Bo всех подобных случаях 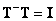. Исследовав ранг матрицы 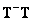, можно доказать, что [4] если решение системы уравнений  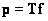существует, что оно единственно тогда и только тогда, когда ранг матрицы  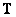размера  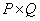равен .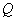

Отсюда следует, что если решение недоопределенной системы уравнений существует, то оно не единственно. С другой стороны, переопределенная система уравнений может иметь только одно решение.

Пусть для системы уравнений (8.5.1) может быть получено точное решение. Рассмотрим оценку

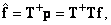     (8.5.7)

где 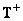 обозначает одну из матриц, псевдообратных относительно 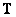, которая не обязательно будет совпадать с этим решением, поскольку произведение матриц  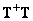может не равняться единичной матрице. Величину ошибки, т. е. отклонение оценки  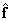от истинного значения 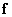, обычно выражают через квадрат разности векторов  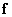и 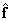 в виде произведения

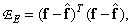                   (8.5.8а)

или как

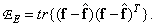           (8.5.8б)

Подставив выражение (8.5.7) в (8.5.8а), получим

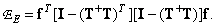     (8.5.9)

Значение матрицы 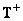, при котором ошибка (8.5.8) оказывается минимальной, можно найти, приравняв нулю производную от ошибки  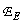по вектору 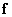. Согласно соотношению (5.1.34),

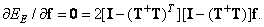     (8.5.10)

Равенство (8.5.10) удовлетворяется, если матрица , т. е. является обобщенной обратной матрицей относительно 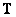. При этом ошибка оценивания уменьшается до минимума, равного

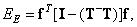                 (8.5.11а)

или

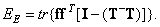     (8.5.11б)

Как и ожидалось, ошибка становится равной нулю, когда 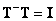. Это произойдет, например, если обобщенная обратная матрица  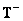имеет ранг  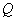и определяется соотношением (8.3.5

Выводы из данной статьи про решение совместных систем линейных уравнений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое решение совместных систем линейных уравнений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений