Лекция
Привет, Вы узнаете о том , что такое оператор циклической суперпозиции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое оператор циклической суперпозиции , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
При использовании оператора циклической суперпозиции массивы отсчетов входного и выходного изображений, а также импульсного отклика должны быть периодическими по пространственным переменным с одинаковым периодом. Для единства изложения примем, как и прежде, что все эти массивы имеют конечные размеры. Допустим также, что массив исходных отсчетов  размером
размером 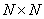 помещен в левый верхний угол массива, содержащего
помещен в левый верхний угол массива, содержащего  нулей
нулей 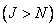 , т. е. образуется расширенный массив
, т. е. образуется расширенный массив
 при
при 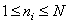 , (9.3.1а)
, (9.3.1а)
 при
при  . (9.3.1б)
. (9.3.1б)
Аналогично формируется расширенный массив отсчетов импульсного отклика:
 при
при  , (9.3.2а)
, (9.3.2а)
 при
при  . (9.3.2б)
. (9.3.2б)
Далее образуем периодически продолженные массивы  и
и 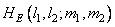 , повторяя (размножая) расширенные массивы с периодом в
, повторяя (размножая) расширенные массивы с периодом в  отсчетов. Циклическая свертка этих массивов по определению равна
отсчетов. Циклическая свертка этих массивов по определению равна
 . (9.3.3)
. (9.3.3)
Бросается в глаза сходство данного выражения с равенством (9.1.1), описывающим суперпозицию конечных массивов. Об этом говорит сайт https://intellect.icu . В самом деле, если  выбрано так, что
выбрано так, что  , то
, то  при
при  . Следует также отметить сходство циклической суперпозиции с суперпозицией дискретизованных массивов. Эти соотношения становятся более ясными, когда используется векторное представление циклической суперпозиции.
. Следует также отметить сходство циклической суперпозиции с суперпозицией дискретизованных массивов. Эти соотношения становятся более ясными, когда используется векторное представление циклической суперпозиции.
Допустим, что массивы 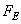 и
и  представлены соответственно
представлены соответственно 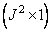 -компонентными векторами
-компонентными векторами  и
и  . Тогда для операции циклической суперпозиции можно записать соотношение
. Тогда для операции циклической суперпозиции можно записать соотношение
 , (9.3.4)
, (9.3.4)
где  - матрица элементов массива
- матрица элементов массива  размера
размера  .
оператор циклической суперпозиции удобно выразить в виде блочной матрицы с блоками
.
оператор циклической суперпозиции удобно выразить в виде блочной матрицы с блоками  размера
размера  :
:
 , (9.3.5)
, (9.3.5)
где
 , (9.3.6)
, (9.3.6)
причем  и
и 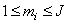 , a
, a 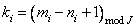 и
и  . Следует отметить, что каждая строка и каждый столбец блочной матрицы
. Следует отметить, что каждая строка и каждый столбец блочной матрицы  содержат
содержат  ненулевых блоков. Если массив отсчетов импульсного отклика является пространственно-инвариантным, то
ненулевых блоков. Если массив отсчетов импульсного отклика является пространственно-инвариантным, то
 (9.3.7)
(9.3.7)
и любую строку (или столбец) можно получить путем циклической перестановки блоков первой строки (или первого столбца). На рис. 9.3.1,а приведен пример оператора циклической свертки, когда входной и выходной массивы имеют размеры 
 , а размер массива отсчетов импульсного отклика равен
, а размер массива отсчетов импульсного отклика равен 
 . На рис. 9.3.1,б показана структура матрицы того же оператора при
. На рис. 9.3.1,б показана структура матрицы того же оператора при 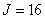 и
и  , когда импульсный отклик имеет гауссову форму.
, когда импульсный отклик имеет гауссову форму.

Рис. 9.3.1. Примеры матриц оператора циклической свертки.
а - общий случай, 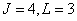 ; б - импульсный отклик гауссовой формы,
; б - импульсный отклик гауссовой формы,  .
.
Если же импульсный отклик является пространственно-инвариантным и разделимым, то
 , (9.3.8)
, (9.3.8)
где  и
и  - матрицы вида
- матрицы вида
 , (9.3.9)
, (9.3.9)
размер которых равен  . При этом двумерная циклическая свертка вычисляется в соответствии с соотношением
. При этом двумерная циклическая свертка вычисляется в соответствии с соотношением
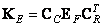 . (9.3.10)
. (9.3.10)
Выводы из данной статьи про оператор циклической суперпозиции указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое оператор циклической суперпозиции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про оператор циклической суперпозиции
Комментарии
Оставить комментарий
Цифровая обработка изображений
Термины: Цифровая обработка изображений