Лекция
Привет, сегодня поговорим про интерполяционные функции, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое интерполяционные функции , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
На рис. 4.3.4 приведены примеры одномерных интерполяционных функций. Как уже отмечалось, функция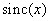 
обеспечивает точное восстановление, но, как правило, ее трудно сформировать в реальной системе воспроизведения изображений. Простейшей интерполяционной функцией является прямоугольная функция, с помощью которой осуществляется интерполяция отсчетов многочленом нулевого порядка. Треугольная функция обеспечивает линейную интерполяцию первого порядка. Подобную функцию можно рассматривать как свертку двух прямоугольных функций. Свертка треугольной функции с прямоугольной дает колоколообразную интерполяционную функцию, изображенную на рис. 4.3.4, г. Повторением этого процесса можно быстро прийти к гауссовой интерполяционной функции, приведенной на рис. 4.3.4, е. Многочлены второго и более высокого порядка также пригодны для интерполяции отсчетов. Особенно удобным для интерполяции изображений является кубический B-сплайн, поскольку в результате интерполяции получается функция, непрерывная и гладкая в узлах интерполяции.
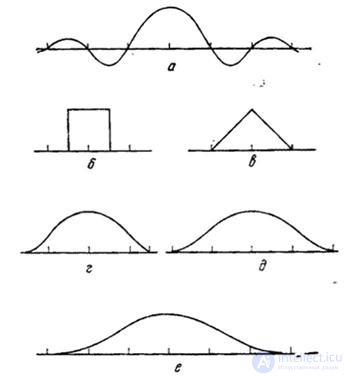
Рис. 4.3.4. Одномерные
интерполяционные функции : а - 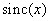; б – прямоугольная; в - треугольная (свертка двух прямоугольных функций); г - колоколообразная (свертка трех прямоугольных функций); д - кубический B-cплайи (свертка четырех прямоугольных функций); e - гауссова
Кубический B-сплайн определяется [14] соотношением
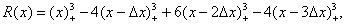(4.3.1)
где
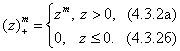
Эту функцию, отличную от нуля только на четырех интервалах дискретизации, можно получить, выполнив сверткучетырех прямоугольных функций. Об этом говорит сайт https://intellect.icu . Рис. 4.3.5 иллюстрирует процесс одномерной интерполяции с использованием функций 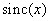, а также прямоугольных и треугольных функций.
В табл. 4.3.1 даны определения нескольких двумерных разделимых интерполяционных функций, для которых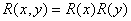 
. Следует отметить, что операция двумерной линейной интерполяции (или интерполяция многочленами первого порядка), аналогичная операции одномерной линейной интерполяции (рис. 4.3.5, в), отличается от интерполяции с помощью двумерных треугольных функций, представленных в табл. 4.3.1. Эту операцию следует выполнять кусочно-линейным способом, как показано на рис. 4.3.6, а. В области I отсчеты линейно интерполируются плоскостью, заданной точками А, В и С, тогда как в области II они линейно интерполируются плоскостью, заданной точками В, С и D. Непрерывный билинейный способ интерполяции, иллюстрируемый на рис. 4.3.6, б, сводится к последовательной линейной интерполяции между парами точек, расположенных на прямых, параллельных осям координат. В результате образуется некоторая поверхность, проходящая через точки А, В, С и D (см. рис. 4.3.6, б). Как правило, эта поверхность оказывается неплоской.
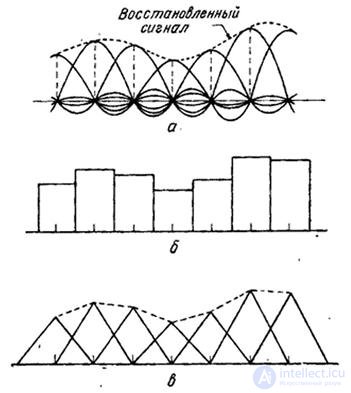
Рис.4.3.5. Одномерная интерполяция: а – функция 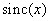; б – прямоугольные функции (интерполяция нулевого порядка); в – треугольные функции (интерполяция первого порядка).
Таблица 4.8.1. Двумерные разделимые интерполяционные функции
|
Функция |
Определение |
 |
|
|
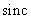Прямоугольная |
|
|
Треугольная |
|
|
Колоколообразная |
|
|
Кубический В-сплайн |
|
|
Гауссова |
|
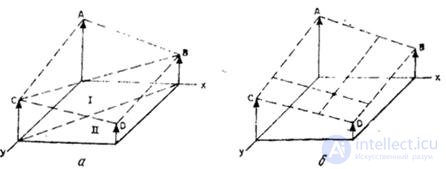
Рис. 4.3.6. Двумерная линейная интерполяция: а - кусочно-линейная интерполяция; б - билинейная интерполяция.
Надеюсь, эта статья об увлекательном мире интерполяционные функции, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое интерполяционные функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про интерполяционные функции
Комментарии