Лекция
Привет, сегодня поговорим про верность воспроизведения одноцветных изображений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое верность воспроизведения одноцветных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
Построению и развитию системы количественных мер верности воспроизведения одноцветных изображений уделялось большое внимание [27-32]. Разумные меры верности должны хорошо согласовываться с результатами субъективных оценок для широкого класса изображений, не требуя при этом чересчур сложных вычислений. Кроме того, желательно, чтобы эти меры имели простую аналитическую форму и их можно было бы применять в качестве критериев оптимальности при оптимизации или выборе параметров систем обработки изображений.
Количественные меры верности воспроизведения одноцветных изображений можно разделить на две группы: одиночные и парные. Одиночная мера представляет собой число, сопоставляемое любому изображению на основе анализа его структуры. Парная мера является числовым результатом взаимного сравнения двух изображений.
Измерения верности в цифровой системе обработки изображений можно провести, используя либо непрерывное изображение, сформированное из массива отсчетов, либо сам этот массив. Обычно предпочитают второй способ, так как он проще с практической точки зрения. Однако, для того чтобы измерения на массиве отсчетов согласовывались с результатами субъективных оценок, воспроизводящее устройство не должно создавать больших или по крайней мере непредсказуемых искажений изображения. Ниже сначала будут введены меры верности изображений, получаемые на основе непрерывных двумерных функций, а затем представлены их дискретные варианты и описано соотношение между ними.
Рассмотрим непрерывную функцию 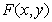 , описывающую изображение, которая определена в прямоугольной области
, описывающую изображение, которая определена в прямоугольной области 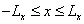 ,
, 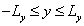 . Предположим, что эта функция получена путем двумерной интерполяции массива отсчетов изображения
. Предположим, что эта функция получена путем двумерной интерполяции массива отсчетов изображения 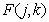
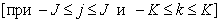 согласно соотношению
согласно соотношению
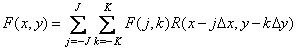 , (7.4.1)
, (7.4.1)
где 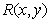 — непрерывная интерполяционная функция, а
— непрерывная интерполяционная функция, а 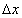 и
и 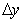 — шаги дискретизации.
— шаги дискретизации.
Одиночную оценку верности в общем виде можно представить соотношением
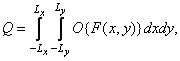 (7.4.2)
(7.4.2)
где 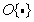 — некоторый (возможно, нелинейный) оператор. Критерии верности часто формулируют с использованием преобразований Фурье. В таком случае обобщенная форма одиночной меры верности имеет вид
— некоторый (возможно, нелинейный) оператор. Критерии верности часто формулируют с использованием преобразований Фурье. В таком случае обобщенная форма одиночной меры верности имеет вид
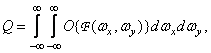 (7.4.3)
(7.4.3)
где 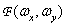 — непрерывный двумерный спектр Фурье изображения
— непрерывный двумерный спектр Фурье изображения 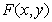 . Одна из наиболее простых мер подобного рода — предложенное Штрелем [33, стр. 461] отношение
. Одна из наиболее простых мер подобного рода — предложенное Штрелем [33, стр. 461] отношение
 (7.4.4)
(7.4.4)
где 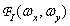 — спектр исходного изображения. Первоначально это отношение использовалось для оценки качества элементов оптических систем. Спектральные составляющие оптического изображения в некоторой реальной оптической системе обычно уменьшаются по величине и, возможно, изменяются по фазе по сравнению с теми же составляющими в идеальной (безаберрационной) оптической системе, свойства которой ограничиваются только дифракционными явлениями. Составляющие с высокими пространственными частотами, как правило, ослабляются в наибольшей степени. С учетом определения преобразования Фурье (1.6.6а) отношение Штреля (7.4.4) сводится к
— спектр исходного изображения. Первоначально это отношение использовалось для оценки качества элементов оптических систем. Спектральные составляющие оптического изображения в некоторой реальной оптической системе обычно уменьшаются по величине и, возможно, изменяются по фазе по сравнению с теми же составляющими в идеальной (безаберрационной) оптической системе, свойства которой ограничиваются только дифракционными явлениями. Составляющие с высокими пространственными частотами, как правило, ослабляются в наибольшей степени. С учетом определения преобразования Фурье (1.6.6а) отношение Штреля (7.4.4) сводится к 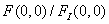 , т. е. к отношению центральных отсчетов реального и идеального изображений. Таким образом, отношение Штреля по существу является простой мерой уменьшения контраста реального изображения по сравнению с идеальным. Отношение Штреля в некоторой степени соответствует субъективным представлениям о качестве изображения, однако эксперименты показывают, что это соответствие не всегда полное. В частности, известны примеры изображений, которые обладали достаточно высокой дешифрируемостью, несмотря на то что отношение Штреля для них было небольшим [34].
, т. е. к отношению центральных отсчетов реального и идеального изображений. Таким образом, отношение Штреля по существу является простой мерой уменьшения контраста реального изображения по сравнению с идеальным. Отношение Штреля в некоторой степени соответствует субъективным представлениям о качестве изображения, однако эксперименты показывают, что это соответствие не всегда полное. В частности, известны примеры изображений, которые обладали достаточно высокой дешифрируемостью, несмотря на то что отношение Штреля для них было небольшим [34].
Другим классическим примером одиночной меры верности изображения служит величина эквивалентного прямоугольника пропускания, равная по определению [35]
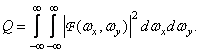 (7.4.5)
(7.4.5)
При возведении в квадрат возрастает вес составляющих изображения с низкими пространственными частотами, поскольку они, как правило, имеют большую величину. Однако и эта мера также не очень хорошо согласуется с результатами субъективных испытаний.
Попытки создания парных мер качества изображения имели несколько больший успех. Рассмотрим пару изображений, состоящую из некоторого эталонного (или идеального) изображения 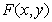 и его искаженного варианта
и его искаженного варианта  . Одной из мер «близости» двух изображений является их взаимная корреляция, равная по определению
. Одной из мер «близости» двух изображений является их взаимная корреляция, равная по определению
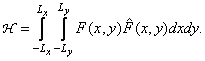 (7.4.6)
(7.4.6)
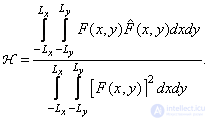
Обычно взаимную корреляцию нормируют относительно энергии эталонного изображения так, чтобы ее максимальное значение равнялось единице. Нормированная взаимно-корреляционная мера — коэффициент корреляции — имеет вид
 (7.4.7)
(7.4.7)
Согласно теореме Парсеваля (1.6.16), значения коэффициента корреляции можно вычислить по спектрам на основе соотношения
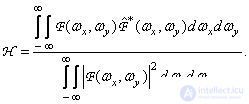 (7.4.8)
(7.4.8)
При восприятии изображений важную роль играют контуры предметов. Об этом говорит сайт https://intellect.icu . Поэтому Эндрюс [36] предложил пользоваться коэффициентом корреляции лапласианов изображений, определяемым как
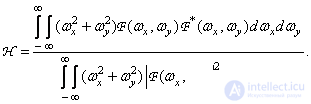 (7.4.9)
(7.4.9)
Напомним, что в силу соотношения (1.6.19) умножение спектра 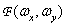 на квадрат частоты эквивалентно применению оператора Лапласа, что приводит к обострению контуров изображения, описываемого функцией
на квадрат частоты эквивалентно применению оператора Лапласа, что приводит к обострению контуров изображения, описываемого функцией  . Эксперименты, выполненные Эндрюсом на изображениях, которые были преобразованы с помощью фильтров низких и высоких пространственных частот, показывают, что обычный коэффициент корреляции остается довольно большим даже в том случае, когда очень сильно подавлены высоко- и среднечастотные компоненты изображения и субъективно оно воспринимается как низкокачественное, а коэффициент корреляции лапласианов быстро уменьшается при сужении полосы низкочастотного фильтра. Можно, однако, получить низкокачественные изображения с большими искажениями в области низких пространственных частот, для которых коэффициент корреляции лапласианов оказывается сравнительно большим.
. Эксперименты, выполненные Эндрюсом на изображениях, которые были преобразованы с помощью фильтров низких и высоких пространственных частот, показывают, что обычный коэффициент корреляции остается довольно большим даже в том случае, когда очень сильно подавлены высоко- и среднечастотные компоненты изображения и субъективно оно воспринимается как низкокачественное, а коэффициент корреляции лапласианов быстро уменьшается при сужении полосы низкочастотного фильтра. Можно, однако, получить низкокачественные изображения с большими искажениями в области низких пространственных частот, для которых коэффициент корреляции лапласианов оказывается сравнительно большим.
Еще одним парным критерием верности изображений является нормированная абсолютная ошибка — разность функций, описывающих эталонное и искаженное изображения:
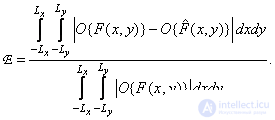 (7.4.10)
(7.4.10)
При обработке изображений в качестве меры ошибки чаще всего применяется нормированная среднеквадратическая ошибка, равная
 (7.4.11)
(7.4.11)
На практике обычно предпочитают пользоваться среднеквадратической, а не абсолютной ошибкой, поскольку первая удобнее для анализа, чем вторая. Именно поэтому проводились усиленные поиски таких преобразований, при которых среднеквадратическая ошибка преобразованной функции была бы хорошо согласована с субъективными оценками. В основном, конечно, рассматривались пространственные линейные и поэлементные нелинейные преобразования. Довольно много внимания уделялось степенным, а также логарифмическим преобразованиям. Исследовались операторы линейных пространственных преобразований, такие, как оператор градиента, оператор Лапласа и оператор свертки. Кроме того, рассматривались комбинации вышеупомянутых поэлементных и пространственных преобразований.
Выражение для ошибки можно также представить с помощью спектральных характеристик. В этом случае нормированная среднеквадратическая ошибка определяется соотношением
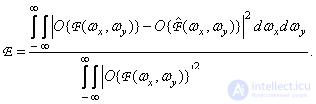 (7.4.12)
(7.4.12)
Интересный частный случай линейного преобразования — это частотное взвешивание, когда
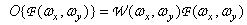 , (7.4.13)
, (7.4.13)
где 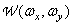 — весовая функция. Выражение для частотно-взвешенной среднеквадратической ошибки получается в виде
— весовая функция. Выражение для частотно-взвешенной среднеквадратической ошибки получается в виде
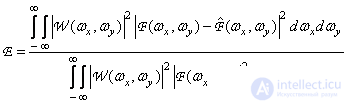 . (7.4.14)
. (7.4.14)
Следует отметить, что формула (7.4.14) совершенно эквивалентна выражению (7.4.11) для среднеквадратической ошибки, если оператор 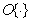 соответствует свертке, осуществляемой линейным фильтром с частотной характеристикой
соответствует свертке, осуществляемой линейным фильтром с частотной характеристикой
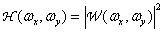
Уайлдер [37] провел глубокое исследование свойств абсолютной и среднеквадратической ошибок в дискретной форме применительно к степенному, логарифмическому и градиентному преобразованиям, а также к преобразованию Лапласа. Искаженные образцы изображений получались моделированием процесса кодирования исходного изображения с помощью различных алгоритмов. Было выяснено, что поэлементные преобразования в сочетании с критериями абсолютной и среднеквадратической ошибок не позволяют получить критерия верности, согласующегося с субъективными оценками. Меры ошибки, основанные на преобразовании Лапласа и градиентном преобразовании, имеют наибольшую корреляцию с субъективными оценками, но коэффициент корреляции не превышает 0,8, т. е. и эти критерии недостаточно надежны.
Большинство попыток найти приемлемые критерии верности изображения относится к частным случаям. Предлагается некий критерий, основанный на каких-то физиологических предпосылках, а чаще просто удобный для анализа и вычислений, а затем оцениваются его свойства. Другой подход к проблеме состоит в копировании процесса выработки оценки человеком, т. е. свойства изображения должны измеряться в той метрике, которая присуща человеческому мозгу. При таком подходе оцениваемое изображение сначала проходит предварительную обработку и только потом оценивается его верность. При этом аппроксимируются, насколько это возможно, процессы, фактически происходящие в начальных звеньях зрительной системы человека. В гл. 2 была описана модель входного каскада зрительной системы человека, состоящая из трех звеньев. Двумерная линейная система с импульсным откликом 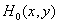 представляет оптические элементы глаза. Звено, выполняющее поэлементное нелинейное преобразование
представляет оптические элементы глаза. Звено, выполняющее поэлементное нелинейное преобразование 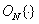 , моделирует отклик фоторецепторов. Вторая двумерная система с импульсным откликом
, моделирует отклик фоторецепторов. Вторая двумерная система с импульсным откликом  описывает процесс латерального торможения. Преобразование, выполняемое всей моделирующей системой, описывается выражением
описывает процесс латерального торможения. Преобразование, выполняемое всей моделирующей системой, описывается выражением
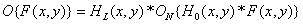 . (7.4.16)
. (7.4.16)
Маннос и Сакрисон [2] провели обширные измерения для разработки надежного среднеквадратического критерия верности одноцветных изображений, опирающегося на модель зрительной системы человека. Эффекты в оптической системе глаза, приводящие к ухудшению его разрешающей способности, при этом не учитывались, и соотношение (7.4.16) приводилось к более простому виду:
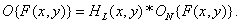 (7.4.17)
(7.4.17)
В этих экспериментах исходное распределение интенсивности, описывающее исходное изображение, подвергалось поэлементному нелинейному преобразованию по степенному или логарифмическому закону, а затем — пространственной фильтрации с частотной характеристикой
 (7.4.18)
(7.4.18)
где 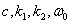 — постоянные. Далее в полученное изображение вносились искажения, эквивалентные возникающим в процессе оптимального кодирования с заданным средним числом двоичных разрядов на элемент изображения. Затем искаженное изображение подвергалось обратной пространственной фильтрации с частотной характеристикой
— постоянные. Далее в полученное изображение вносились искажения, эквивалентные возникающим в процессе оптимального кодирования с заданным средним числом двоичных разрядов на элемент изображения. Затем искаженное изображение подвергалось обратной пространственной фильтрации с частотной характеристикой  и обратному поэлементному нелинейному преобразованию. В результате получалось искаженное изображение в виде распределения интенсивности. Все эти операции выполнялись над дискретным изображением. Подобная процедура повторялась для различных изображений при разных значениях среднего числа двоичных разрядов и других параметров. Качество полученных изображений оценивалось субъективно по семибалльной шкале места в группе (табл. 7.1.2) и ранжированием. Оказалось, что при одинаковом среднем числе двоичных разрядов на элемент наивысшие оценки и места в группе получили те изображения, которые подвергались действию фильтра с частотной характеристикой, приведенной на рис. 7.4.1. Кроме того, нелинейное преобразование по степенному закону с показателем 1/3 дало гораздо лучшие результаты, чем логарифмическое преобразование. Исследования Манноса и Сакрисона показали также, что предварительная обработка согласно равенству (7.4.17), выполненная перед кодированием изображения, создает более благоприятные условия для кодирования. Результаты этих исследований удостоверяют еще и полезность применения среднеквадратического критерия верности с метрикой «геодезического пространства», характерного для человеческого зрения. Для количественного изучения этого критерия верности необходимы дальнейшие исследования.
и обратному поэлементному нелинейному преобразованию. В результате получалось искаженное изображение в виде распределения интенсивности. Все эти операции выполнялись над дискретным изображением. Подобная процедура повторялась для различных изображений при разных значениях среднего числа двоичных разрядов и других параметров. Качество полученных изображений оценивалось субъективно по семибалльной шкале места в группе (табл. 7.1.2) и ранжированием. Оказалось, что при одинаковом среднем числе двоичных разрядов на элемент наивысшие оценки и места в группе получили те изображения, которые подвергались действию фильтра с частотной характеристикой, приведенной на рис. 7.4.1. Кроме того, нелинейное преобразование по степенному закону с показателем 1/3 дало гораздо лучшие результаты, чем логарифмическое преобразование. Исследования Манноса и Сакрисона показали также, что предварительная обработка согласно равенству (7.4.17), выполненная перед кодированием изображения, создает более благоприятные условия для кодирования. Результаты этих исследований удостоверяют еще и полезность применения среднеквадратического критерия верности с метрикой «геодезического пространства», характерного для человеческого зрения. Для количественного изучения этого критерия верности необходимы дальнейшие исследования.

Рис. 7.4.1. Характеристики 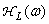 и
и  , обеспечивающие наилучшее субъективное качество изображений при моделировании процесса кодирования [2]: а – частотная характеристика; б – характеристика поэлементного нелинейного преобразования.
, обеспечивающие наилучшее субъективное качество изображений при моделировании процесса кодирования [2]: а – частотная характеристика; б – характеристика поэлементного нелинейного преобразования.
В системах цифровой обработки изображений для определения верности воспроизведения обычно гораздо удобнее использовать дискретные отсчеты, а не аналоговые изображения. Поэтому важно найти критерии верности на основе дискретных отсчетов, которые хорошо согласуются с результатами субъективных оценок непрерывных изображений.
Непосредственный способ получения таких критериев верности состоит в простой «дискретизации» соответствующих аналоговых критериев. Так, например, нормированную среднеквадратическую ошибку (НСКО), описывающую различие между отсчетами 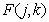 непрерывного эталонного изображения
непрерывного эталонного изображения 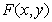 и отсчетами
и отсчетами 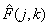 непрерывного искаженного изображения
непрерывного искаженного изображения 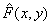 , можно представить как
, можно представить как
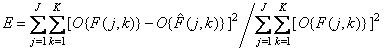 . (7.4.19)
. (7.4.19)
Можно показать, что эта мера совпадает с соответствующей «непрерывной» мерой, описываемой соотношением (7.4.11), если при дискретизации обоих изображений удовлетворяется критерий Найквиста. К сожалению, в реальных системах обработки изображений отсчеты, на основе которых создается воспроизводимое непрерывное изображение, не являются его найквистовскими отсчетами, так как воспроизводящее устройство вносит свои искажения и в нем трудно осуществить оптимальную двумерную интерполяцию. Тем не менее необходимость часто вынуждает пользоваться характеристиками, подобными (7.4.19), даже в тех случаях, когда они неточны.
В табл. 7.4.1 указаны некоторые наиболее распространенные критерии верности, основанные на оценках нормированных среднеквадратических ошибок (НСКО) для дискретных изображений. Еще одним широко применяемым критерием верности является так называемая пиковая среднеквадратическая ошибка (ПСКО), определяемая соотношением
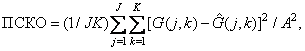 (7.4.20)
(7.4.20)
где 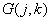 — преобразованное изображение, соответствующее определению, приведенному в табл. 7.4.1, а число
— преобразованное изображение, соответствующее определению, приведенному в табл. 7.4.1, а число 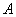 равно максимальному значению
равно максимальному значению 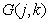 . Среднеквадратические ошибки часто измеряют в децибелах и рассматривают как отношение сигнал/шум (С/Ш):
. Среднеквадратические ошибки часто измеряют в децибелах и рассматривают как отношение сигнал/шум (С/Ш):
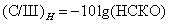 (7.4.21a)
(7.4.21a)
или
 (7.4.21б)
(7.4.21б)
Таблица 7.4.1. Критерии верности, основанные на оценках нормированных среднеквадратических ошибок, для дискретных одноцветных изображений
|
Без преобразования
|
|
С поэлементным преобразованием
|
|
Степенной закон
|
|
Логарифмический закон
|
|
С преобразованием Лапласа
где
|
|
С использованием свертки
где
|
Имея дело с операторами пространственных преобразований, такими, как оператор Лапласа или оператор свертки (табл. 7.4.1), не следует забывать, что массивы отсчетов изображений имеют конечные размеры. Поэтому пределы суммирования [в выражениях, подобных (7.4.19) или (7.4.20)] необходимо ограничивать центральными областями массивов 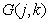 и
и 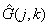 с тем, чтобы избежать краевых эффектов, которые появляются при аппроксимации непрерывных интегралов свертки дискретными суммами. Более подробно эти вопросы рассматриваются в гл. 11.
с тем, чтобы избежать краевых эффектов, которые появляются при аппроксимации непрерывных интегралов свертки дискретными суммами. Более подробно эти вопросы рассматриваются в гл. 11.
Надеюсь, эта статья об увлекательном мире верность воспроизведения одноцветных изображений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое верность воспроизведения одноцветных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Цифровая обработка изображений
Термины: Цифровая обработка изображений