Лекция
Привет, сегодня поговорим про квантование изображений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое квантование изображений, квантование скалярных величин , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
Любая аналоговая величина, подлежащая обработке в компьютере или цифровой системе, должна быть представлена в виде целого числа, пропорционального значению этой величины. Процесс преобразования отсчетов, имеющих непрерывное множество значений, в отсчеты с дискретными значениями называется квантованием. В следующих двух разделах дан математический анализ процесса квантования, который справедлив не только для изображений, но и вообще для широкого класса сигналов, с которыми приходится сталкиваться в системах обработки изображений. Затем рассматривается обработка квантованных отсчетов. В двух последних разделах описаны субъективные эффекты, возникающие при квантовании одноцветных и цветных изображений.
Квантование (англ. quantization) — в обработке сигналов — разбиение диапазона отсчетных значений сигнала на конечное число уровней и округление этих значений до одного из двух ближайших к ним уровней . При этом значение сигнала может округляться либо до ближайшего уровня, либо до меньшего или большего из ближайших уровней в зависимости от способа кодирования . Такое квантование называется скалярным. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей и замена этих значений идентификатором одной из этих областей.
Квантование , связанное с обработкой изображений , представляет собой метод сжатия с потерями , достигаемый путем сжатия диапазона значений до одного квантового значения. Когда количество дискретных символов в данном потоке уменьшается, поток становится более сжимаемым. Например, уменьшение количества цветов, необходимых для представления цифрового изображения, позволяет уменьшить размер его файла. Конкретные приложения включают квантование данных DCT в JPEG и квантование данных DWT в JPEG 2000 .
Поскольку квантование - это отображение многие-к-немногим, это по своей сути нелинейный и необратимый процесс (т. Е. Поскольку одно и то же выходное значение используется несколькими входными значениями, в общем случае невозможно восстановить точное входное значение, когда учитывая только выходное значение).
Набор возможных входных значений может быть бесконечно большим и, возможно, может быть непрерывным и, следовательно, несчетным (например, набор всех действительных чисел или всех действительных чисел в некотором ограниченном диапазоне). Набор возможных выходных значений может быть конечным или счетно бесконечным . Входные и выходные наборы, участвующие в квантовании, могут быть определены довольно общим образом. Например, векторное квантование - это приложение квантования к многомерным (векторным) входным данным.
Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (на графике — по вертикали). В АЦП округление может производиться до ближайшего меньшего уровня. Сигнал, к которому применены дискретизация и квантование, называется цифровым.
Квантование часто используется при обработке сигналов, в том числе при сжатии звука и изображений.
При оцифровке сигнала количество битов, кодирующих один уровень квантования, называют глубиной квантования или разрядностью. Чем больше глубина квантования и чем больше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае равномерного квантования глубина квантования определяет динамический диапазон, измеряемый в децибелах (1 бит на 6 дБ)
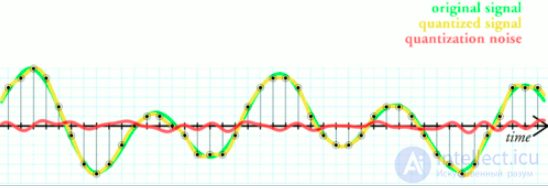

Квантованный сигнал
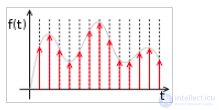
Неквантованный сигнал с дискретным временем
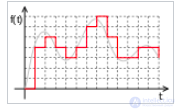
Цифровой сигнал
Равномерное (однородное) квантование — разбиение диапазона значений отсчетов сигнала на отрезки равной длины и замена этих значений на ближайший уровень квантования
. В этом случае возможны два варианта квантования
Неравномерное квантование — квантование, при котором разбиение диапазона значений сигнала производится на отрезки неравной длины. Применяется с целью повышения точности квантования в случае, когда распределение значений сигнала неравномерное, например при квантовании звука. При этом уровни квантования должны располагаться чаще в тех областях, где значения сигнала более вероятны. При квантовании речевых сигналов чаще используется компрессор, увеличивающий малые значения сигнала и уменьшающий большие значения, и последующее равномерное квантование.
Распространенное допущение для анализа ошибки квантования состоит в том, что она влияет на систему обработки сигнала аналогично тому, как аддитивный белый шум, имея пренебрежимо малую корреляцию с сигналом и приблизительно плоскую спектральную плотность мощности . Модель аддитивного шума обычно используется для анализа эффектов ошибок квантования в системах цифровой фильтрации и может быть очень полезной в таком анализе. Было показано, что это действительная модель в случаях квантования с высоким разрешением (малыеотносительно мощности сигнала) с гладкими функциями плотности вероятности.
Аддитивное шумовое поведение не всегда является верным предположением. Ошибка квантования (для квантователей, определенных как описано здесь) детерминированно связана с сигналом и не полностью от него независима. Таким образом, периодические сигналы могут создавать периодический шум квантования. А в некоторых случаях это может даже вызвать появление предельных циклов в системах цифровой обработки сигналов. Один из способов гарантировать эффективную независимость ошибки квантования от исходного сигнала - выполнить квантование с дизерингом (иногда с формированием шума ), которое включает добавление случайного (или псевдослучайного ) шума к сигналу перед квантованием. [14]
В типичном случае исходный сигнал намного больше, чем один младший значащий бит (LSB). В этом случае ошибка квантования существенно не коррелирует с сигналом и имеет приблизительно равномерное распределение . Когда округление используется для квантования, ошибка квантования имеет среднее значение, равное нулю, а значение среднеквадратичного значения (RMS) представляет собой стандартное отклонение этого распределения, определяемое выражением. Когда используется усечение, ошибка имеет ненулевое среднее значение
и среднеквадратичное значение
. В любом случае стандартное отклонение в процентах от полного диапазона сигнала изменяется с коэффициентом 2 для каждого 1-битного изменения числа битов квантования. Следовательно, потенциальное отношение мощности сигнала к мощности шума квантования изменяется на 4 или
, примерно 6 дБ на бит.
При более низких амплитудах ошибка квантования становится зависимой от входного сигнала, что приводит к искажению. Это искажение создается после сглаживания фильтра, и если эти искажения превышают 1/2 частоты дискретизации, они смещаются обратно в интересующую полосу. Чтобы сделать ошибку квантования независимой от входного сигнала, сигнал смешивается путем добавления шума к сигналу. Это немного снижает отношение сигнал / шум, но может полностью устранить искажения.
Шум квантования - это модель ошибки квантования, вносимой квантованием при аналого-цифровом преобразовании (АЦП). Это ошибка округления между аналоговым входным напряжением АЦП и выходным цифровым значением. Шум нелинейный и зависит от сигнала. Его можно смоделировать несколькими способами.
В идеальном аналого-цифровом преобразователе, где ошибка квантования равномерно распределена между -1/2 LSB и +1/2 LSB, а сигнал имеет равномерное распределение, охватывающее все уровни квантования, сигнал-шум квантования соотношение (SQNR) можно рассчитать из
где Q - количество бит квантования.
Наиболее распространенные тестовые сигналы, которые соответствуют этому, - это треугольные волны полной амплитуды и пилообразные волны .
Например, 16-битный АЦП имеет максимальное отношение сигнал / шум квантования 6,02 × 16 = 96,3 дБ.
Когда входной сигнал представляет собой синусоидальную волну полной амплитуды, распределение сигнала больше не является однородным, и вместо этого соответствующее уравнение выглядит следующим образом:
Здесь снова предполагается , что шум квантования распределен равномерно. Это так, когда входной сигнал имеет высокую амплитуду и широкий частотный спектр. [16] В этом случае 16-битный АЦП имеет максимальное отношение сигнал / шум 98,09 дБ. Разница в соотношении сигнал-шум 1,761 возникает только из-за того, что сигнал представляет собой полноразмерную синусоидальную волну, а не треугольник или пилообразную форму.
Для сложных сигналов в АЦП с высоким разрешением это точная модель. Для АЦП с низким разрешением, сигналов низкого уровня в АЦП с высоким разрешением и для простых сигналов шум квантования распределяется неравномерно, что делает эту модель неточной. [17] В этих случаях на распределение шума квантования сильно влияет точная амплитуда сигнала.
Расчеты относятся к входным данным на полномасштабном уровне. Для сигналов меньшего размера относительное искажение квантования может быть очень большим. Чтобы обойти эту проблему, можно использовать аналоговое компандирование , но это может привести к искажению.
Рис. 6.1.1 иллюстрирует типичный пример квантования скалярного сигнала. В процессе квантования значение отсчета аналогового сигнала сравнивается с набором пороговых уровней. Если отсчет попадает в интервал между двумя соседними пороговыми уровнями, то ему приписывается значение фиксированного уровня квантования, соответствующего данному интервалу. В цифровой системе каждому квантованному отсчету ставится в соответствие двоичная кодовая комбинация. В этом примере применен равномерный код, имеющий постоянную длину кодовых комбинаций.
Приступая к количественному анализу квантования скалярных величин, допустим, что 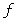 и
и 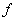 обозначают соответственно значения отсчета действительного скалярного сигнала до и после квантования. Предполагается, что
обозначают соответственно значения отсчета действительного скалярного сигнала до и после квантования. Предполагается, что 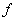 - случайная величина с плотностью вероятности
- случайная величина с плотностью вероятности 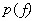 . Кроме того, предполагается, что
. Кроме того, предполагается, что 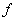 не выходит за пределы некоторого интервала:
не выходит за пределы некоторого интервала:
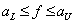 , (6.1.1)
, (6.1.1)
где 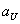 и
и 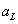 - верхняя и нижняя границы интервала.
- верхняя и нижняя границы интервала.
При решении задачи о квантовании необходимо выбрать такой набор пороговых уровней 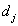 и уровней квантования
и уровней квантования 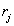 , что если
, что если
 , (6.1.2)
, (6.1.2)
то исходный отсчет заменяется на число, равное уровню квантования 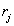 . На рис. 6.1.2, а приведен пример размещения пороговых уровней и уровней квантования на отрезке числовой оси, содержащем
. На рис. 6.1.2, а приведен пример размещения пороговых уровней и уровней квантования на отрезке числовой оси, содержащем 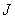 пороговых уровней. Другой распространенной формой представления характеристики квантователя является ступенчатая кривая (рис. 6.1.2, б).
пороговых уровней. Другой распространенной формой представления характеристики квантователя является ступенчатая кривая (рис. 6.1.2, б).
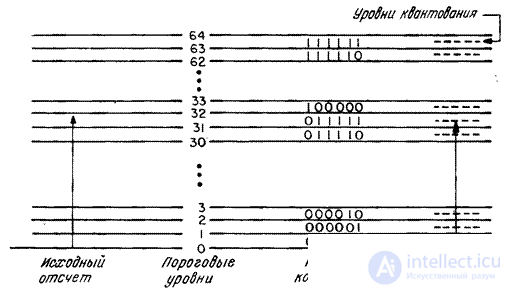
Рис. 6.1.1. Пример квантования сигнала.
Уровни квантования и пороговые уровни выбирают так, чтобы уменьшить до минимума некоторую заданную величину, характеризующую ошибку квантования, т. е. степень различия между 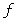 и
и 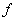 . В качестве меры ошибки квантования обычно выбирают среднеквадратическую ошибку. Если
. В качестве меры ошибки квантования обычно выбирают среднеквадратическую ошибку. Если 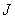 - число уровней квантования, то среднеквадратическая ошибка квантования равна
- число уровней квантования, то среднеквадратическая ошибка квантования равна
 . (6.1.3)
. (6.1.3)
Если число 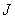 велико, то плотность вероятности значений квантуемого сигнала на каждом из интервалов
велико, то плотность вероятности значений квантуемого сигнала на каждом из интервалов 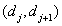 можно считать постоянной и равной
можно считать постоянной и равной 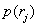 . Следовательно,
. Следовательно,
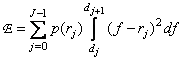 (6.1.4)
(6.1.4)
или после вычисления интегралов
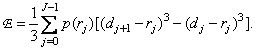 (6.1.5)
(6.1.5)
Оптимальное положение уровня квантования 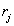 в интервале
в интервале 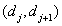 можно найти, решая задачу о минимуме ошибки
можно найти, решая задачу о минимуме ошибки 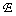 как функции
как функции 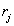 . Приравнивая нулю производную
. Приравнивая нулю производную
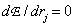 , (6.1.6)
, (6.1.6)
получаем
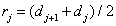 . (6.1.7)
. (6.1.7)
Таким образом, при сделанных допущениях оптимальным положением уровня квантования является середина интервала между соседними пороговыми уровнями.
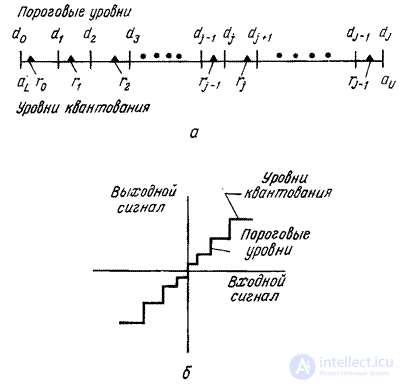
Рис. 6.1.2. Пороговые уровни и уровни квантования.
Подставив соответствующие величины в выражение для ошибки квантования, получим
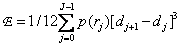 . (6.1.8)
. (6.1.8)
Оптимальное положение пороговых уровней можно определить, находя минимум ошибки 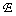 методом множителей Лагранжа. С помощью этого метода Пантер и Дайт показали, что положения пороговых уровней довольно точно определяются по формуле
методом множителей Лагранжа. С помощью этого метода Пантер и Дайт показали, что положения пороговых уровней довольно точно определяются по формуле
 (6.1.9a)
(6.1.9a)
где
 , (6.1.9б)
, (6.1.9б)
а 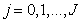 . Если плотность вероятности значений отсчетов равномерна, то пороговые уровни будут расставлены равномерно. При неравномерных плотностях пороговые уровни чаще в тех участках, где плотность вероятности велика, и реже там, где она мала. Для большинства видов плотности вероятности, используемых обычно при описании изображений, интегралы (6.1.9) взять не удается и положение пороговых уровней приходится находить с помощью численного интегрирования.
. Если плотность вероятности значений отсчетов равномерна, то пороговые уровни будут расставлены равномерно. При неравномерных плотностях пороговые уровни чаще в тех участках, где плотность вероятности велика, и реже там, где она мала. Для большинства видов плотности вероятности, используемых обычно при описании изображений, интегралы (6.1.9) взять не удается и положение пороговых уровней приходится находить с помощью численного интегрирования.
Если число уровней квантования невелико, то приближение, с помощью которого получено равенство (6.1.4), становится неоправданным и следует использовать точное выражение для ошибки (6.1.3). Дифференцируя его по переменным 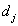 и
и 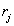 и приравнивая производные нулю, получаем
и приравнивая производные нулю, получаем
 , (6.1.10а)
, (6.1.10а)
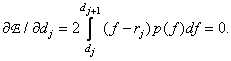 (6.1.10б)
(6.1.10б)
После преобразований приходим к системе уравнений
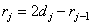 , (6.1.11а)
, (6.1.11а)
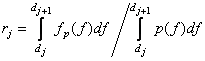 . (6.1.11б)
. (6.1.11б)
Решая эти уравнения рекуррентным способом, можно для заданной плотности вероятности 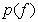 найти оптимальные значения пороговых уровней и уровней квантования. Макс решил такую задачу для гауссовой плотности и составил таблицы оптимального размещения пороговых уровней в зависимости от числа уровней квантования. В табл. 6.1.1 указано расположение уровней квантования и пороговых уровней в квантователе Макса для плотностей распределений вероятностей Гаусса, Лапласа, Рэлея и равномерного.
найти оптимальные значения пороговых уровней и уровней квантования. Макс решил такую задачу для гауссовой плотности и составил таблицы оптимального размещения пороговых уровней в зависимости от числа уровней квантования. В табл. 6.1.1 указано расположение уровней квантования и пороговых уровней в квантователе Макса для плотностей распределений вероятностей Гаусса, Лапласа, Рэлея и равномерного.
Таблица 6.1.1. Расположение уровней квантования и пороговых уровней в квантователе Макса
|
Число зарядов |
Равномерное |
Гаусса |
Лапласа |
Рэлея |
||||
|
1 |
-1,0000 |
-0,5000 |
-0,7979 |
-0,7071 |
0,0000 |
1,2657 |
||
|
|
0,0000 |
0,5000 |
0,0000 |
0,7979 |
0,0000 |
0,7071 |
2,0985 |
2,9313 |
|
|
1,0000 |
|
|
|
|
|||
|
2 |
-1,0000 |
-0,7500 |
-1,5104 |
-1,8340 |
0,0000 |
0,8079 |
||
|
|
-0,5000 |
-0,2500 |
-0,9816 |
-0,4528 |
-1,1269 |
-0,4198 |
1,2545 |
1,7010 |
|
|
-0,0000 |
0,2500 |
0,0000 |
0,4528 |
0,0000 |
0,4198 |
2,1667 |
2,6325 |
|
|
0,5000 |
0,7500 |
0,9816 |
1,5104 |
1,1269 |
1.8340 |
3,2465 |
3,8604 |
|
|
1,0000 |
|
|
|
|
|||
|
3 |
-1,0000 |
-0,8750 |
-2,1519 |
-3,0867 |
0,0000 |
0,5016 |
||
|
|
-0,7500 |
-0,6250 |
-1,7479 |
-1,3439 |
-2,3796 |
-1,6725 |
0,7619 |
1,0222 |
|
|
-0,5000 |
-0,3750 |
-1,0500 |
-0,7560 |
-1,2527 |
-0,8330 |
1,2594 |
1,4966 |
|
|
-0,2500 |
-0,1250 |
-0,5005 |
-0,2451 |
-0,5332 |
-0,2334 |
1,7327 |
1,9688 |
|
|
0,0000 |
0.1250 |
0,0000 |
0,2451 |
0,0000 |
0,2334 |
2,2182 |
2,4675 |
|
|
0,2500 |
0,3750 |
0,5005 |
0,7560 |
0,5332 |
0,8330 |
2,7476 |
3,0277 |
|
|
0,5000 |
0,6250 |
1,0500 |
1,3439 |
1,2527 |
1,6725 |
3,3707 |
3,7137 |
|
|
0,7500 |
0,8750 |
1,7479. |
2,1519 |
2,3796 |
3,0867 |
4,2124 |
4,7111 |
|
|
1,0000 |
|
|
|
|
|||
|
4 |
-1,0000 |
-0,9375 |
-2,7326 |
-4,4311 |
0,0000 |
0,3057 |
||
|
|
-0,8750 |
-0,8125 |
-2,4008 |
-2,0690 |
-3,7240 |
-3,0169 |
0,4606 |
0,6156 |
|
|
-0,7500 |
-0,6875 |
-1,8435 |
-1,6180 |
-2,5971 |
-2,1773 |
0,7509 |
0,8863 |
|
|
-0,6250 |
-0,5625 |
-1,4371 |
-1,2562 |
-1,8776 |
-1,5778 |
1,0130 |
1,1397 |
|
|
-0,5000 |
-0,4375 |
-1,0993 |
-0,9423 |
-1,3444 |
-1,1110 |
1,2624 |
1,3850 |
|
|
-0,3750 |
-0,3125 |
-0,7995 |
-0,6568 |
-0,9198 |
-0,7287 |
1,5064 |
1,6277 |
|
|
-0,2500 |
-0,1875 |
-0,5224 |
-0,3880 |
-0,5667 |
-0,4048 |
1,7499 |
1,8721 |
|
|
-0,1250 |
-0,0625 |
-0,2582 |
-0,1284 |
-0,2664 |
-0,1240 |
1,9970 |
2,1220 |
|
|
0,0000 |
0,0625 |
0,0000 |
0,1284 |
0,0000 |
0,1240 |
2,2517 |
2,3814 |
|
|
0,1250 |
0,1875 |
0,2582 |
0,3880 |
0,2644 |
0,4048 |
2,5182 |
2,6550 |
|
|
0,2500 |
0,3125 |
0,5224 |
0,6568 |
0,5667 |
0,7287 |
2,8021 |
2,9492 |
|
|
0,3750 |
0,4375 |
0,7995 |
0,9423 |
0,9198 |
1,1110 |
3,1110 |
3,2729 |
|
|
0,5000 |
0,5625 |
1,0993 |
3,2562 |
1,3444 |
1,5778 |
3,4566 |
3,6403 |
|
|
0,6250 |
0,6875 |
1.4371 |
1,6180 |
1,8776 |
2,1773 |
3,8588 |
4,0772 |
|
|
0,7500 |
0,8125 |
1,8435 |
2,0690 |
2,5971 |
3,0169 |
4,3579 |
4,6385 |
|
|
0,8750 |
0,9375 |
2,4008 |
2,7326 |
3,7240 |
4,4311 |
5,0649 |
5,4913 |
|
|
1,0000 |
|
|
|
|
|||
Нетрудно показать, что если пороговые уровни и уровни квантования выбраны согласно равенству (6.1.11), то среднеквадратическая ошибка квантования уменьшается до величины
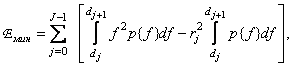 (6.1.12a)
(6.1.12a)
или в более короткой форме
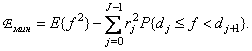 (6.1.12б)
(6.1.12б)
Для частного случая плотности равномерного распределения вероятностей минимальная среднеквадратическая ошибка равна
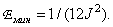 (6.1.13)
(6.1.13)
Для большинства других видов плотности вероятности ошибку квантования приходится определять с помощью расчетов.
Неравномерное квантование можно свести к равномерному с помощью нелинейного преобразования, как показано на рис. 6.1.3. Отсчет подвергается нелинейному преобразованию, зачтем равномерно квантуется и подвергается обратному нелинейному преобразованию . В системах квантования с преобразованием стремятся сделать плотность вероятности преобразованных отсчетов на входе квантователя равномерной. Преобразованный отсчет (рис. 6.1.3) есть
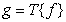 , (6.1.14)
, (6.1.14)
причем нелинейное преобразование 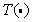 выбрано таким, что плотность вероятности
выбрано таким, что плотность вероятности 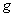 оказывается равномерной, т. е.
оказывается равномерной, т. е.
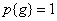 . (6.1.15)
. (6.1.15)
в интервале 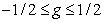 . Если
. Если 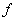 - случайная величина с нулевым средним, то искомая характеристика нелинейного элемента имеет вид
- случайная величина с нулевым средним, то искомая характеристика нелинейного элемента имеет вид
 . (6.1.16)
. (6.1.16)

Рис. 6.1.3. Квантователь со сжатием.
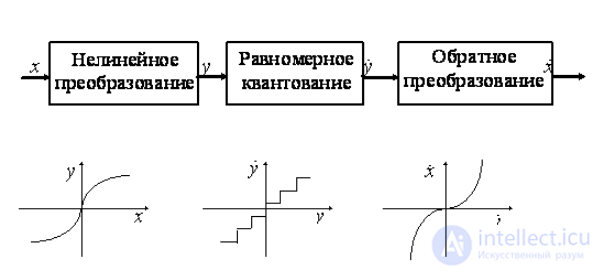
Рис.1.10. Квантование с предварительным нелинейным преобразованием
Таблица 6.1.2. Квантование с преобразованием
|
Плотность вероятности |
Прямое преобразование |
Обратное преобразование |
|
Гауссова Релея Лапласа
|
|
|
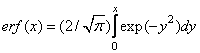 |
||
Таким образом, она совпадает с функцией распределения вероятностей величины . В табл. 6.1.2 приведены характеристики прямого и обратного нелинейных преобразований для плотностей распределений вероятностей Гаусса, Релея, Лапласа.
Надеюсь, эта статья об увлекательном мире квантование изображений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое квантование изображений, квантование скалярных величин и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Комментарии
Оставить комментарий
Цифровая обработка изображений
Термины: Цифровая обработка изображений