4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ

Привет, сегодня поговорим про процессы идеальной дискретизации, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое процессы идеальной дискретизации, восстановления непрерывных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

При разработке и анализе систем дискретизации и восстановления непрерывных изображений обрабатываемые изображения обычно принято рассматривать как детерминированные поля. Однако в некоторых случаях удобнее предполагать, что входной сигнал системы обработки изображений (особенно шумового происхождения) является реализацией двумерного случайного процесса. Ниже при анализе методов дискретизации и восстановления непрерывных изображений используются оба этих подхода.

4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ

Пусть функция 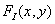 описывает исходное непрерывное изображение бесконечных размеров, представляя распределение яркости, оптической плотности или какого-либо другого параметра реального изображения. В идеальной системе дискретизации изображений пространственные отсчеты исходного изображения получаются фактически путем перемножения этой функции с пространственно-дискретизирующей функцией

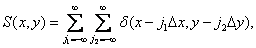     (4.1.1)

состоящей из бесконечного числа дельта-функций, заданных в узлах решетки с шагом 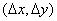, как показано на рис. 4.1.1. Тогда дискретизованное изображение описывается соотношением

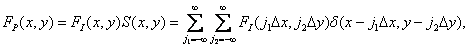     (4.1.2)

в котором учитывается, что функцию 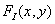 можно внести под знак суммирования и задать ее значения только в точках отсчета 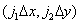. Для анализа процесса дискретизации удобно использовать спектр  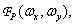получаемый в результате непрерывного двумерного преобразования Фурье дискретизованного изображения

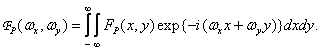     (4.1.3)

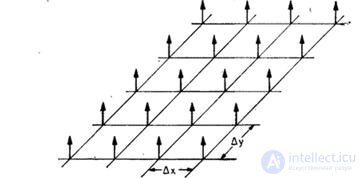
Рис. 4.1.1. Набор дельта-функций, осуществляющих дискретизацию изображений.

Согласно теореме о спектре свертки, спектр дискретизованного изображения можно представить в виде свертки спектра исходного изображения 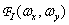 и спектра дискретизирующей функции 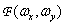, т. е.

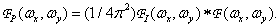     (4.1.4)

Двумерное преобразование Фурье дискретизирующей функции дает в результате бесконечный набор дельта-функций в плоскости пространственных частот с шагом 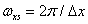 и 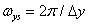 [4, стр. 22], т.е.

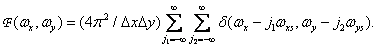     (4.1.5)

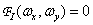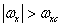Будем предполагать, что спектр исходного изображения ограничен по ширине так, что  при  и 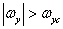. Вычисляя свертку согласно равенству (4.1.4), найдем

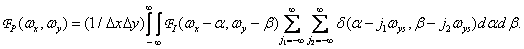     (4.1.6)

Меняя порядок операций суммирования и интегрирования и учитывая основное свойство дельта-функций, получаем выражение для спектра дискретизованного изображения

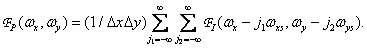     (4.1.7)

Как показано на рис. Об этом говорит сайт https://intellect.icu . 4.1.2, спектр дискретизованного изображения получается путем бесконечного повторения спектра исходного изображения со сдвигом на величины, кратные 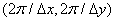. Следует отметить, что если  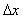и 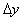 выбраны слишком большими по сравнению с шириной спектра 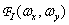, то соседние спектры будут перекрываться друг с другом.

Из отсчетов функции 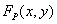 можно получить непрерывное изображение путем линейной пространственной интерполяции или с помощью линейной пространственной фильтрации дискретизованного изображения. Пусть  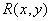есть импульсный отклик интерполирующего фильтра, а  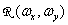- его частотная характеристика. Восстановленное изображение получается как свертка последовательности отсчетов с импульсным откликом восстанавливающего фильтра. Таким образом, восстановленное непрерывное изображение описывается соотношением

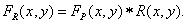   (4.1.8)

Подставляя 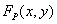 из равенства (4.1.2) и вычисляя свертку, получаем

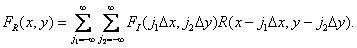     (4.1.9)

Отсюда видно, что импульсный отклик 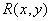 выполняет роль двумерной функции, интерполирующей отсчеты на всю плоскость. Пространственно-частотный спектр изображения, восстановленного согласно равенству (4.1.8), есть произведение частотной характеристики восстанавливающего фильтра со спектром дискретизованного изображения, т. е.

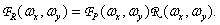                                                                    (4.1.10)

С учетом равенства (4.1.7) получаем

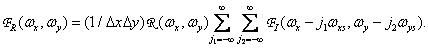     (4.1.11)

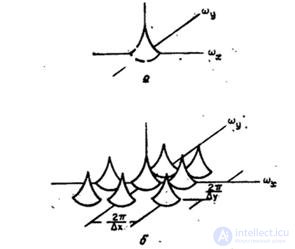
Рис. 4.1.2. Типичный спектр дискретизованного изображения: а - исходное изображение; б - дискретизованное изображение.

Из этого выражения видно, что если спектры не перекрываются, а множитель 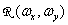 подавляет все сдвинутые спектры при 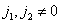, то спектр восстановленного непрерывного изображения будет совпадать со спектром исходного изображения и поэтому изображения также будут одинаковыми. Для изображений с ограниченной шириной спектра первое условие выполняется, если интервал дискретизации выбран так, что прямоугольная область, ограниченная верхними граничными частотами спектра изображения 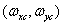, лежит внутри прямоугольной области, определяемой половинами частот дискретизации 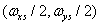. Следовательно, должны выполняться неравенства

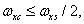
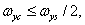     (4.1.12а)

или

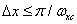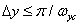,  .   (4.1.12б)

Это означает, что шаг дискретизации не должен превышать половины периода пространственной гармоники, соответствующей самым мелким деталям изображения. Это условие эквивалентно теореме о дискретизации одномерных сигналов, в которой сформулировано требование, что частота дискретизации должна хотя бы вдвое превышать наивысшую частоту спектра сигнала. Если соотношения (4.1.12) выполняются со знаками равенства, то изображение дискретизуется с найквистовской (в отечественной литературе это положение известно как теорема Котельникова) частотой; есл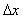и  и 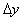 меньше или больше, чем требуется по критерию Найквиста, то говорят, что изображение дискретизуется с избыточной или недостаточной частотой.

В тех случаях, когда пространственная частота дискретизации изображения достаточна для устранения наложения спектров в дискретизованном изображении, исходное изображение можно абсолютно точно восстановить путем пространственной фильтрации отсчетов с помощью соответствующего фильтра. Так, например, фильтр, частотная характеристика которого приведена на рис. 4.1.3 и описывается выражениями

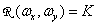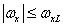 при  и 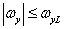                    (4.1.13а)

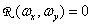 в остальных случаях,                  (4.1.13б)

где 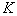 - масштабная постоянная, удовлетворяет условию точного восстановления, есл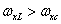и  и 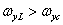. Функция рассеяния точки (или импульсный отклик) данного восстанавливающего фильтра имеет вид

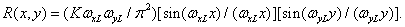     (4.1.14)

При использовании этого фильтра изображение восстанавливается с помощью бесконечной суммы функций вида 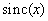. Другим фильтром, пригодным для восстановления изображений, является «круговой» фильтр с частотной характеристикой (рис. 4.1.3, б)

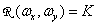 при 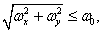     (4.1.15а)

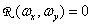 в остальных случаях,     4.1.15б)

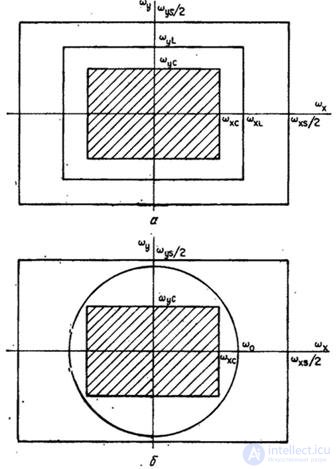
Рис. 4.1.3. Фильтры для восстановления дискретизованных изображений: а - прямоугольный; б - круговой.

если 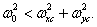 Импульсный отклик такого фильтра имеет вид                                           

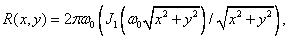     (4.1.16)

где 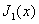 - бесселева функция первого порядка. Существует много восстанавливающих фильтров (или соответствующих интерполяционных функций), которые можно использовать для восстановления изображений. Однако на практике в цифровой системе воспроизведения изображений часто бывает сложно реализовать оптимальный восстанавливающий фильтр. Одна из практических трудностей состоит в том, что обычные интерполяционные функции [например, заданные равенствами (4.1.14) и (4.1.16)] принимают не только положительные, но и отрицательные значения, хотя функции, описывающие восстановленные изображения, строго положительны. Такие интерполяционные функции нельзя сформировать оптическими средствами и, следовательно, не удается восстановить изображения путем последовательного их взвешивания и сложения. Ричардс [6] нашел семейство интерполяционных функций, которые можно применить для последовательной оптической интерполяции, поскольку их большие значения положительны.

Надеюсь, эта статья об увлекательном мире процессы идеальной дискретизации, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое процессы идеальной дискретизации, восстановления непрерывных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений