5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ

Привет, сегодня поговорим про сингулярное разложение матрицы, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сингулярное разложение матрицы , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Известно, что любую матрицу 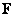 размера 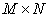, имеющую ранг 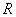, можно представить в виде взвешенной суммы матриц единичного ранга размера 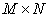. Такое представление называется сингулярным разложением [6-8]. В последующих разделах будет рассмотрено применение этого метода для обработки изображений.

При сингулярном разложении используют унитарную матрицу 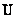 размера  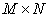и унитарную матрицу  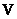размера 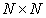, такие, что

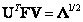,                                     (5.2.1)

где матрица

              (5.2.2)

имеет размеры 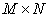, а ее диагональные элементы  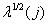называются сингулярными значениями матрицы 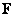. Об этом говорит сайт https://intellect.icu . Поскольку матрицы  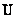и 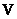 унитарны, то  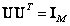и . Поэтому

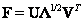.                                     (5.2.3)

Столбцы унитарной матрицы 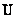 являются собственными векторами  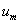симметричной матрицы 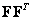, т. е.

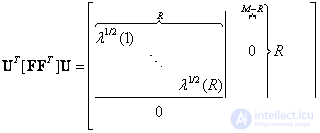  (5.2.4)

где 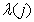 - ненулевые собственные значения матрицы 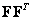. Аналогично строки матрицы  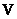являются собственными векторами  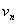симметричной матрицы , т. е.

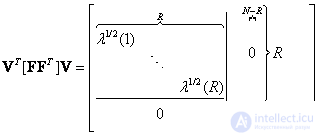   (5.2.5)

где 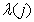 - соответствующие ненулевые собственные значения матрицы . Нетрудно проверить, что равенство (5.2.3) согласуется с (5.2.4) и (5.2.5).

Разложение матрицы 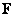, задаваемое соотношением (5.2.3), можно представить в виде ряда

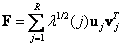.                           (5.2.6)

Матричные произведения собственных векторов 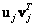 образуют набор матриц единичного ранга, каждая из которых умножается на весовой множитель, являющийся соответствующим сингулярным значением матрицы 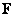. Согласованность разложения (5.2.6) с вышеприведенными соотношениями можно показать, подставив его в равенство (5.2.1). В результате получается

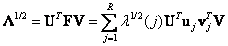.     (5.2.7)

Заметим, что произведение 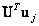, дает вектор-столбец, 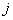-й элемент которого равен единице, а все остальные - нули. Вектор-строка, получающаяся в результате вычисления произведения  , имеет аналогичный вид. Поэтому в правой части равенства (5.2.7) образуется диагональная матрица, элементы которой равны сингулярным значениям матрицы .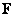

Матричное разложение (5.2.3) и эквивалентное представление в виде ряда (5.2.6) можно найти для любой матрицы. Поэтому такое разложение можно непосредственно применить для обработки дискретных изображений, представленных в виде матриц. Кроме того, этими формулами можно воспользоваться для разложения матриц линейных преобразований изображений. Применение метода сингулярного разложения для исправления и кодирования изображений рассмотрено в последующих главах книги.

Надеюсь, эта статья об увлекательном мире сингулярное разложение матрицы, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое сингулярное разложение матрицы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений