4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ

Привет, сегодня поговорим про влияние неидеальности восстанавливающих фильтров, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое влияние неидеальности восстанавливающих фильтров , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Проанализируем теперь работу реальных систем восстановления непрерывных изображений. Будем предполагать, что входной сигнал такой системы состоит из отсчетов некоторого исходного изображения, полученных на найквистовской частоте с помощью конечного набора дельта-функций. Согласно равенству (4.1.9), восстановленное изображение описывается функцией

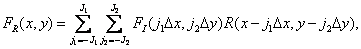     (4.3.3)

где 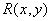 - двумерная интерполяционная функция. В идеальном случае восстановленное изображение должно быть точной копией исходного, т. е.

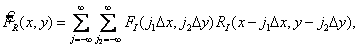     (4.3.4)

где 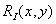 обозначает оптимальную интерполяционную функцию, например заданную формулой (4.1.14) или (4.1.16). В этом случае ошибка восстановления для произвольной точки изображения равна

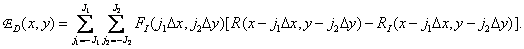     (4.3.5)

Величина ошибки восстановления зависит от двух факторов: а) в реальной системе интерполяционная функция 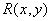 может отличаться от идеальной интерполяционной функции 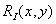, б) восстановленное изображение имеет конечные размеры и поэтому интерполяционные функции отсекаются на его границах. В большинстве систем, оперирующих с дискретизованными изображениями, ошибками восстановления вблизи границ обычно пренебрегают, так как они становятся весьма малыми при удалении от границ изображения на несколько шагов дискретизации. Неидеальность интерполяционных функций в принципе приводит к ухудшению резкости изображения, а также к появлению паразитных высокочастотных составляющих.

Влияние неидеальности восстанавливающего фильтра удобно исследовать, рассматривая структуру спектра восстановленного изображения, определяемого соотношением (4.1.11):

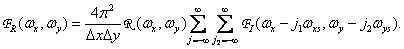     (4.3.6)

В идеальном случае множитель 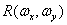 должен выделять составляющие спектра нулевого порядка при 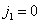, , 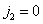а все остальные составляющие должны подавляться. Об этом говорит сайт https://intellect.icu . В неидеальном фильтре могут ослабляться составляющие спектра нулевого порядка, что приводит к ухудшению резкости, и, кроме того, гармоники спектров более высокого порядка могут подавляться не полностью, что искажает восстановленное изображение. На рис. 4.3.7 приведен пример, показывающий характер искажений спектра изображения при использовании неидеального восстанавливающего фильтра. Типичное сечение спектра дискретизованного изображения представлено на рис. 4.3.7, а. При использовании идеального восстанавливающего фильтра, когда интерполяционные функции имеют вид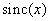, составляющие спектра нулевого порядка выделяются, а все составляющие побочных спектров полностью подавляются (рис. 4.3.7, в). На рис. 4.3.7, г показана частотная характеристика восстанавливающего фильтра, основанного на интерполяционной функции нулевого порядка, когда значения восстановленных элементов в окрестности точки отсчета устанавливаются равными значению в точке отсчета. В результате получается спектр (рис. 4.3.7, д), искаженный за счет ослабления некоторых составляющих спектра нулевого порядка и появления ложных высокочастотных составляющих.

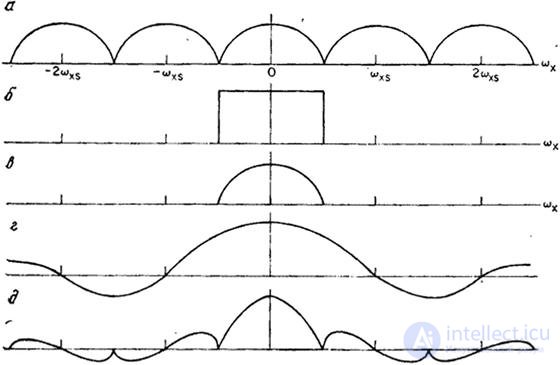
Рис. 4.3.7. Энергетические спектры при идеальном и неидеальном восстановлении: а - спектр дискретизованного изображения; б - частотная характеристика идеального восстанавливающего фильтра; в - спектр изображения после идеального восстановления; г - частотная характеристика восстанавливающего фильтра с интерполяцией нулевого порядка; д - спектр изображения, восстановленного с интерполяцией нулевого порядка.

Повторяя шаги, сделанные при выводе равенства (4.2.21), получим, что потери резкости, вызванные неидеальностью восстанавливающей функции 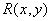, количественно можно выразить с помощью отношения

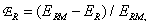                                                            (4.3.7)

где интеграл

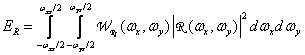     (4.3.8)

представляет собой энергию тех составляющих неидеально восстановленного изображения, которые лежат в найквистовском диапазоне, а интеграл

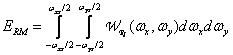                                (4.3.9)

описывает энергию таких составляющих идеально восстановленного изображения.

Ошибку восстановления, связанную с внесением ложных высокочастотных составляющих спектра, можно определить отношением

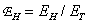     (4.3.10)

где

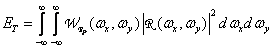                   (4.3.11)

есть полная энергия восстановленного изображения, а

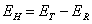                                                                               (4.3.12)

представляет собой энергию всех спектральных составляющих восстановленного изображения, лежащих вне найквистовского диапазона.

В табл. 4.3.2 приведены значения ошибки восстановления 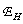 и коэффициента потери резкости  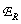полученные при восстановлении с использованием некоторых двумерных разделимых интерполяционных функций.

Таблица 4.3.2. Ошибка восстановления и коэффициент потери резкости для различных разделимых двумерных интерполяционных функций

Здесь предполагалось, что спектральная плотность исходного изображения описывается формулами

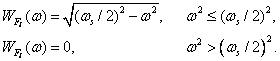        (4.3.13)

Кроме того, предполагалось, что вклад, вносимый в ошибку восстановления побочных спектров при 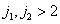, пренебрежимо мал. Из таблицы видно, что при восстановлении с использованием прямоугольных интерполяционных функций (функций нулевого порядка) коэффициент потери резкости и ошибка восстановления получаются довольно большими. Применяя интерполяционные функции более высокого порядка, ошибку восстановления можно значительно уменьшить, но за счет дальнейшего ухудшения коэффициента потери резкости

Надеюсь, эта статья об увлекательном мире влияние неидеальности восстанавливающих фильтров, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое влияние неидеальности восстанавливающих фильтров и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений