10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ

Привет, Вы узнаете о том , что такое сингулярное преобразование, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сингулярное преобразование , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

сингулярное преобразование [34] является двумерным унитарным преобразованием, основанным на сингулярном разложении матриц (см. гл. 5). Прямое сингулярное преобразование по определению равно

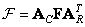,             (10.9.1)

а обратное преобразование

.             (10.9.2)

Матрица преобразования строк 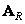 обеспечивает выполнение операции диагонализации

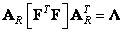,               (10.9.3)

где 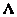 - диагональная матрица, элементы  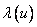которой являются собственными значениями матрицы . Аналогично

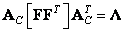.               (10.9.4)

Подставив выражение (10.9.2) в равенства (10.9.3) и (10.9.4), получим

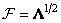,                   (10.9.5)

где элементами диагональной матрицы 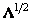 являются числа 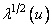, называемые сингулярными значениями матрицы  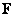и равные квадратному корню из соответствующих собственных значений .

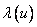Матрицу изображения можно записать в очень компактной форме с помощью матричного произведения векторов, получаемых при сингулярном разложении. Об этом говорит сайт https://intellect.icu . Согласно равенству (10.1.14б),

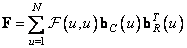,                       (10.9.6)

где 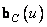 и  представляют собой векторы, состоящие из элементов 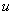-х столбцов матриц  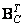и .

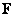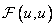Пользуясь сингулярным преобразованием, матрицу изображения , содержащую  элементов, можно полностью описать  величинами, представляющими, собой  коэффициентов . Однако следует отметить, что конкретные значения элементов матриц преобразований по строкам и столбцам в этом случае зависят от элементов изображения.

На рис. 10.9.1 приведен пример сингулярного преобразования изображения. Здесь же показаны произведения 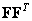 и , а также соответствующие матрицы преобразований по строкам  и по столбцам 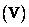. Сингулярные значения рассматриваемого изображения представлены на рис. 10.9.2. На рис. 10.9.3 показано несколько матричных произведений .

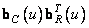Рис. 10.9.1. Сингулярное преобразование изображения «Портрет». Все представленные массивы из 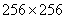 элементов получены из массивов размера  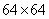элемента посредством билинейной интерполяции.

а - исходное изображение, матрица 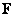; б - результат сингулярного преобразования, матрица 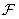; в - матрица 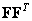; г - матрица ; д - матрица, состоящая из модулей элементов матрицы ; е - матрица, состоящая из модулей элементов матрицы .

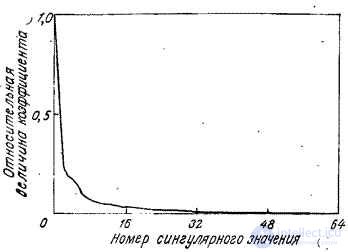
Рис. 10.9.2. Сингулярные значения изображения «Портрет».

Рис. 10.9.3. Базисные изображения для изображения «Портрет».

Рисунки а, б, в, г, д, е соответствуют , , , , , .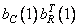

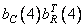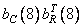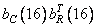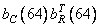Выводы из данной статьи про сингулярное преобразование указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое сингулярное преобразование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений