Лекция
Привет, Вы узнаете о том , что такое сравнение различных преобразований, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сравнение различных преобразований , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
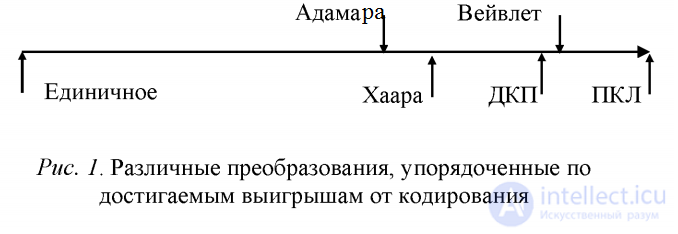
Преобразование Адамара основано на квадратной матрице Адамара , элементы которой равны плюс или минус единице, а строки и столбцы образуют ортогональные векторы . Нормированная матрица Адамара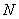 
-го порядка удовлетворяет соотношению 
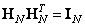. Среди ортонормальных матриц Адамара наименьшей является матрица второго порядка 
.
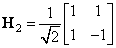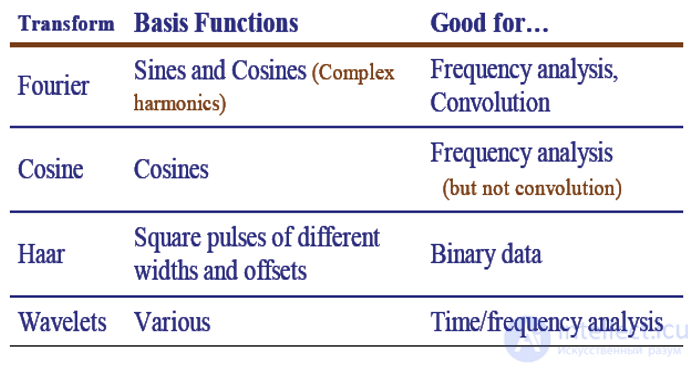
Вейвлет-преобразование (англ. Wavelet transform) — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом. Об этом говорит сайт https://intellect.icu . Вейвлет-преобразование переводит сигнал из временного представления в частотно-временное. Способ преобразования функции (или сигнала) в форму, которая или делает некоторые величины исходного сигнала более поддающимися изучению, или позволяет сжать исходный набор данных. Вейвлетное преобразование сигналов является обобщением спектрального анализа. Термин (англ. wavelet) в переводе с английского означает «маленькая волна». Вейвлеты — это обобщенное название математических функций определенной формы, которые локальны во времени и по частоте и в которых все функции получаются из одной базовой, изменяя ее (сдвигая, растягивая).
Вейвлет Хаара — один из первых и наиболее простых вейвлетов. Он основан на ортогональной системе функций, предложенной венгерским математиком Альфредом Хааром в 1909 году. Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими. Впоследствии Ингрид Добеши стала развивать теорию ортогональных вейвлетов и предложила использовать функции, вычисляемые итерационным путем, названные вейвлетами Добеши.Без ущерба для качества сжимает размер файла изображения с длинными участками одинаковых значений яркости - Сохраняет основные черты изображения, понижая его разрешение и существенно сокращая данные при отбросе детализирующих матриц.
Дискретное косинусное преобразование (англ. Discrete Cosine Transform, DCT) — одно из ортогональных преобразований. Вариант косинусного преобразования для вектора действительных чисел. Применяется в алгоритмах сжатия информации с потерями, например, MPEG и JPEG. Это преобразование тесно связано с дискретным преобразованием Фурье и является гомоморфизмом его векторного пространства. Математически преобразование можно осуществить умножением вектора на матрицу преобразования. При этом матрица обратного преобразования с точностью до множителя равна транспонированной матрице. В математике матрицы выбирают так, чтобы преобразование было ортонормированным, а постоянный множитель равен единице. В компьютерных приложениях это не всегда так. Различные периодические продолжения сигнала ведут к различным типам ДКП.
Преобразование Карунена-Лоэва (ПКЛ). Метод преобразования непрерывных сигналов в набор некоррелированных коэффициентов разработан Каруненом и Лоэвом . Как указывается в статье [30], Хотеллинг [29] первым предложил метод преобразования дискретных сигналов в набор некоррелированных коэффициентов. Однако в большинстве работ по цифровой обработке сигналов и дискретное, и непрерывное преобразования называют преобразованием Карунена-Лоэва или разложением по собственным векторам.
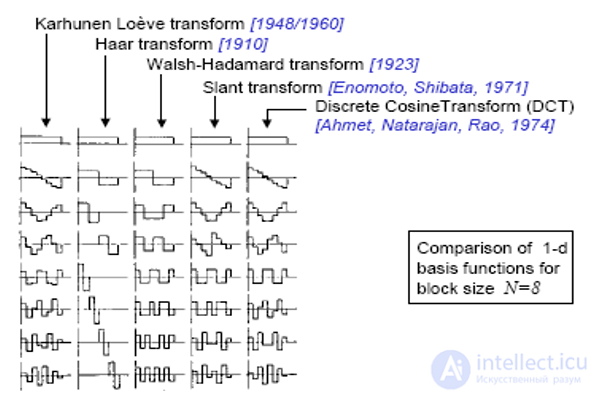
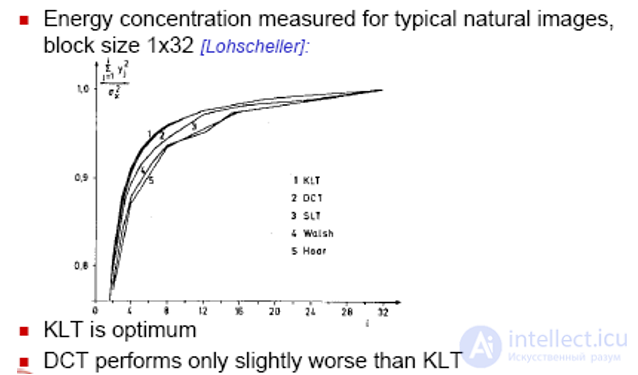
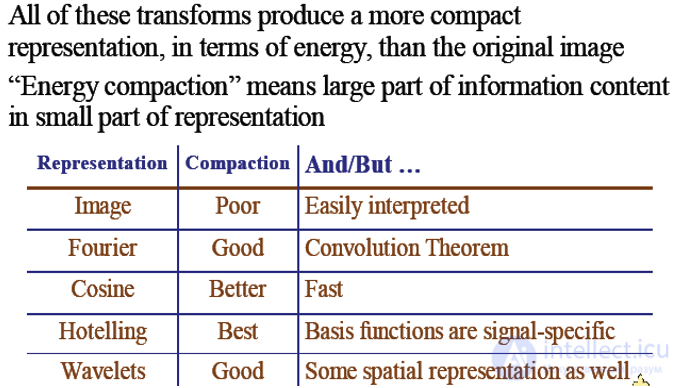
Все эти преобразования дают более компактное представление с точки зрения энергии, чем исходное изображение.
«Энергетическое сжатие» означает большую часть информационного содержания в небольшой части представления.
| Представление | уплотнения | и / но ... |
| изображение | Плохое | Легко интерпретируется |
| Фурье | хорошей | теорема о свертке |
| Косинус | лучше | быстро |
| Hotelling | Best | Basis Функции зависят от сигнала |
| Вейвлеты | Хорошо | Некоторое пространственное представление |
Исследование, описанное в статье про сравнение различных преобразований, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое сравнение различных преобразований и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про сравнение различных преобразований
Комментарии