4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА

Привет, сегодня поговорим про влияние формы дискретизирующего импульса, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое влияние формы дискретизирующего импульса , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

С учетом вышеупомянутых предположений дискретизованное изображение можно описать функцией

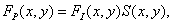                                    (4.2.1)

где дискретизирующая функция

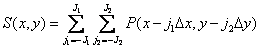     (4.2.2)

состоит из  одинаковых импульсов 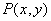, образующих решетку с шагом 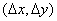. Для упрощения обозначений пределы суммирования выбраны симметричными. Будем считать, что дискретизирующие импульсы нормированы так, что

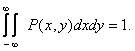                                                 (4.2.3)

При анализе можно полагать, что дискретизирующая функция была получена пропусканием конечного наборадельта-функций 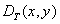 через линейный фильтр с импульсным откликом 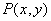. Таким образом,

                                 (4.2.4)

где

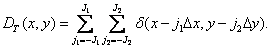     (4.2.5)

Подставив выражение (4.2.2) в (4.2.1), получим формулу для дискретизованного изображения

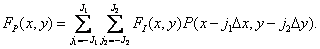     (4.2.6)

Спектр этой функции имеет вид

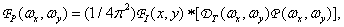     (4.2.7)

где 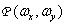 - результат преобразования Фурье функции 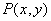. Преобразование Фурье конечной решетки дискретизирующих импульсов описывается следующим соотношением [5, стр. Об этом говорит сайт https://intellect.icu . 105]:

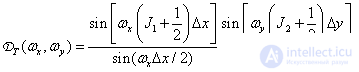      (4.2.8)

На рис. 4.2.2 приведен график функции 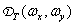. С увеличением  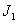и 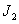 правая часть формулы (4.2.8) в пределе превращается в набор дельта-функций.

В системе восстановления изображений непрерывное изображение получается путем интерполяции отсчетов. Идеальные интерполяционные функции, такие, как 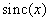 и бесселевы [формулы (4.1.14) и (4.1.16)], обычно определены на бесконечной плоскости. Если же дискретизирующая решетка имеет конечные размеры, то на границах отсекаются «хвосты» интерполяционных функций и вблизи краев восстановленного изображения появляются ошибки [9, 10]. Однако такие ошибки обычно становятся пренебрежимо малыми при удалении от границ на 8-10 шагов дискретизации.

Числовые значения отсчетов изображения получаются путем пространственного интегрирования 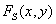 по некоторой конечной площадке - элементу изображения. В сканирующей системе

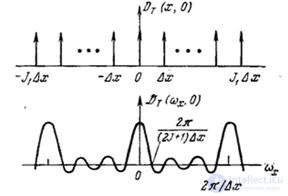
Рис. 4.2.2. Усеченная дискретизирующая последовательность и ее спектр.

(рис. 4.2.1) интегрирование фактически проводится на светочувствительной поверхности фотодетектора. Значение отсчета, соответствующего 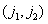-му элементу, можно найти по формуле

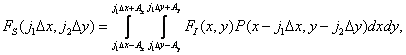     (4.2.9)

где 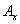 и 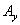 обозначают наибольшие размеры этого элемента. Здесь предполагается, что за время интегрирования в системе берется лишь один отсчет. В противном случае приходится решать сложную проблему перекрестных искажений. В рассматриваемой системе дискретизации размеры элемента могут оказаться больше, чем расстояние между отсчетами. Поэтому в модели допускается, что последовательные (во времени) отсчеты соответствуют частично перекрывающимся элементам изображения.

Простой заменой переменных равенство (4.2.9) можно преобразовать к виду

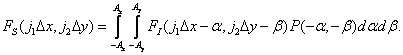     (4.2.10)

Поскольку предполагается, что за время интегрирования берется только один отсчет, пределы в интеграле (4.2.10) можно расширить до бесконечности. В такой форме выражение (4.2.10) можно рассматривать как результат сверткиисходного изображения 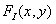 с импульсным откликом  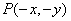и последующей дискретизации этой свертки в конечной области с помощью дельта-функций. Тогда, пренебрегая эффектами, связанными с конечными размерами дискретизирующей решетки дельта-функций, получим

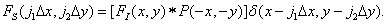     (4.2.11)

В большинстве систем дискретизации дискретизирующий импульс симметричен, поэтому .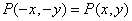

Несложное по форме соотношение (4.2.11) полезно при оценке эффектов, возникающих при дискретизации с использованием импульсов конечной ширины. Если спектр изображения ограничен по ширине, а 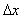 и  удовлетворяют критерию Найквиста, то конечная ширина импульса приводит к тем же результатам, как если бы исходное изображение перед идеальной дискретизацией подверглось линейному искажению (смазыванию). В части 4 будут рассмотрены методы компенсации подобных искажений. Однако конечность размеров дискретизирующего импульса не всегда является недостатком. Рассмотрим случай, когда спектр исходного изображения очень широкий, и поэтому оно дискретизируется с недостаточной частотой. Импульс с конечными размерами фактически осуществляет низкочастотную фильтрацию исходного изображения, что приводит к сужению спектра и, следовательно, уменьшает ошибки, вызванные наложением спектров.

Надеюсь, эта статья об увлекательном мире влияние формы дискретизирующего импульса, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое влияние формы дискретизирующего импульса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений