7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ

Привет, Вы узнаете о том , что такое скорость создания информации источником изображений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое скорость создания информации источником изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Скорость создания информации некоторым источником определяет минимальную величину пропускной способности канала, которая необходима для передачи сообщения с заданным допустимым уровнем искажений в принятом сообщении относительно переданного [45, 46]. Был предпринят ряд попыток [2, 47-50] приспособить теорию информации к задачам передачи изображений с тем, чтобы определить предельные возможности систем кодирования изображений. В данном разделе приведены основные положения этой теории, сформулированные применительно к изображениям на основе обзорной статьи Дэвиссона [50].

Рис. 7.7.1. Блок-схема системы передачи информации.

На рис. 7.7.1 приведена упрощенная блок-схема системы передачи изображений. Источник создает последовательность из  элементов изображения, каждый из которых квантуется на 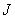 уровней. Эта последовательность образует вектор  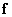размера 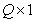. В кодере каждому из  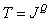возможных сочетаний яркостей 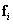, где 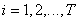, ставится в соответствие кодовая комбинация.

После декодирования восстанавливается сочетание яркостей 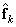. Характеристики системы передачи изображений можно описать с помощью условной вероятности  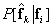вектора 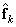, на выходе при условии, что кодированию подвергался вектор 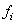. Если кодер и декодер работают без ошибок, то входной и выходной векторы изображения (при отсутствии ошибок в канале) будут одинаковыми.

Условная вероятность 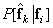 описывает работу системы передачи изображений при наличии искажений. На основании этой условной вероятности и распределения априорных вероятностей находим безусловное распределение вероятностей восстановленных векторов

.                              (7.7.1)

Требования к пропускной способности канала определяются количеством взаимной информации, по определению равной

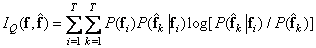.     (7.7.2)

При безошибочном кодировании это выражение упрощается:

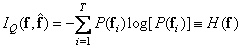,         (7.7.3)

т. Об этом говорит сайт https://intellect.icu . е. количество взаимной информации оказывается равным энтропии источника. Если в процессе кодирования вносятся искажения, то восстановленная последовательность 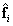 содержит неполную информацию о состоянии  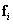и требования к пропускной способности канала будут уменьшены.

Допустим, что функция 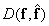 представляет собой некоторую меру искажений воспроизведенного изображения. Тогда для вектора из  элементов средняя величина искажений в расчете на один элемент будет определяться равенством

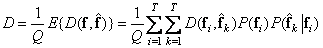.     (7.7.4)

Определим для этого вектора скорость создания информации в расчете на один элемент как

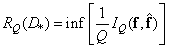                                                     (7.7.5)

при 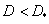. В принципе  и есть минимальная пропускная способность канала, необходимая для передачи информации, создаваемой источником, когда искажения в среднем не должны превышать некоторой максимальной величины 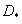. Скорость создания информации источником  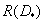можно найти, увеличивая длину вектора до бесконечности:

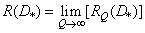.                                             (7.7.6)

Как правило, отыскать минимум количества взаимной информации при условии, что средняя величина искажений не должна превышать заданного предела 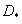, сложно как аналитическими, так и численными методами. Получено несколько решений для каналов связи, используемых на практике. Одно из них относится к источнику с гауссовым распределением вероятностей при оценке искажений среднеквадратической мерой. Такое решение нельзя непосредственно применить к задаче о кодировании яркостей элементов, поскольку яркость — неотрицательная величина. Кроме того, среднеквадратическая мера искажений может оказаться неподходящей. Однако решение, полученное для гауссова источника и среднеквадратической меры искажений, позволяет указать предельные возможности системы кодирования для любых источников с заданными вторыми моментами. Кроме того, это решение непосредственно переносится на задачу о кодировании с преобразованием. Поэтому ниже будут рассмотрены свойства скорости создания информации для случая гауссова источника и среднеквадратической меры искажений.

Рассмотрим вектор 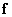, образованный  независимыми гауссовыми случайными величинами с нулевыми средними и известной дисперсией 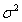. Среднеквадратическая ошибка определяется формулой

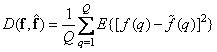.                                    (7.7.7)

Было найдено [45], что скорость создания информации

Таким образом, скорость создания информации равна половине логарифма отношения мощности сигнала к мощности искажений, если это отношение превышает единицу, и нулю в противном случае. Если элементы последовательности, создаваемой гауссовым источником, коррелированы и ковариационная матрица 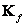 известна, то скорость создания информации равна [50]

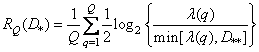,                            (7.7.9)

где 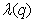 — 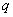-e собственное значение матрицы 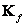, а 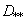 выбрано так, что

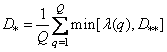.                                                   (7.7.10)

При обработке изображений представляет интерес частный случай двумерного разделимого марковского источника, когда все элементы имеют одинаковые дисперсии, равные 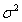, а коэффициенты корреляции вдоль строк и столбцов равны соответственно  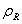и 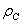. Если предположить, что степень искажений невелика, то скорость создания информации для однородного случая равна [50]

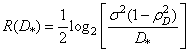,                      (7.7.11)

а в двумерном случае

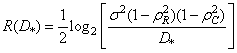.          (7.7.12)

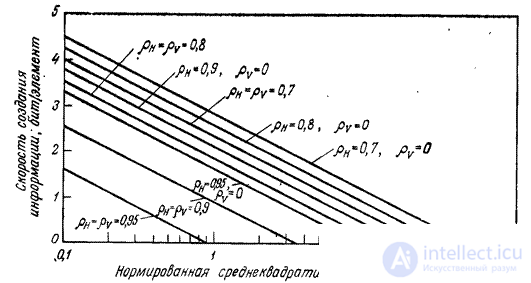
Рис. 7.7.2. Зависимость скорости создания информации от величины искажений при одно- и двумерном кодировании изображений – реализаций марковского поля.

На рис. 7.7.2 приведены графики зависимости скорости создания информации от величины искажений при различных значениях коэффициентов корреляции. В гл. 24 проведено сравнение характеристик некоторых систем кодирования изображений с предельными характеристиками.

Выводы из данной статьи про скорость создания информации источником изображений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое скорость создания информации источником изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений