8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Привет, Вы узнаете о том , что такое решение систем линейных уравнений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое решение систем линейных уравнений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Систему линейных уравнений

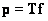                                               (8.4.1)

где 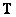 - матрица размера 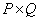, можно рассматривать как систему из  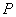уравнений с  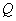неизвестными. Возможны три случая:

1. Система уравнений имеет единственное решение 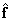, для которого .

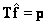2. Системе уравнений удовлетворяют несколько решений.

3. Система уравнений не имеет точного решения.

Если система уравнений имеет хотя бы одно решение, то ее называют совместной, а в противном случае - несовместной. Системы уравнений, не имеющие решений, часто получаются при исследовании физических систем, когда вектор 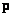 описывает последовательность измерений наблюдаемых величин, которые по предположению являются следствием воздействия некоторой недоступной для прямого наблюдения движущей силы, представленной вектором 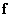. Об этом говорит сайт https://intellect.icu . Матрица  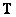получается посредством математического моделирования характеристик реальной системы, для которой вектор  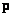является выходным сигналом. При исправлении (реставрации) изображений вектор  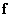обычно представляет исходное изображение, вектор  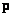- смазанное изображение, а матрица  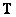описывает дискретную математическую модель процесса, приводящего к смазыванию изображения. Поскольку матрица  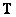и вектор  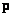обычно определяются с некоторой погрешностью, может оказаться, что этот вектор не соответствует ни одному из возможных векторов воздействия .

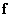Рассмотрим теперь вопрос о существовании решений системы уравнений 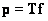. Из структуры системы уравнений видно, что решение будет существовать тогда и только тогда, когда вектор  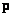может быть получен линейной комбинацией столбцов матрицы 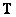. В этом случае говорят, что вектор  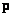лежит в пространстве столбцов матрицы 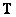. Более строгой формулировкой условия существования решения является следующая [4]: система уравнений  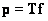имеет решение тогда и только тогда, когда для матрицы  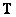существует условно обратная матрица 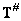, удовлетворяющая уравнению .

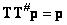Значит, для существования решения необходимо, чтобы при отображении из пространства наблюдаемых изображений в пространство исходных изображений (с помощью условно обратной матрицы 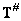) и обратно (с помощью матрицы 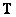) снова получался вектор наблюдаемых величин 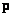. Если система уравнений является недоопределенной (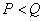), то решение существует тогда, когда ранг матрицы  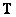равен 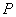, т. е. полному числу строк. Во всех остальных случаях, в том числе и для переопределенной системы уравнений, существование решения необходимо проверять.

Выводы из данной статьи про решение систем линейных уравнений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое решение систем линейных уравнений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений