10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ ( Slant Transform ) кратко

Привет, Вы узнаете о том , что такое наклонное преобразование, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое наклонное преобразование, slant transform , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

В работах [24-26] предложено ортогональное преобразование, названное наклонным (slant transform). Это преобразование обладает следующими особенностями: 1) среди базисных векторов имеется вектор с одинаковыми компонентами (постоянный базисный вектор); 2) наклонный базисный вектор монотонно убывает от максимального до минимального значения скачками постоянной величины; 3) матрица преобразования обладает секвентным свойством; 4) существует быстрый алгоритм преобразования; 5) обеспечивается высокая степень концентрации энергии изображения. При длине вектора 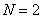наклонное преобразование совпадает с преобразованием Адамара второго порядка. Таким образом,

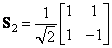. (10.7.1)

Матрица наклонного преобразования четвертого порядка формируется по следующему правилу:

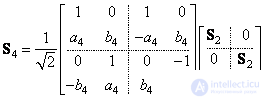, (10.7.2а)

или

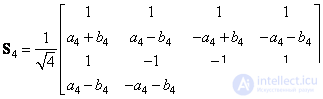, (10.7.2б)

где 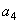и 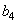- действительные коэффициенты, которые следует выбирать так, чтобы матрица 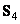была ортогональной, а величина скачков при изменении второго наклонного базисного вектора - постоянной. Из условия постоянства величины скачка можно найти, что 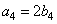. Из условия ортогональности 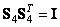следует, что 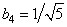. Об этом говорит сайт https://intellect.icu . Таким образом, матрица наклонного преобразования четвертого порядка имеет вид

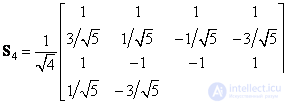. (10.7.3)

Нетрудно проверить, что матрица 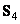является ортонормальной. Кроме того, она обладает секвентным свойством: число изменений знака возрастает с увеличением номера строки от 0 до 3.

Матрица наклонного преобразования при 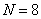имеет вид

. (10.7.4)

Как и при построении матрицы 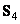, коэффициенты 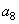и 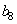подбираются так, чтобы наклонный базисный вектор убывал равномерными скачками, все строки матрицы являлись ортонормальными векторами, а сама матрица обладала секвентным свойством.

Обобщая соотношение (10.7.4), можно получить рекуррентную формулу, связывающую матрицы наклонного преобразования 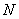-го и 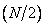-го порядка:

, (10.7.5)

где 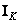- единичная матрица 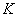-го порядка. Постоянные 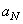и 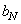можно найти из рекуррентных соотношений [26]

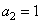, (10.7.6а)

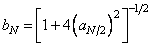, (10.7.6б)

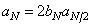(10.7.6в)

или по формулам

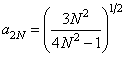, (10.7.7а)

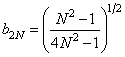. (10.7.7б)

На рис. 10.7.1 приведены графики базисных функций наклонного преобразования для 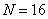. Пример спектра, получаемого при таком преобразовании, показан на рис. 10.7.2.

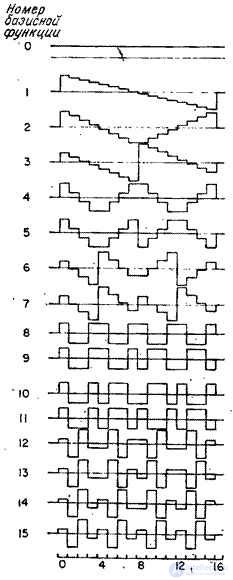
Рис. 10.7.1. Базисные функции наклонного преобразования при .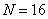

Рис. 10.7.2. Наклонное преобразование изображения «Портрет».

а - исходное изображение; б - результат преобразования в логарифмическом масштабе по оси амплитуд: в - результат преобразования с ограниченными наибольшими гармониками.

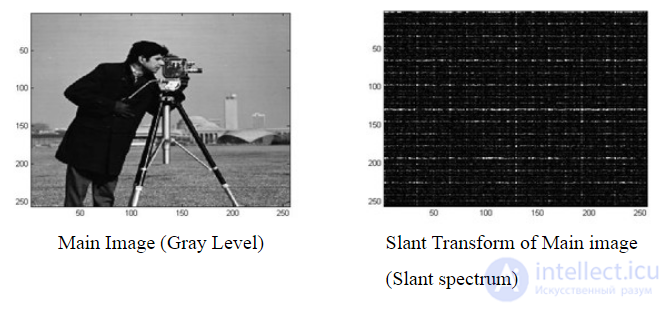
Пример наклонного преобразования Основное изображение (уровень серого) Наклонное преобразование основного изображения (наклонный спектр)

Вау!! 😲 Ты еще не читал? Это зря!

• Двумерные унитарные преобразования
• Операторы унитарных преобразований
• Синусное преобразование
• Косинусное преобразование
• Преобразование Хаара
• Преобразование Карунена-Лоэва

Выводы из данной статьи про наклонное преобразование указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое наклонное преобразование, slant transform и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений