11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ

Привет, Вы узнаете о том , что такое обработка с использованием преобразования, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обработка с использованием преобразования , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Двумерные линейные преобразования можно определить в виде ряда как

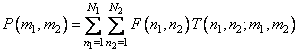.                  (11.1.1)

Это соотношение в векторной форме имеет вид

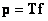.                      (11.1.2)

Ниже будет показано, что подобные линейные преобразования часто можно выполнить более эффективно, если вместо непосредственных вычислений по формулам (11.1.1) или (11.1.2) воспользоваться косвенными методами с применением двумерных унитарных преобразований.

На рис. 11.1.1 приведена структурная схема косвенного метода вычислений, называемого обобщенной линейной фильтрацией [1]. Массив 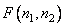, описывающий исходное изображение, подвергается здесь двумерному унитарному преобразованию, в результате которого получается массив коэффициентов преобразования 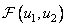. Затем составляется линейная комбинация этих коэффициентов, описываемая в общем случае формулой

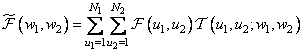,                 (11.1.3)

где 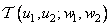 - ядро линейного фильтрующего преобразования. В заключение проводится обратное унитарное преобразование, чтобы получить обработанное изображение .

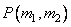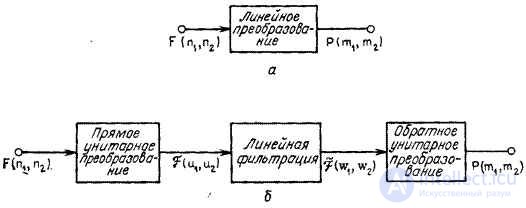
Рис. 11.1.1. Структура алгоритмов непосредственной обработки (а) и обобщенной линейной фильтрации (б).

Такой метод вычисления будет эффективнее, чем непосредственное вычисление по формуле (11.1.1), если существуют быстрые алгоритмы унитарного преобразования, а ядро 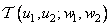 содержит большое количество нулевых элементов.

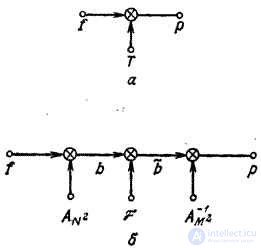
Рис. 11.1.2. Структура алгоритмов непосредственной обработки (а) и обобщенной линейной фильтрации (б) при векторном представлении изображений.

Процесс обобщенной линейной фильтрации можно также представить в векторной форме (рис. Об этом говорит сайт https://intellect.icu . 11.1.2). Для упрощения обозначений положим, что 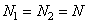, а 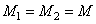. Тогда обобщенную линейную фильтрацию можно описать соотношениями

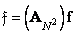,               (11.1.4а)

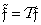,            (11.1.4б)

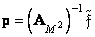,                      (11.1.4в)

где 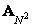 - матрица унитарного преобразования размера 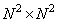,  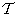- матрица оператора линейной фильтрации размер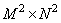а , а 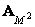 - матрица обратного унитарного преобразования размера 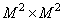. Как следует из соотношений (11.1.4), векторы исходного и обработанного изображений связаны между собой равенством

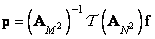.                   (11.1.5)

Приравнивая соотношения (11.1.2) и (11.1.5), найдем связь между матрицам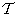и  и :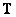

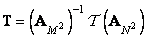,                     (11.1.6а)

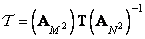.                      (11.1.6б)

При непосредственной обработке для выполнения вычислений по формуле (11.1.2) необходимо провести 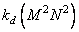 арифметических действий, где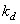 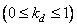  характеризует степень заполнения матрицы  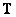ненулевыми элементами. При обобщенной линейной фильтрации общее число арифметических действий равно:

Прямое преобразование:

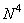  - при непосредственном вычислении;

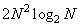  - при использовании быстрого преобразования.

Линейная фильтрация:

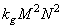  умножений.

Обратное преобразование:

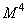  - при непосредственном вычислении;

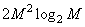  - при использовании быстрого преобразования.

Здесь 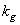 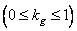 - коэффициент заполнения матрицы  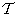ненулевыми элементами. Если  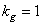и производится непосредственное вычисление унитарного преобразования, то очевидно, что обобщенная линейная фильтрация оказывается не столь эффективной, как непосредственная обработка. Однако, если применяются быстрые алгоритмы, подобные быстрому преобразованию Фурье (БПФ), обобщенная линейная фильтрация будет эффективнее, чем непосредственная обработка, если коэффициент заполнения матрицы  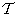удовлетворяет неравенству

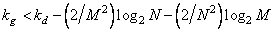.             (11.1.7)

Во многих случаях матрица 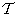 бывает разрежена и неравенство (11.1.7) выполняется. Вообще говоря, унитарные преобразования часто приводят к декорреляции элементов матрицы  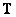и матрица  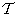оказывается разреженной. Кроме того, матрицу  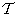часто удается разредить без внесения больших погрешностей, если заменить нулями ее малые по величине элементы [1].

В последующих разделах рассмотрена структура линейных операторов суперпозиции, свертки и псевдообращения, для того чтобы определить возможность применения метода обобщенной линейной фильтрации для осуществления этих операций.

Выводы из данной статьи про обработка с использованием преобразования указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое обработка с использованием преобразования и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений