10.5. Матрица Адамара, ПРЕОБРАЗОВАНИЕ АДАМАРА кратко

Привет, Вы узнаете о том , что такое преобразование адамара, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое преобразование адамара, матрица адамара, произведение кронекера , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

матрица адамара

Матрица Адамара — это квадратная матрица размера n×n, составленная из чисел 1 и −1, столбцы которой ортогональны, так что справедливо соотношение

где — это единичная матрица размера n. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.

Свойства матриц Адамара

На множестве матриц Адамара размера действует группа преобразований , порожденная инверсиями строк и столбцов (умножением на −1), а также перестановками строк и столбцов.

Две матрицы Адамара и называются эквивалентными, если существует элемент такой, что . Таким образом, все матрицы Адамара заданного размера разбиваются на классы эквивалентности.

Теорема 1. Существует алгоритм перечисления нормализованных матриц Адамара.

Теорема 2. Для порядков 1, 2, 4, 8, 12, 16, 20, 24 существует соответственно 1, 1, 1, 1, 2, 118, 6520, 43966313 (последовательность A147774 в OEIS) эквивалентных классов нормализованных матриц Адамара по отношению эквивалентности перестановок строк и столбцов.

Определение. Автотопией матрицы Адамара H называется элемент такой, что .

Теорема 3. Существует алгоритм вычисления группы автотопий матрицы Адамара.

Теорема 4. Существует алгоритм проверки эквивалентности двух матриц Адамара, находящий нужный элемент .

Теорема 5. Существуют полиномиально вычислимые функции на матрицах Адамара, инвариантные относительно действия группы , и позволяющие в определенных случаях различать неэквивалентные матрицы Адамара.

Теорема 6. Существует алгоритм, перечисляющий только по одной матрице из каждого эквивалентного класса, для всех матриц заданного размера (в стадии разработки).

Примеры

,

,

,

,

где , а означает произведение кронекера .

Использование матриц Адамара

• Иногда используются в рентгеновских телескопах с пространственным кодированием апертуры.
• Используются при кодировании информации (коды, исправляющие ошибки, ECC).

преобразование адамара

Преобразование Адамара [16, 17] основано на квадратной матрице Адамара [18], элементы которой равны плюс или минус единице, а строки и столбцы образуют ортогональные векторы. Об этом говорит сайт https://intellect.icu . Нормированная матрица Адамара -го порядка удовлетворяет соотношению

. (10.5.1)

Среди ортонормальных матриц Адамара наименьшей является матрица второго порядка

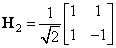. (10.5.2)

Недоказанная гипотеза Адамара утверждает, что матрица Адамара порядка 4k существует для каждого натурального k.

Известно, что если матрица Адамара порядка (где 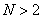) существует, то делится на 4 без остатка [19]. Пока не удалось определить, существуют ли матрицы Адамара для произвольных , удовлетворяющих этому условию, однако почти для всех допустимых , доходящих до 200, найдены правила построения соответствующих матриц. Наиболее просто удается построить такие матрицы при , где - целое. Если - матрица Адамара -го порядка, то матрица

(10.5.3)

также является матрицей Адамара, но порядка . На рис. 10.5.1 приведены матрицы Адамара четвертого и восьмого порядка, построенные с помощью соотношения (10.5.3).

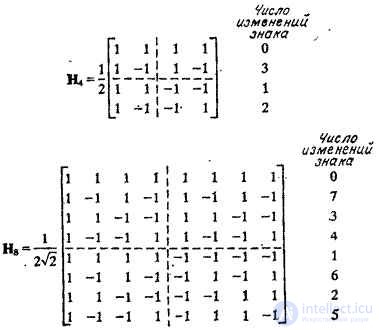
Рис. 10.5.1. Неупорядоченные матрицы Адамара четвертого и восьмого порядка.

Хармут [20] предложил частотную интерпретацию матриц Адамара, имеющих блочную структуру (10.5.3). Число изменений знака вдоль каждой строки матрицы Адамара, деленное на два, называется секвентой строки. Можно построить матрицу Адамара порядка , в которой число изменений знака в строках принимает значения от 0 до . Унитарные матрицы с такими характеристиками называются матрицами с секвентным свойством.

Строки матрицы Адамара, описываемой соотношением (10.5.3), можно рассматривать как последовательность отсчетов прямоугольных периодических колебаний (сигналов), период которых кратен 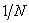. Подобные непрерывные функции, называемые функциями Уолша [21], связаны с импульсными функциями Радемахера [22]. Следовательно, матрица Адамара описывает преобразование, связанное с разложением функций по семейству прямоугольных базисных функций, а не по синусам и косинусам, характерным для преобразования Фурье.

Для симметричных матриц Адамара порядка двумерное преобразование Адамара можно представить в виде ряда

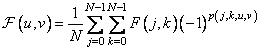, (10.5.4)

где

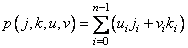. (10.5.5)

Переменные 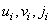и 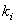равны цифрам в двоичном представлении чисел и соответственно. Так, например, если 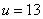, то и 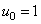. Если матрица Адамара упорядочена, т. е. строки ее переставлены в порядке возрастания секвенты, то существует другая форма записи преобразования Адамара. В этом случае

, (10.5.6)

где

, (10.5.7)

причем

(10.5.8)

Графики базисных функций преобразования Адамара с упорядоченной матрицей для 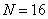представлены на рис. 10.5.2. Базисные изображения, образованные с помощью матричного произведения базисных векторов преобразования Адамара размера 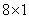, приведены на рис. 10.5.3. На рис. 10.5.4 дан пример преобразования Адамара (для упорядоченной матрицы Адамара).

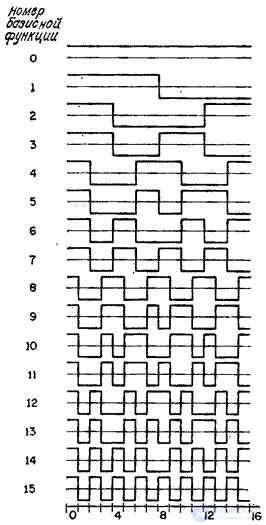
Рис. 10.5.2. Базисные функции преобразования Адамара при .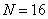

Рис. 10.5.3. Базисные изображения преобразования Адамара при .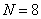

Черный цвет соответствует значению +1, белый - значению -1.

Рис. 10.5.4. Преобразование Адамара изображения «Портрет».

а - исходное изображение; б - спектр Адамара в логарифмическом масштабе по оси амплитуд; в - спектр с ограниченными наибольшими гармониками

Рис.10.5.4.2 Пример реставрации образа
Как видно из результатов, приведенных на рис.10.5.4.2, при одинаковых исходных условиях реставрация методом условной деконволюции в базисе преобразования Адамара дает лучшие результаты, чем деконволюции в базисе преобразования Фурье

Пример преобразования Адамара Основное изображение (уровень серого).
ГТ основного изображения (спектр Адамара).
Логарифмическая шкала спектра Адамара.

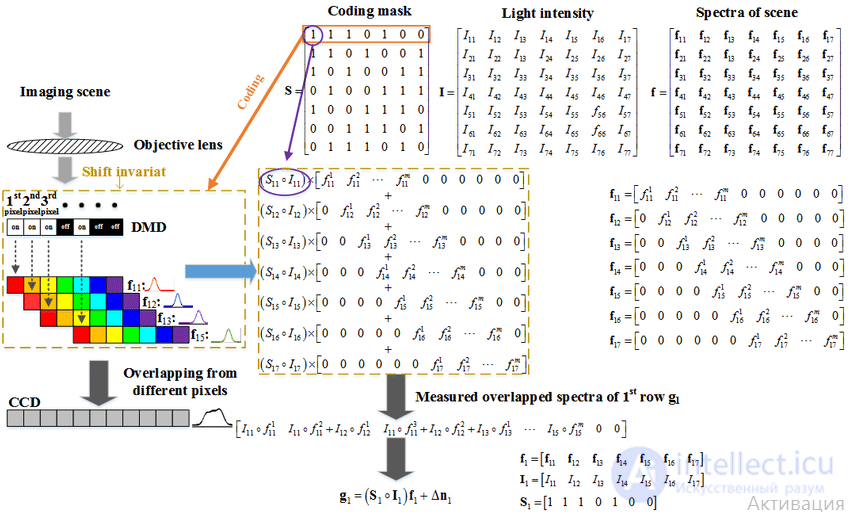
Рисунок 1. Принцип преобразования спектра с преобразованием Адамара.
На рисунке 1 S1 - это 1-я строка матрицы Адамара-S, I1 - интенсивность света 1-й строки. распределение сцены, f1 - спектр 1-й строки, f11 - спектр 1-го пикселя 1-й строки, m представляет его диапазон, а нули в спектре представляют собой инвариант сдвига, что делает обработка легко понять.

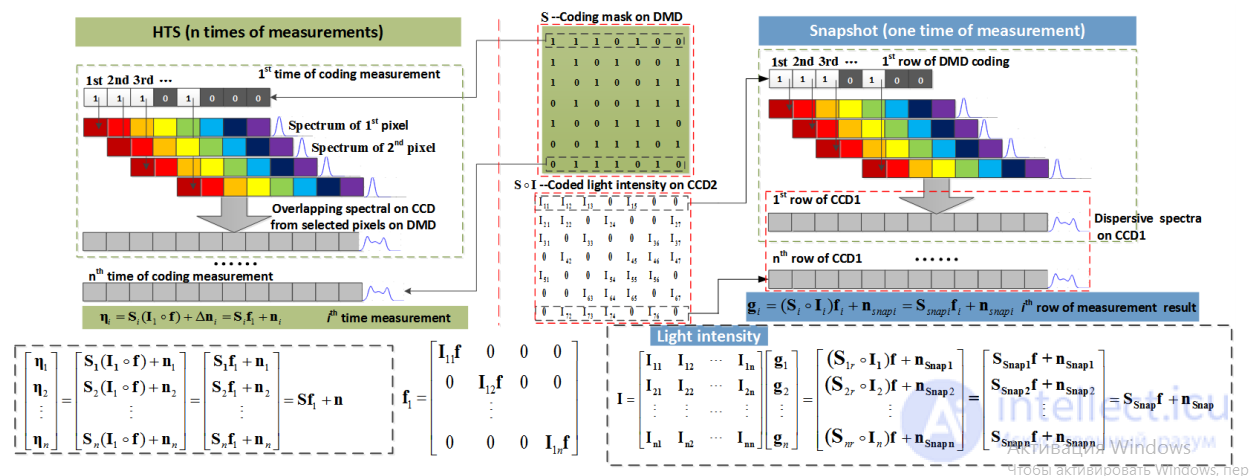
Рисунок 2. Принципиальное различие между традиционным ВТСП и спектрометром снимков суб-Адамара.

Основное различие между HTS моментальных снимков и традиционными HTS с множественным сканированием показано в рис 2

Вау!! 😲 Ты еще не читал? Это зря!

• Двумерные унитарные преобразования
• Операторы унитарных преобразований
• Косинусное и синусное преобразование
• Преобразование Хаара
• Преобразование Карунена-Лоэва
• Функция Уолша

Выводы из данной статьи про преобразование адамара указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое преобразование адамара, матрица адамара, произведение кронекера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений

Из статьи мы узнали кратко, но содержательно про преобразование адамара