1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ

Привет, сегодня поговорим про вероятностное описание непрерывных изображений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое вероятностное описание непрерывных изображений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Часто бывает удобно рассматривать изображение как реализацию случайного процесса. Введем порождающую изображения непрерывную случайную функцию 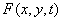 трех переменных — пространственных координат  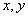и времени .

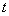Случайный процесс 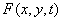 полностью описывается совместной плотностью вероятности

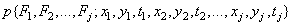
для 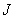 значений функции  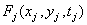в точках отсчета  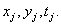Совместные плотности вероятности высокого порядка для изображений обычно не известны, и их в общем случае трудно моделировать. Для плотности вероятности первого порядка  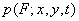иногда удается подобрать удачную модель из физических соображений или на основе измеренных гистограмм. Например, плотность вероятности первого порядка случайного шума в электронных преобразователях изображений хорошо моделируется гауссовой плотностью:

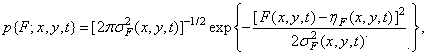     (1.9.1)

где параметры 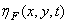 и 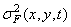 есть среднее и дисперсия шума. Гауссова плотность может также с приемлемой точностью служить моделью плотности вероятности коэффициентов унитарных преобразованийизображений. Плотность вероятности яркости должна быть односторонней, так как яркость принимает только положительные значения. В качестве моделей плотности вероятности яркости применяются плотностьраспределения вероятностей Рэлея

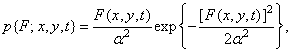                            (1.9.2а)

плотность логарифмически нормального распределения

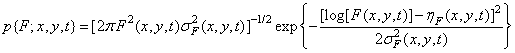     (1.9.2б)

и плотность экспоненциального распределения

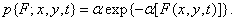                               (1.9.2в)

Эти плотности определены при 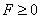, причем  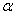- постоянная. Двусторонняя экспоненциальная, или лапласова, плотность

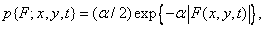     (1.9.3)

где 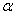 - постоянная, часто используется как модель плотности вероятности разностей отсчетов функции, описывающей изображение. Об этом говорит сайт https://intellect.icu . Наконец, плотность равномерного распределения

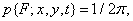
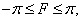                                      (1.9.4)

Есть обычная модель для флуктуаций фазы случайного процесса. Для описания случайного процесса можно использовать так же условные плотности вероятности. Условная плотность вероятности значения функции 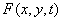 в точке  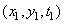при заданном значении этой функции в точке  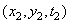определяется как

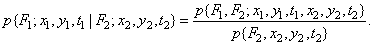     (1.9.5)

Аналогично определяются условные плотности более высокого порядка.

Другой способ описания случайного процесса состоит в вычислении средних по ансамблю. Первый момент, или среднее значение функции 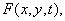 равен

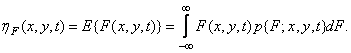                        (1.9.6)

Второй момент, или автокорреляционная функция, определяется как

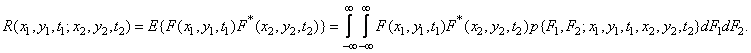   (1.9.7)

Автоковариационная функция изображения определяется как 

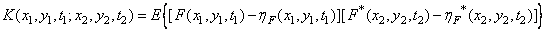    (1.9.8а)

Автоковариационная и автокорреляционная функции связаны соотношением

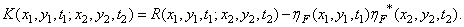   (1.9.8б)

наконец, дисперсия процесса 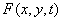 есть

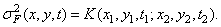                                    (1.9.9)

Случайный процесс, порождающий изображения, называется стационарным в строгом смысле, если его моменты не зависят от переноса начала координат в пространстве или времени. Процесс называется стационарным в широком смысле, если он имеет постоянную среднюю яркость, а его автокорреляционная функция зависит от разностей координат 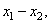 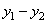, , 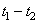но не от самих координат. Для стационарного  процесса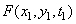 

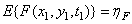                                                                  (1.9.10а)

и

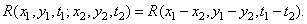     (1.9.10б)

Выражение для автокорреляционной функции можно записать в виде

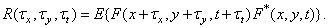     (1.9.11)

Так как

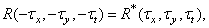                                        (1.9.12)

для действительной функции 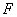 автокорреляционная функция является действительной и четной.Энергетический спектр стационарного изображения по определению есть результат трехмерногопреобразования Фурье его автокорреляционной функции:

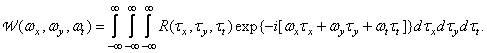     (1.9.13)

Во многих изображающих системах пространственные и временные процессы формирования изображений разделяются. В этом случае стационарную автокорреляционную функцию можно записать как

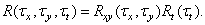                          (1.9.14)

Часто для упрощения вычислений пространственную автокорреляционную функцию представляют в виде произведения автокорреляционных функций для каждой пространственной переменной:

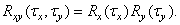                                                  (1.9.15)

В изображениях объектов, созданных человеком, часто встречаются горизонтальные и вертикальные структуры, поэтому аппроксимация автокорреляционной функции произведением (1.9.15) оказывается вполне приемлемой. В изображениях естественных сцен обычно нет преобладающих направлений корреляции. Пространственная автокорреляционная функция таких изображений близка к функции с вращательной симметрией и не является поэтому разделимой.

Часто моделью изображения служат реализации двумерного марковского процесса первого порядка. Автоковариационная функция такого процесса имеет вид

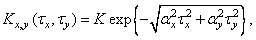                        (1.9.16)

где 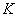,  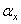и 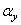 — масштабные множители. Соответствующий энергетический спектр равен

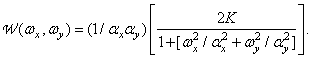     (1.9.17)

Часто делается упрощающее предположение, что автоковариационная функция марковского процесса может быть представлена в виде

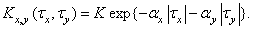                         (1.9.18)

Энергетический спектр этого процесса есть

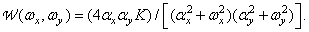       (1.9.19)

При детерминированном описании изображений были определены средние по пространству и времени. При статистическом описании также определяется среднее по ансамблю. Возникает вопрос: как связаны друг с другом пространственно-временные средние и средние по ансамблю? Ответ состоит в том, что для некоторых случайных процессов, называемых эргодическими, пространственно-временные средние и средние по ансамблю равны. Очень трудно доказать эргодичность случайного процесса в общем случае. Обычно достаточно определить эргодичность второго порядка, при которой моменты первого и второго порядка, полученные пространственно-временным усреднением, равны соответствующим моментам при усреднении по ансамблю.

Надеюсь, эта статья про вероятностное описание непрерывных изображений, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое вероятностное описание непрерывных изображений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений