8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Привет, Вы узнаете о том , что такое приближенные решения несовместных систем линейных уравнений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое приближенные решения несовместных систем линейных уравнений , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.

Несовместность системы уравнений 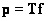 означает, что ни для одной из возможных оценок  система не будет переходить в тождество при подстановке  вместо 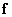. В таких случаях систему уравнений можно преобразовать к виду

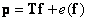                                                 (8.6.1)

где 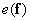 - вектор ошибки, зависящий от 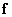. Найдем теперь такое значение оценки , при котором оказывается минимальной величина ошибки, выражаемая двумя эквивалентными соотношениями:

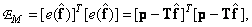                          (8.6.2а)

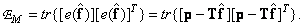        (8.6.2б)

Пусть символ 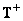 обозначает псевдообратную матрицу, с помощью которой получается оценка

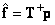                                                            (8.6.3)

Прибавив и отняв произведение 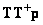 внутри обеих скобок соотношения (8.6.2а), получим

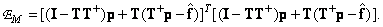     (8.6.4)

После перемножения имеем

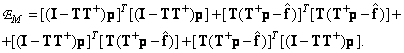      (8.6.5)

Два перекрестных члена будут равны нулю, есл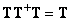и  и 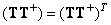. Об этом говорит сайт https://intellect.icu . Однако при выполнении этих условий матрица  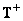является матрицей обращения методом наименьших квадратов, т. е. 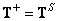. Тогда ошибка будет равна сумме двух положительных слагаемых:

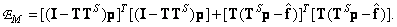     (8.6.6)

Второй член равенства (8.6.6) превращается в нуль, так как 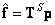. Следовательно, ошибка уменьшается до величины

                  (8.6.7а)

или, что то же самое,

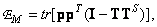          (8.6.7б)

Как и ожидалось, ошибка равна нулю, если .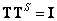

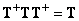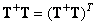Решение, полученное псевдообращением по методу наименьших квадратов, может быть не единственным. Если при псевдообращении ввести дополнительные условия  и , при которых матрица  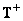является обобщенной обратной (т. е. 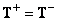), то можно показать, что оценка, полученная с помощью этой матрицы (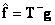), является  решением с минимальной нормой в том смысле, что

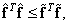                        (8.6.8)

где 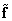 - произвольная оценка, найденная методом наименьших квадратов. Если обобщенная обратная матрица  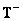имеет ранг  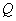и удовлетворяет определению (8.3.5), то произведение  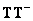не обязательно равно единичной матрице, а ошибку можно найти из соотношений (8.6.7). Если же матрица  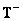имеет ранг 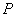, т. е. соответствует определению (8.3.6), то и  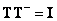ошибка равна нулю.

В последующих главах будет показано, как данные теоретические положения применяются для исправления, анализа и кодирования изображений.

Выводы из данной статьи про приближенные решения несовместных систем линейных уравнений указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое приближенные решения несовместных систем линейных уравнений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений