Лекция
Game: Perform tasks and rest cool.6 people play!
Play gameПривет, сегодня поговорим про двумерное преобразование фурье, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое двумерное преобразование фурье , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
Методом двумерного преобразования Фурье (two-dimensional Fourier transform - 2-DFT) является преобразование Фурье, произведенное над двумерным массивом данных. Рассмотрим двумерный массив данных, показанный на рисунке.
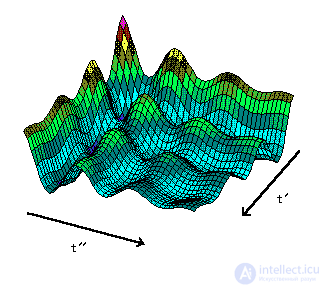
Эти данные имеют два измерения: t' и t". Преобразование Фурье над данными производится сначала в одном, а затем в другом направлениях. Первая часть преобразований Фурье проводится в t' измерении для получения f' на t" множества данных.
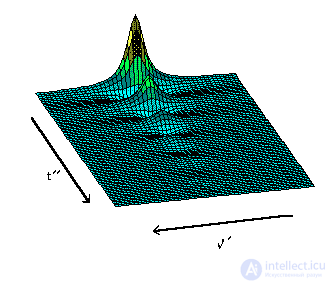
Вторая часть преобразований Фурье производится в t" измерении для получения f' на f" множества данных. 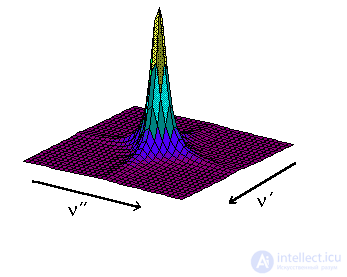
двумерное преобразование фурье необходимо для проведения МРТ на современном уровне. В МРТ, данные собираются в эквиваленте t' и t" измерениям, называемом К-пространстве. Эти исходные данные преобразуются для получения изображения, которое эквивалентно описанным ранее f' на f" данным.
В результате двумерного преобразования Фурье функции 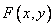 , описывающей изображение, получается спектр этого изображения, который определяется как
, описывающей изображение, получается спектр этого изображения, который определяется как
 , (1.6.1)
, (1.6.1)
где 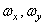 - пространственные частоты, а
- пространственные частоты, а 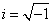 . Если обозначить оператор преобразования Фурье через
. Если обозначить оператор преобразования Фурье через 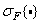 , то можно записать
, то можно записать
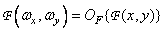 . (1.6.2)
. (1.6.2)
В общем случае спектр 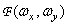 есть комплексная величина. Его можно разложить на действительную и мнимую части:
есть комплексная величина. Его можно разложить на действительную и мнимую части:
 (1.6.3а)
(1.6.3а)
или представить с помощью амплитуды и фазы:
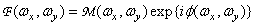 , (1.6.3б)
, (1.6.3б)
где
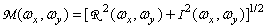 , (1.6.4а)
, (1.6.4а)
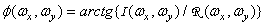 . (1.6.4б)
. (1.6.4б)
Game: Perform tasks and rest cool.6 people play!
Play game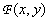 является абсолютная интегрируемость этой функции, т.е. Об этом говорит сайт https://intellect.icu . условие
является абсолютная интегрируемость этой функции, т.е. Об этом говорит сайт https://intellect.icu . условие
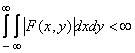 . (1.6.5)
. (1.6.5)
Исходная функция 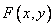 может быть восстановлена обратным преобразованием Фурье:
может быть восстановлена обратным преобразованием Фурье:
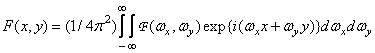 . (1.6.6a)
. (1.6.6a)
Это соотношение в операторной форме можно записать как
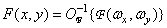 . (1.6.6б)
. (1.6.6б)
Поскольку ядро двумерного преобразования Фурье разделимо, это преобразование может быть выполнено в два этапа. Сначала находится
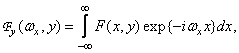 (1.6.7)
(1.6.7)
а затем
Game: Perform tasks and rest cool.6 people play!
Play game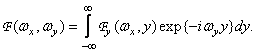 (1.6.8)
(1.6.8)
Ниже приводятся несколько полезных свойств двумерного преобразования Фурье. Их доказательства можно найти в книгах [1, 2].
Функциональные свойства
Если функция 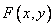 разделима по пространственным переменным, так что
разделима по пространственным переменным, так что
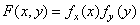 , (1.6.9)
, (1.6.9)
то
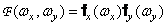 , (1.6.10)
, (1.6.10)
где 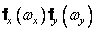 - одномерные фурье-спектры функций
- одномерные фурье-спектры функций 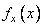 ,
, 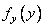 . Если
. Если 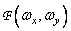 есть фурье-спектр функции
есть фурье-спектр функции 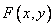 , то
, то 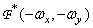 является фурье-спектром функции
является фурье-спектром функции  . (Звездочка обозначает комплексную сопряженность.) Если функция
. (Звездочка обозначает комплексную сопряженность.) Если функция 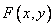 симметрична, т.е.
симметрична, т.е. 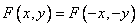 , то
, то 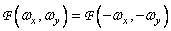 .
.
Линейность
Оператор преобразования Фурье линеен:
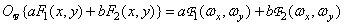 , (1.6.11)
, (1.6.11)
где  – постоянные.
– постоянные.
Изменение масштаба
Изменение масштаба пространственных приводит к обратному изменению масштаба пространственных частот и пропорциональному изменению значений спектра:
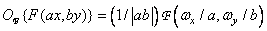 . (1.6.12)
. (1.6.12)
Следовательно, сжатие вдоль одной из осей плоскости  приводит к растяжению вдоль соответствующей оси частотной плоскости и наоборот. Происходит также пропорциональное изменение значений спектра.
приводит к растяжению вдоль соответствующей оси частотной плоскости и наоборот. Происходит также пропорциональное изменение значений спектра.
Сдвиг
Сдвиг (изменение координат) на исходной плоскости приводит к фазовым изменения на частотной плоскости:
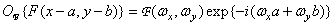 (1.6.13а)
(1.6.13а)
Наоборот, сдвиг на частотной плоскости вызывает фазовые изменения исходной функции:
Game: Perform tasks and rest cool.6 people play!
Play game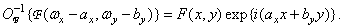 (1.6.13б)
(1.6.13б)
Свертка
Фурье-спектр функции, полученный в результате свертки двух функций, равен произведению спектров исходных функций:
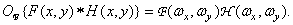 (1.6.14)
(1.6.14)
Обратная теорема утверждает, что
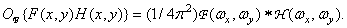 (1.6.15)
(1.6.15)
Теорема Парсеваля
Два представления энергии изображения – через функцию 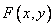 и фурье-спектр
и фурье-спектр 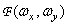 - связаны следующим образом:
- связаны следующим образом:
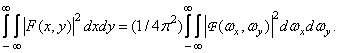 (1.6.16)
(1.6.16)
Game: Perform tasks and rest cool.6 people play!
Play gameТеорема о спектре автокорреляционной функции
Фурье-спектр двумерной автокорреляционной функции изображения равен квадрату модуля фурье-спектра этого изображения:
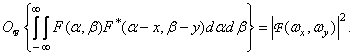 (1.6.17)
(1.6.17)
Спектры пространственных производных
Фурье-спектры первых пространственных производных функции 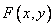 связаны с ее фурье-спектром следующими соотношениями:
связаны с ее фурье-спектром следующими соотношениями:
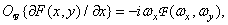 (1.6.18a)
(1.6.18a)
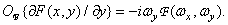 (1.6.18б)
(1.6.18б)
Следовательно, спектр лапласиана равен
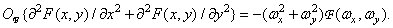 (1.6.19)
(1.6.19)
Надеюсь, эта статья про двумерное преобразование фурье, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое двумерное преобразование фурье и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка изображений
Из статьи мы узнали кратко, но содержательно про двумерное преобразование фурье
Комментарии
Оставить комментарий
Цифровая обработка изображений
Термины: Цифровая обработка изображений