Функция полезности - ее определение, исследование и характеристики. оптимизация кратко

Привет, Вы узнаете о том , что такое функция полезности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое функция полезности, кардинализм, ординализм, кривая безразличия, второй закон госсена, задача потребительского выбора, задача рационального поведения потребителя на рынке , настоятельно рекомендую прочитать все из категории Теория принятия решений.

функция полезности — функция, с помощью которой можно представить предпочтения потребителя на множестве допустимых альтернатив. Числовые значения функции помогают упорядочить альтернативы по степени предпочтительности для потребителя. Большее значение соответствует большей предпочтительности. В современной ординалисткой теории полезности сами числа значения не имеют — важны только отношения «больше», «меньше» и «равно».

Не каждое отношение предпочтения можно представить с помощью функции полезности. Однако для используемых в экономических моделях предпочтений такая функция существует. Существование функции позволяет использовать математический анализ при решении оптимизационных задач в экономике. Например, при решении задачи потребителя . Без использования функции полезности решение такой задачи становится затруднительным.

Множество задания бинарного отношения предпочтения X может иметь довольно сложную структуру, и поэтому сравнение между собой его элементов тоже может оказаться сложной задачей. Однако во многих случаях можно каждому элементу х е X сопоставить некоторую числовую характеристику, обозначающую его «полезность».

Функция полезности является мерой соотношения между объемами потребляемых благ и уровнем полезности:

U = U (y1, y2,…, y n);
где U – полезность набора благ,
а y1, y2,…, y n- объемы потребления благ.

Функция полезности является очень удобным вспомогательным средством, которое открывает возможность использования теории оптимизации при решении задачи потребителя. Без использования функции полезности решение такой задачи с математической точки зрения может быть затруднительным. Несмотря на некоторую ограниченность подхода, функция полезности является неотъемлемой частью большинства современных экономических моделей

Формальное определение

Пусть дано множество допустимых альтернатив , на котором определено отношение предпочтения . Тогда вещественнозначная функция называется функцией полезности, если выполнено условие :

Большее значение функции полезности означает большую предпочтительность альтернативы в смысле предпочтения, которое эта функция представляет. С математической точки зрения функция полезности является способом скалярного ранжирования.

Определение

Пусть на множестве Xзадано отношение предпочтения (>). Функцией полезности называется функция и . X -* 9?, заданная на X таким образом, что для произвольных элементов х, у е X верны следующие соотношения: х предпочтительнее у (х> у) тогда и только тогда, когда и(х) > и(у).

При этом говорят, что функция полезности и порождает отношение предпочтения на X и часто пишут .г у.

Поскольку множество вещественных чисел 9? упорядочено, то сравнение числовых характеристик объектов позволит сравнивать и сами эти объекты. Так, например, в соревнованиях по прыжкам в длину полезность прыжка определяется его дальностью.

Пример определения значения функции полезности. Предположим, что необходимо принять решение о том, кто из студентов учебной группы, описанной в примере (*), примет участие в олимпиаде по математике. Введем функцию полезности гг, ставящую каждому студенту в соответствие его средний балл, полученный по математическим предметам за все годы обучения. Такая функция порождает отношение предпочтения на множестве студентов С следующим образом: студент ?, предпочтительнее студента ?2, если балл студента gl выше балла студента Предположим, что средний балл Иванова 3,8, Петрова — 5, Семенова — 5. Тогда Петров будет более предпочтителен для участия в олимпиаде, чем Иванов. При этом по данному критерию безразлично кого выбирать — Петрова или Семенова. Для выбора среди этих студентов нужен другой критерий.

Если существует хотя бы одна функция полезности, то таких функций существует бесконечное множество, поскольку композиция и с любой возрастающей функцией g, определенной на множестве значений функции и, т.е^(и(х)), также будет функцией полезности, порождающей то же самое отношение предпочтения на X. При этом некоторые функции могут быть более удобны с точки зрения своих свойств, например, могут быть линейными, дифференцируемыми или обладать другими подходящими свойствами.

Следует заметить, что понятие полезности применимо не к любым бинарным отношениям. Такую функцию нельзя построить для бинарных отношений, не являющихся ацикличными, таких как отношение = «родственники», описанное в примере (*). Кроме того, если понятие безразличия для ЛПР, как упоминалось в предыдущем параграфе, не обладает свойством транзитивности, то в таких случаях тоже нельзя построить функцию полезности.

кардинализм и ординализм

Современная микроэкономика опирается на ординалистский подход к моделированию потребительского поведения и выбора. В соответствии с ним, числовые значения функции полезности не играют роли, важны лишь порядок «больше-меньше». Если значение функции полезности для одной из альтернатив выше, то эта альтернатива является более предпочтительной для потребителя. При этом разность значений или частное от их деления не несет никакой информации . Противоположным является кардиналистский подход, при использовании которого числовые значения, наоборот, несут информацию о полезности. Кардиналистcкий подход неявно предполагает существование эталона полезности, то есть универсальной единицы, с которой можно производить сравнения. Об этом говорит сайт https://intellect.icu . Именно такое понимание полезности использовал создатель философии утилитаризма Иеремия Бентам .

Современные экономисты исходят из того, что представления о полезности субъективны, поэтому непосредственное их сравнение невозможно. Поэтому для оценки совместного благосостояния потребителей используется концепция эффективности по Парето. Исключением являются квазилинейные предпочтения. Они предполагают существование счетного товара (англ. numeraire), который является аналогом денег. Тогда суммирование и другие операции над полезностью становятся возможными.

Условия существования функции полезности

Для того чтобы предпочтения можно было представить в виде функции полезности, необходимо, чтобы само предпочтение было рациональным, то есть отвечало аксиомам полноты и транзитивности.

Достаточные условия зависят от самого множества допустимых альтернатив и от свойств предпочтений. Если множество {\displaystyle X} конечно или счетно, а отношение предпочтения рационально, то существует функция полезности, которая представляет эти предпочтения.

Если множество несчетно, то приходится дополнительно требовать непрерывности предпочтений. В этом случае теорема Дебре гарантирует существование функции полезности. При этом функция полезности является непрерывной. Непрерывность является необходимым условием существования функции полезности, представляющей рациональное предпочтение, но оно не является достаточным. Так, например, функция полезности (целая часть числа) представляет предпочтения, которые не являются непрерывными. Сама функция при этом также разрывна.

Часто на предпочтения накладываются дополнительные условия, чтобы получить функции с теми или иными свойствами. Так, можно требовать монотонности, локальной ненасыщаемости и выпуклости. Эти свойства предпочтений отражаются в свойствах функции полезности. Например, монотонность предпочтений ведет в монотонности функции, а выпуклость предпочтений делает функцию квазивогнутной.

Теорема Дебре

Для любых рациональных и непрерывных предпочтений на существует представляющая их непрерывная функция полезности .

Свойства функции полезности

Пусть задана строго возрастающая функция и пусть } — функция полезности. Тогда композиция функций также является функцией полезности, представляющей то же самое отношение предпочтения . Отметим, что не обязана быть непрерывной .

Если множество является выпуклым, то функция полезности будет квазивогнутой.

Если предпочтения отвечают свойству монотонности (строгой монотонности), то функция будет монотонной (строго монотонной).

Свойство убывающей предельной полезности является следствием вогнутости функции полезности. Если функция дважды дифференцируема, то свойство означает, что вторая частная производная такой функции отрицательна.

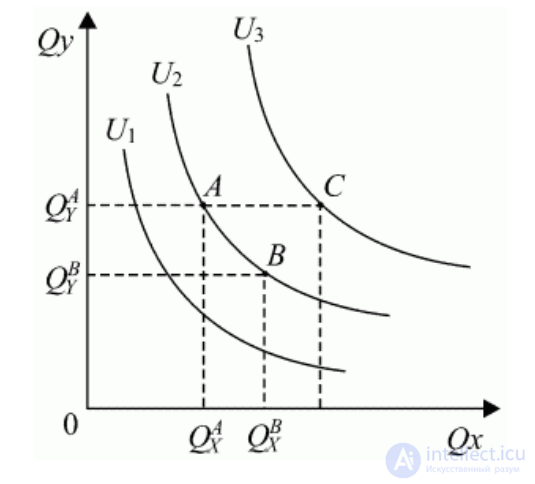
кривая безразличия — это линия (поверхность, гиперповерхность) уровня функции полезности.

Важнейшие примеры функций полезности

Постоянная эластичность замещения

Одной из важнейших функций полезности является CES-функция. Аббревиатура CES (англ. constant elasticity of substitution) означает постоянную эластичность замещения альтернатив. Функция имеет следующий вид для двумерного случая.

При разных значениях параметра {\displaystyle \rho } можно получить частные случаи CES-функции.

Если , то функция является линейной и описывает совершенные заменители. В этом случае предельная норма замещения равна отношению параметров .

Если , то получается функция Леонтьева, которая описывает совершенные дополнители. Предельная норма замещения в этом случае бесконечна.

При получается функция Кобба-Дугласа, если наложить дополнительное условие .

Отношение к риску

Важными примерами функций полезности являются функции с постоянным абсолютным и относительным показателем отношения к риску. Функция с постоянным абсолютным показателем отношения к риску (англ. CARA — constant absolute risk aversion):

Абсолютная мера Эрроу-Пратта для такой функции равна: .

Функция с постоянным относительным показателем отношения к риску (англ. CRRA — constant relative risk aversion):

Относительная мера Эрроу-Пратта для такой функции равна: .

Функция полезности Стоуна-Гири

Функция полезности Стоуна-Гири определяется следующим образом.

Для , функция полезности Стоуна-Гири превращается в функцию Кобба-Дугласа общего вида. Функция полезности Стоуна-Гири лежит в основе линейной системы расходов.

Основные характеристики функции полезности

Средняя полезность - это отношение общей полезности к количеству потребленных единиц блага

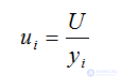
Предельная полезность (MU) — это увеличение общей полезности при потреблении одной дополнительной единицы блага.

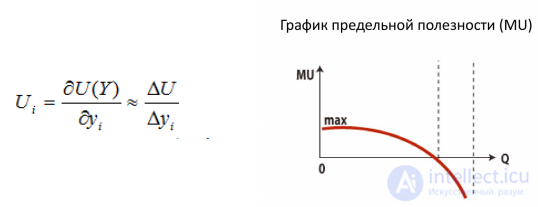
Коэффициент эластичности - величина, равная отношению предельной полезности к средней.

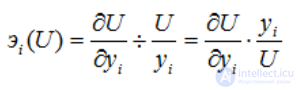
Если эластичность > 1, то функция полезности называется эластичной (по yi);
если < 1, то функция полезности называется неэластичной (по yi); если = 1, то говорят, что функция имеет единичную эластичность (по yi).
Коэффициент полной эластичности функции U:

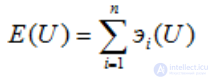
Предельная норма замены благ i и j:

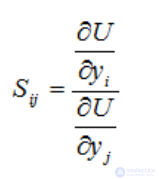
Пример:

Предположим, что имеется 5 наборов товаров: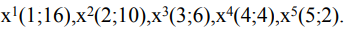
с одинаковой полезностью, т.е. .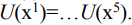

Пусть первый вид товара - одежда, второй - продукт питания.

Эти точки лежат на одной кривой безразличия.

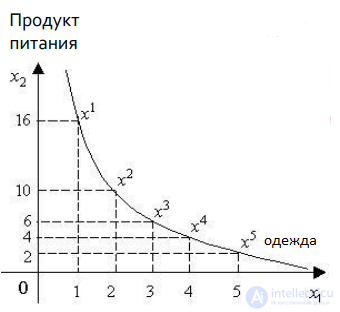
Как следует из графика, замена набора х1 набором х2 требует отказа от 6 единиц продуктов питания взамен на одну единицу одежды; замена х2 на х3
- отказа от 4 единиц продуктов питания ради одной единицы одежды и т.д.

Кривая безразличия

Кривая безразличия – это линия, каждая точка которой представляет комбинацию двух товаров, которые имеют для потребления одинаковую общую полезность.

Подходы к исследованию функции полезности

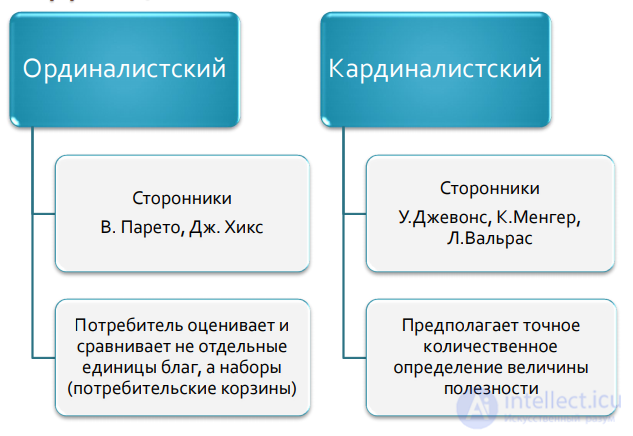
Ординалистский и Кардиналистский

Кардиналистский - Предполагает точное количественное определение величины полезности

Ординалистский - Потребитель оценивает и сравнивает не отдельные единицы благ, а наборы (потребительские корзины)

Оптимизация полезности с точки зрения экономической теории

второй закон госсена : чтобы получить максимум полезности доход потребителя должен быть распределен таким образом, чтобы каждая последняя денежная единица, затраченная на приобретение каждого вида продуктов, приносила бы одинаковую добавочную (предельную) полезность

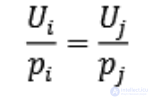
задача потребительского выбора

Задача потребительского выбора ( задача рационального поведения потребителя на рынке ) заключается в выборе такого потребительского набора, который максимизирует его функцию полезности при заданном бюджетном ограничении. Модель поведения потребителей:

Пример задачи нелинейного программирования:

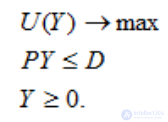
Найти оптимальный набор потребителя 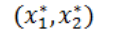с бюджетом М = 12 и функцией полезности U = x₁+x₂ при ценах p₁ = 2 и p₂ = 3

Составим ЭММ задачи:

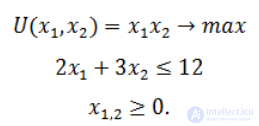
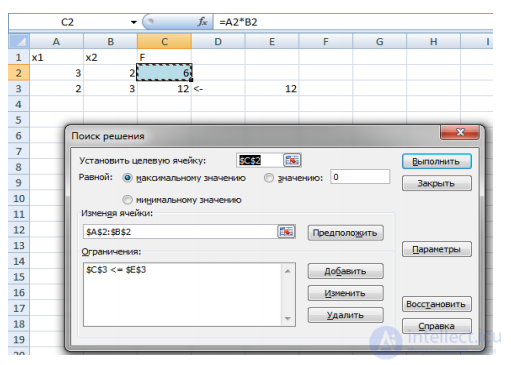
Для решения задачи подключаем инструмент Поиск решения в Excel:

Вау!! 😲 Ты еще не читал? Это зря!

• Полезность
• Предельная полезность
• Отношение предпочтения
• Множество допустимых альтернатив
• Предельная норма замещения
• Эластичность замещения
• Моральное ожидание
• Линейная система расходов

Исследование, описанное в статье про функция полезности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое функция полезности, кардинализм, ординализм, кривая безразличия, второй закон госсена, задача потребительского выбора, задача рационального поведения потребителя на рынке и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений