Лекция
Привет, Вы узнаете о том , что такое Условия Парето-оптимальности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Условия Парето-оптимальности , настоятельно рекомендую прочитать все из категории Теория принятия решений.
При т > 3 геометрические способы проверки условий Парето-оптимальности утрачивают наглядность, а потому и эффективность. Аналогом угла предпочтения становится область трехмерного пространства (г/,, у2, у3), определяемая неравенствами г/, > у*, у2 > у2, у3 > у3, за исключением самой точки (у*, у*2, у3). Геометрически эту область можно трактовать как первый октант трехмерного пространства (т.е. одну из восьми частей, на которые пространство делят три координатные плоскости), сдвинутый путем параллельного переноса от начала координат к точке (у*, у, у3). Область называют конусом предпочтения имея в виду не конус в обычном понимании (как тело вращения, образуемое вращением прямого луча вокруг оси), а конус в действительном векторном пространстве Е, определяемый как множество КаЕ такое, что ХК с К для любого X > О . Сложность пространственных представлений лишает процедуру геометрического построения множества Парето — Эджворта той наглядности, которая присуща углу предпочтения. Поэтому для т = 3 и для большего числа критериев геометрическая интерпретация обычно теряет преимущества. Образ множества 11арето — Эджворта становится участком поверхности (или гиперповерхности для т > 3), форма которого может оказаться сложной и недоступной для наглядного представления.
Таким образом, геометрическая проверка условий Парето-оптимальности отступает на второй план, а первоочередными становятся аналитические и численные методы.
Приведем относительно несложный и довольно общий пример, связанный с реальной финансово-экономической деятельностью и иллюстрирующий характерные для таких ситуаций проблемы.
Пример: рассматривается многокритериальная задача, которая возникает при хеджировании (передаче ценового риска) — использовании опционов будущих доходов в операциях продажи актива.
Опционы — это контракты, которые гарантируют своему покупателю право (но не обязательство) продать (или купить) какие-либо активы но оговоренной цене, тем самым обеспечивая способ защиты от неблагоприятных изменений цен. Об этом говорит сайт https://intellect.icu . В то же время они оставляют возможность получить прибыль при благоприятных изменениях цен. Доход заранее не известен — он представляет собой случайную величину, зависящую от неопределенности рыночных условий. Задан лишь прогноз, согласно которому минимальный уровень дохода V обеспечивается с вероятностью 1 - а. Задача состоит в оптимизации но трем критериям : получить максимальный уровень величины V при минимальной вероятности ошибки и минимальных затратах (2 на покупку. Затруднения при анализе связаны с тем, что графики выплат, соответствующие опционам, сложнее но форме, чем аналогичные графики для фьючерсных и форвардных контрактов.
Множество Парето — Эджворта, отвечающее данной многокритериальной задаче, построено с помощью аналитических оценок в работе И. И. Гасанова и Ф. И. Ерешко для некоторого класса встречающихся на практике ограничений и приведено на рис. 9.5. Поскольку для трех критериев V, а и (2 множество Парето — Эджворта О трехмерно, рис. 9.5 демонстрирует проекцию 19 на плоскость двух критериев: уровня дохода V и а-квантиля 5а функции распределения Е, значение которой в заданной точке равно а. Ось третьего критерия (2 направлена перпендикулярно приведенной на рис. 9.5 плоскости, и ее изображение лишь затруднило бы восприятие иллюстрации.
Отметим, что критерий 5а, требующий минимизации, в отличие от всех предыдущих примеров, не преобразован согласно замечанию вначале главы, т.е. направление оптимизации здесь не вправо и вверх (как в прежних случаях), а влево и вверх. Множество Парето — Эджворта О оказывается объединением трех подмножеств ?),, В2 и Г)3, два из которых (Г)2 и Г)3) проектируются в прямые: 1)9 — в ось ординат, а 03 — в прямую, проходящую че-
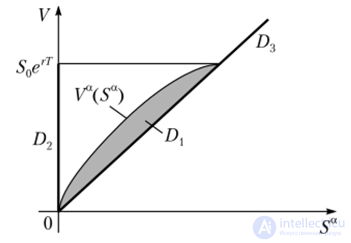
Рис 95. Проекция множества Парето-оптимальных оценок в задаче о хеджировании опционов рсз начало координат. Однако в трехмерном пространстве О., и Ол представляют собой области в плоскостях, проведенных через эти прямые и ось (). Множество 1)[ ограничено в плоскости рис. 9.5 кривой Е“(5“), где Е“(5°) определяется как корень уравнения Х(Х0(У)) = 5“ относительно переменной V, где через '?(X) обозначено выражение
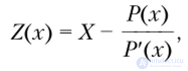
в котором Р(х) — заданная цена актива.
Итак, пример рассмотрения многокритериальной задачи подтверждает, что даже при наличии аналитического решения геометрическая интерпретация уже в трехмерном критериальном пространстве не обладает наглядностью и не способна в должной мере дать визуальное представление при проектировании на плоскость.
Обратите внимание!
Условия Парето-оптималыюсти проверяются проще всего геометрически с помощью угла предпочтения в задачах с двумя критериями. Но в многокритериальных задачах геометрические способы проверки условий Парето-оптималыюсти малопригодны и не обеспечивают простого и наглядного представления проблемы для принятия решений. Более того, проектирование многомерной картины на плоскость двух критериев может приводить к ошибкам1.
Таким образом, условия Парето-оптимальности при т > 3 требуют иных методов анализа.
Исследование, описанное в статье про Условия Парето-оптимальности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Условия Парето-оптимальности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений