Бинарные отношения.

Привет, Вы узнаете о том , что такое Бинарные отношения., Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Бинарные отношения. , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Определение

Говорят, что на произвольном множестве X задано бинарное отношение <р (или >Ху или V), если определено некоторое подмножество ф декартова произведения множества X на себя, т.е. ф с X X X. При этом говорят, что элементы х'у х" е X находятся в бинарном отношении ф, если (х х") ? ф, что записывается в следующем виде: дг'фл:", или х' >хх", или х' Vх".

Обратите внимание!

Бинарное отношение ф на множестве X — это множество, элементами которого являются упорядоченные пары элементов их на X, при этом если это множество содержит пару е ф, то вместо такой записи часто просто пишут х' ух” или

х*>хх"1.

Примеры бинарных отношений.

• 1. Пусть X — одно из числовых множеств, например, X — множество натуральных, X — целых, (2 — рациональных или 9? — вещественных чисел. Определим отношение ф на X следующим образом: если х х” е X, то х' ух” тогда и только тогда, когдах' < х”, т.е. когда числох" не превосходит числом". Это бинарное отношение называется стандартным отношением порядка на множестве X. Еще на этом же множестве X можно определить другое бинарное отношение ф следующим правилом: если х', х” е X, то х'ух” тогда и только тогда, когда х' < х”, т.е. когда число х' строго меньше числа х”. Такое бинарное отношение принято называть отношением строгого порядка на множестве X.
• 2. Пусть X — произвольное множество. Рассмотрим множество всех его подмножеств и введем на нем бинарное отношение ф следующим образом: если подмножества А, В а X, то А у В тогда и только тогда, когда А с В, т.е. когда подмножество А является подмножеством множества В. Это бинарное отношение называется отношением включения на множестве всех подмножеств множества X.
• 3. Пусть X — множество целых чисел иш - фиксированное целое число, больше 1. Определим отношение ф на X следующим образом: если х’, х” е X, то х' ух” тогда и только тогда, когда разность этих целых чисел х' - х” делится в множестве целых чисел X на т без остатка. В этом случае обычно говорят, что эти целые числа х х” е X сравнимы между собой по модуля числа т и записывают в виде х' = х”(то(1т). Это бинарное отношение называется отношением сравнения по модулю т на множестве целых чисел X.
• 4. Пусть Х= 9?т — т-мерное векторное пространство над полем вещественных чисел и заданы ш-мерные векторы а = (я1? а2,..., ат)у Ъ = (6Р й2,..., Ьт) е 9?,и.

Определим важные для дальнейшего материала учебника следующие четыре бинарные отношения >, >, >, ф на 9?т:

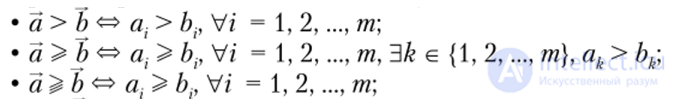
• а у Ь, если выполнено хотя бы одно из следующих условий:

Эти бинарные отношения, заданные на векторном пространстве 9?от, соответственно называются:

1 Верников Б. М. Бинарные отношения [Электронный ресурс], и И Б: http://kadm.imkn.urfu.ru/ filesZalggeom02.pdf (дата обращения: 04.08.2015).

• • > — строгого порядка (по всем координатам вектора);
• • > — строгого порядка {хотя бы по одной из координат вектора);
• • > — не строгого порядка;
• • (р — лексикографическим порядком.

Название последнего отношения объясняется тем, что именно в таком лексикографическом порядке происходит запись всех слов русского языка в любом словаре .

Выделим несколько важных видов бинарных отношений.

Определение

Пусть на произвольном множестве X задано бинарное отношение ф, тогда мы будем его называть:

рефлексивным, если для любого х е X выполняется .гср.г; иррефлексивным, если для любого х е X не выполняется х<рх; симметричным, если для любых х', х" е X из того, что х'ерх", следует, что выполнено х"(рх';

антисимметричным, если для любых х х" е X из того, что х' (рх" и х" ерт', следует, что это один и тот же элемент в множестве X, т.е. х' = х" е X; асимметричным, если для любых х х" е X из того, что выполняется х' (рх", всегда следует, что никогда не может выполняться соотношение х" (рх' транзитивным, если для любых х', х"' е X из того, что х' ф.т" и х" фд:"', сле

дует, что.г'ф.г'";

слабо связным, если для любых .г', д:" выполняется либо х' (рх", ли

бо х"(рх'.

При этом, если бинарное отношение является одновременно рефлексивным, симметричным и транзитивным, тогда его называют отношением эквивалентности (;или безразличия).

Нетрудно проверить, что приведенные выше примеры бинарных отношений обладают, например, следующими свойствами:

• • слабо связными отношениями будут только стандартное отношение порядка (<) и отношение строгого порядка (<), заданные на множестве натуральных, целых, рациональных или вещественных чисел, а также отношение ф — лексикографического порядка, заданное на векторном пространстве 9?от;
• • транзитивными отношениями будут все восемь отношений, которые приведены в вышеперечисленных примерах;
• • симметричным отношением будет только одно отношение — отношение сравнения по модулю т на множестве целых чисел;
• • рефлексивными отношениями будут только стандартное отношение порядка (<), заданное на множестве натуральных, целых, рациональных или вещественных чисел, отношение включения (с), заданное на множестве всех подмножеств множества X, и отношение сравнения по модулю т на множестве целых чисел и отношение (>) — не строгого порядка, заданное на векторном пространстве 91'";
• • отношением эквивалентности {или безразличия) будет только одно отношение порядка — отношение сравнения по модулю т на множестве целых чисел.

Обратите внимание!

При рассмотрении любой многокритериальной ЗПР с множеством допустимых решений X и заданным на нем отношением строгого предпочтения >х это отношение всегда будет бинарным отношением на множестве X, которое является асимметричным и иррефлексивным.

При этом векторный критерий /= (/,,/2, X —* 9?т позволяет ввести соответствующее отношение предпочтения на множестве возможных оценок Y = = Im(/) cz 9?w следующим образом: х', х" е X: х' >х х" => у' = /(д:') >у у” = =f(x") е Yа 9?"', что позволяет более наглядно производить анализ предпочтений ЛПР не только в множестве допустимых решений X, но и сравнение векторов в критериальном пространстве 9?"'.

Важно, что если векторный критерий / является биекцией, то верно и обратное утверждение. Об этом говорит сайт https://intellect.icu . Именно, если, например, в критериальном пространстве 9?т мы выбираем отношение > строгого порядка хотя бы по одной из координат вектора, то это правило, в свою очередь, задает (индуцирует) на множестве допустимых решений X свое отношение строгого предпочтения следующим образом: если у' = /(*'), у" = /(:г") е Yа 9Г': у' > у” => х' >хх' что позволяет более наглядно и значительно проще обосновывать и осуществлять выбор оптимального (или наилучшего) с точки зрения ЛПР управленческого решения.

Более подробно взаимосвязь между отношением строгого предпочтения >х в ЗПР и векторными оценками в критериальном пространстве будет рассматриваться в гл. 9 при рассмотрении аксиом Парето.

Обратите внимание!

Общая постановка ЗПР при многих критериях в условиях определенности включает в себя:

• 1) нахождение множества допустимых решений Х
• 2) построение векторного критерия

• 3) описание отношения предпочтений ЛИР >х, заданного на множестве Х
• 4) нахождение подмножества выбираемых решений С(Х) с Хна основе отношения предпочтений ЛИР >х и векторного критерия /, которые и отражают предпочтения и пели субъекта управления.

Заметим, что данное описание общей постановки ЗПР при многих критериях дано в терминах нахождения множества оптимальных (или наилучших) с точки зрения целей ЛПР управленческого решения из множества допустимых решений X. В то же время наличие векторного критерия /, как это было показано выше, позволяет достаточно легко переформулировать нашу многокритериальную ЗПР в терминах векторов из критериального пространства 9?'" и множества векторных оценок У = 1т(/) с 9?т1.

Обратите внимание!

Математическая модель решений ЗПР, которая учитывает состояние внешней среды и задание критериальных (оценочных) функций, в более общем виде будет рассмотрена ниже в заключительной части этого параграфа.

Математическая модель принятия решений в многокритериальной ЗПР с учетом состояния внешней среды представляет собой формализацию соответствующей задачи принятия решений (ЗПР). В силу важности этого материала остановимся более подробно на ключевых этапах построения такой модели. Поиск решения начинается с перечисления возможных (допустимых) вариантов решений и их исходов, затем производится оценка и анализ каждого исхода. Для построения модели необходимо задать следующие три множества:

X — множество допустимых альтернатив (действий, управленческих решений, стратегий, вариантов, планов, из которых ЛПР может выбрать только один элемент);

5 — множество возможных состояний среды, из которых может реализовываться одно и только одно состояние;

Я — множество возможных результатов или исходов, полученных в результате реализации принятого управленческого решения (событий, имеющих, если не задано ничего дополнительного, совершенно произвольную структуру).

Всегда предполагается, что множество X содержит не менее двух альтернатив — иначе надобность в принятии решения отпадает.

Лицо, принимающее решение, выбирает одну из возможных альтернатив, при этом каждый исход (результат) зависит как от выбранной альтернативы, так и от состояния среды. Таким образом, каждый исход г е Я мож-

но представить как результат действия некоторого отображения Е из прямого произведения двух множеств (т.е. из множества упорядоченных пар элементов двух множеств) в множество возможных результатов (исходов) /?, т.е.

Определение

Отображение Е: Ь'хХ- ? Я называется функцией реализации или функцией выбора управленческого решения или действия.

Обратите внимание!

Набор объектов (5, X, R, Е> составляет реализационную структуру задачи принятия решения.

реализации содержит не один элемент. В общем случае критерий всегда подразумевает тот или иной анализ некоторого заданного множества. Элементы анализируемого множества в контексте критериального подхода принято называть альтернативами, и это может создать определенную путаницу с понятием «альтернатива», как элемент множества X в задаче принятия решений. Чтобы избежать этой путаницы мы (по мере возможностей), в зависимости от контекста, будем употреблять словосочетания соответственно: «альтернативы критерия» и «альтернативы управленческих решений», «альтернативы действий», «альтернативы стратегий». Отметим, что изначально на множестве альтернатив критерия не предполагается предварительного задания никакой структуры.

Определение

Критерием, заданным на множестве, называемом множеством альтернатив критерия, мы называем пару: признак и правило, позволяющую разбить заданное множество (но данному признаку с помощью заданного правила) на два непересекающихся и взаимно дополняемых подмножества, которым присваиваются два различных логических значения: {TRUE, FALSE} или соответствующие им индикаторные значения {1,0}.

Критерий всегда должен сопровождаться критериальной (оценочной) функцией, на основании которой реализуется правило, производящее разбиение. Критериальная функция всегда должна действовать из критериального множества в некоторое линейно упорядоченное множество. В случае, когда это линейно упорядоченное множество представляет собой подмножество вещественных чисел 9?, принято говорить об оценочной функции.

Замечание. В философии особо выделяют критерии истинности знания. Различают логические и эмпирические критерии истинности. Так говорят: «Практика — критерий истинности», подразумевая эмпирические критерии. Вместе с эмпирическими критериями рассматриваются и теоретические критерии. Критерий истинности математической теоремы - строгость ее доказательства.

В контексте нашего введенного формализма, т.е. реализационной структуры (5, Ху R, F)y и порядка важности решаемых задач множеством альтернатив критерия в первую очередь будет являться элемент структуры (X) - множество альтернатив управленческих решений, а во вторую очередь (S) - множество состояний среды, а если точнее — то множество вероятностных распределений на множестве состояний среды.

К эмпирическим критериям относятся статистические критерии проверки гипотез. Как раз в этом случае множеством альтернатив критерия является множество вероятностных распределений, заданных на множестве состояний среды.

Действие критерия проявляется уже на стадии формирования реализационной структуры. Так, говоря о «допустимых» стратегиях (альтернативах), мы по некоторому «стоящему за кадром» критерию отсеиваем все «недопустимые» стратегии. Для того, чтобы оценить «правильность» выбранного действия или принятого решения, ЛПР необходимо иметь критерий сравнения управленческих решений. Так как само по себе, в отрыве от результата, УР ничего не значит, и решения сравниваются по результатам (исходам), к которым они приводят, то возникает необходимость иметь критерий

(критерии) сравнения результатов. В этом случае множеством альтернатив критерия становится Я — множество результатов (исходов). Для такого критерия признаком будет предпочтительность (или приемлемость) того или иного результата, а правилом — следующее введенное отношение строгого предпочтения на множестве Я.

Строгое предпочтение г1 > г2 означает, что исход г, предпочтительней, чем г2, и нестрогое предпочтение г{ > г2 означает, исход г1 не менее предпочтителен, чем исход г2.

В случае, если ЛПР может оценить эффективность (равнозначные по смыслу термины: «полезность», «ценность») каждого исхода г е Я некоторым числом ф(г) из множества вещественных чисел 9?, то задается оценочная структура задачи принятия решений в виде пары (Я, (р), где функция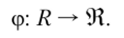

Определение

Функция (р называется оценочной (критериальной) функцией предпочтения, заданной на множестве Я всех возможных результатов (исходов), которые можно получить при реализации управленческих решений из заданного множества X — допустимых решений.

После того, как мы ввели понятие критериальной функции, на ее основе зададим операцию сравнения двух результатов гр г2 е Я по следующему признаку предпочтения

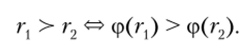
Говорят, что (оценочная) функция ф порождает (частичное) отношение порядка на множестве реализаций Я. Так как критериальная функция позволяет вычислять численное значение отношения предпочтения, то очевидным образом, на основе отношения строгого порядка на множестве вещественных чисел 9?, возникает правило, дающее предпочтения по данному критерию и, как следствие, позволяющее разбивать (на два подмножества, как требуется при разбиении в определении критерия, но и не только так) множество результатов в соответствии с признаком предпочтения.

Замечание. Отметим, что множество значений оценочной функции может влиять на формирование самой реализационной структуры ЗПР. Может так оказаться, что множество допустимых действий (альтернатив) X не дает ни единого приемлемого значения оценочной функции. Так, например, вы заходите в кафе пообедать и убеждаетесь, что за ваш бюджет вы не можете получить приемлемого полноценного обеда.

Пример: задания оценочной структуры ЗПР. Один из самых простых, но при этом основных способов задания оценочной структуры задачи принятия решений заключается просто в разбиении множества исходов Я на два непересекающихся подмножества: Я = Я* и Я{ Я* П Я0 = 0, где Я° — класс «плохих» (неприемлемых, недопустимых) исходов, а Я* — класс «хороших» (приемлемых, допустимых) исходов. Оценочная функция ф здесь изначально не задается, а порождается собственно разбиением и представляет собой индикаторную функцию, заданную на множествах разбиения: О, если «плохо», и 1, если «хорошо». Также здесь оценочной функции можно приписать и логические значения {TRUE, FALSE}.В этом случае признаком критерия для сравнения двух исходов будет следующее соотношение

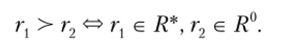
Правило же критерия, дающее здесь разбиение критериального множества альтернатив, реализуется заранее, «за кадром», на основе, возможно, индивидуального представления ЛГ1Р о «хорошем» и «плохом» исходе. При этом заметим, что данной модели оценочной структуры исходы, принадлежащие одному из множеств, между собой предполагаются несравнимыми (равноценными или эквивалентными с точки зрения ЛПР).

Пример: следующий способ построения оценочной структуры с логической оценочной функцией использует некоторую «начальную» оценочную функцию ф, реализуемую уже «в кадре». Разбиение множества исходов R на два класса здесь осуществляется следующим способом, который представляет собой пример применения критерия, где множеством альтернатив критерия будет множество результатов, а критериальной функцией будет функция ф. Следует задать некоторое пороговое (критическое) значение с* е 5?К для функции ф. Тогда получим следующее разбиение множества R = = R° U R* на два непересекающихся подмножества

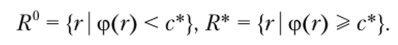
Здесь значением признака сравнения г будет значение, которое приняла ф(г), а правилом, порождающим разбиение R = R° U /?*, будет правило сравнения с критическим значением с* е 9?.

Более общим случаем будет выбор некоторого (открытого) подмножества вещественных чисел Х0 а 9?, которое принято называть критическим, задающего разбиение множества исходов следующим образом

Заметим, что критерии такого типа применяются, например, в задачах проверки статистических гипотез при построении критериев согласия.

Пример: компания опубликовала объявление о приеме на работу биз- нес-информатиков в возрасте от 20 до 50 лет. Тогда критическим множеством «хороших» исходов для претендентов будет интервал их возраста — 120, 501-

Логические значения множеств {R°, R*} могут меняться местами в зависимости от предпочтений.

Определение

Целевой функцией / заданной ЗПР будем называть последовательное применение функции реализации и оценочной функции (композицию, суперпозицию соответствующих функций)

Вещественное число /($, х) е 9? отражает полезность (ценность, эффективность) того исхода, который получается в ситуации, когда ЛПР выбирает управленческую альтернативу х € Х} а среда принимает некоторое состояние 5 е 5. Заметим, что в экономике (да и политике) нередко можно столкнуться с ситуацией, когда выбор полезности влияет на состояние среды. «Полезность» пушнины, например, приводит к перманентному уменьшению соответствующих животных в лесах и, в лучшем случае, — к появлению ферм по их искусственному выращиванию. Полезность рождает спрос -» —*• спрос рождает предложение —*? предложение меняет состояние среды.

В случае, когда Л ПР стремится к увеличению значения функции/, выбирая управленческую альтернативу, то говорят, что / показывает ценность, эффективность или выигрыш. В противном случае, при стремлении ЛПР к уменьшению значений /эта выражает потери, проигрыш, ущерб, риски.

Заметим, что оценочная структура ЗПР носит субъективный характер: оценивание исходов производится сточки зрения принимающего решение. Наиболее распространенным является задание оценочной структуры в виде оценочной функции ф или целевой функции /.

В зависимости от информации, которую имеет при принятии решения ЛПР относительно состояния внешней среды, различают несколько основных типов задач принятия решения. Приведем их классификацию по этому признаку.

• Ногин В. Д. Указ. соч.
• Формальная модель задачи принятия решений при многих критерияхв условиях определенности внешней среды. При решении любой многокритериальной ЗПР в качестве исходной информации обычно принимаетсяописание проблемной ситуации состояния управляемой системы и наличиересурсов, в том числе и временных, которые выделены для решения даннойзадачи. В процессе решения ЗПР: формулируются цели и критерии выбораальтернатив из множества допустимых решений X для перевода управляемойсистемы из неудовлетворительного состояния в оптимальное (или наилучшее)с точки зрения целей ЛПР; уточняются состояние внешней среды и граничные условия; определяется множество допустимых решений X; с учетом целей и предпочтений ЛПР строится на множестве X векторный критерий /и отношение предпочтений ЛПР >х; обосновывается и производится выбороптимального (наилучшего) с точки зрения целей ЛПР управленческогорешения. Вместе с тем с математической точки зрения ключевыми компонентами при общей постановке ЗПР при многих критериях являются:
• нахождение множества допустимых решений Х
• построение векторного критерия
• описание отношения предпочтений ЛПР >х, заданного на множестве X;
• нахождение подмножества выбираемых решений С(Х) а X на основеотношения предпочтений ЛПР >х и векторного критерия /, которые и отражают предпочтения и цели субъекта управления. Именно знание множества допустимых решений X и заданных на немвекторного критерия / и отношения предпочтений ЛПР >х позволяет экспертам без участия ЛПР произвести обоснованный выбор оптимального(или наилучшего) с точки зрения целей ЛПР управленческого решения.
• Ногин В. Д. Указ. соч.
• Заметим, что функций выбора может быть несколько, но мы пока ограничиваемся рассмотрением одной. Пример: рассмотрение одной из функции выбора. Пусть некто, например, студент Петр, имеет мобильный телефон. Ему необходимо внести абонентскую оплату. Множество альтернатив можно строить разными способами. В самом простом случае, соответствующем логическим {TRUE, FALSE},Петр может принимать решение вносить или не вносить деньги за телефон.В этом случае множество альтернатив будет состоять из двух элементов:Х= {0,1} (иметь «бинарную», «булеву» структуру). В несколько более общемслучае, когда Петр выбирает из трех следующих альтернатив: не вноситьоплату, внести не более 100 руб. или внести более 100 руб., множество альтернатив X очевидно превратится в множество, состоящее из трех элементов. В случае, когда рассматривает варианты внести любую сумму в пределах от 0 до 1000 руб., то множество X будет представлять собой интервалчисловой оси. Отметим, что шаг дискретизации этого интервала, будет равен шагу дискретизации платежной системы: 1 коп., 10 коп., 1 руб., 10 руб.,50 руб., 100 руб. В подобных вопросах современная литература по вычислительным финансам рекомендует использовать непрерывную денежнуюшкалу — в этом случае множество альтернатив представит собой непрерывный интервал [0, 1000]. Состоянием среды s е S будет сумма на счете телефона на некоторую конкретную дату — дату принятия решения (управленческого решения по управлению денежным счетом телефона). Принявопределенное решение и выбрав какую-либо альтернативу, Петр начинаетпользоваться телефоном или не имеет такой возможности. Множество исходов (результатов) будет состоять из двух элементов R = {rv г2}, где г, == {телефон отключен}, г2 = {телефон не отключен}. Теория принятия решений неотделима от понятия критерия. Уточнимпонятие критерия, заданного в зависимости от контекста, на исходных множествах (S, X, R, F): а) на множестве X — альтернатив, действий в задачепринятия решений; б) на множестве S — состояний среды, в первую очередь,на множестве гипотез о состоянии среды; в) на множестве R — результатов;г) на множестве F — функций реализации управляющего решения. Еслирассматривается многокритериальная ЗПР, то и множество функции F ее

Исследование, описанное в статье про Бинарные отношения., подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Бинарные отношения. и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений