4.3 Принятие решений с использованием аппарата теории нечетких множеств

Привет, сегодня поговорим про принятие решений с использованием аппарата теории нечетких множеств, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое принятие решений с использованием аппарата теории нечетких множеств , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Алгоритм Мамдани используется для многокритериальной оценки объектов по набору критериев [15]. Входными данными для алгоритма являются описание и значения нечетких переменных, правила вывода. Результатом работы алгоритма являются четкие значения выходных переменных.

На первом этапе определяется набор критериев k_1, k₂, …, k_v для оценки объектов, им в соответствие ставятся нечеткие переменные.

Нечеткие переменные представляют собой тройку <a, X, A>, где a - имя переменной, X - область определения a, A – нечеткое множество наX, которое может быть охарактеризовано набором функций принадлежности  m_A(x). Множества X и A определяются конкретным критерием. Например, если в качестве критерия выступает «месторасположение фирмы», то ему будет соответствовать одноименная нечеткая переменная, множество значений которой можно описать тройкой «удобное», «не очень удобное», «неудобное».  Каждому значению будет соответствовать своя функция принадлежности.

Правила представляют собой конструкции вида

«если <сложное условие>, то <список выходов>», где

<сложное условие>             :-     or(<список условий>) |

                                                     and(<список условий>) |

                                                     <условие>

 

<список условий>                :-     (<условие>)[<список условий>]

<условие>                            :-     <имя входной нечеткой переменной>

                                                     <значение входной нечеткой переменной>

<список выходов>               :-     (<значение выхода>)[<список выходов>]

 

<значение выхода>             :-     <имя выходной нечеткой переменной>

                                                     <значение выходной нечеткой переменной>

 

Рассмотрим работу алгоритма Мамдани на примере (рис.4.5). Пусть база знаний состоит из двух правил:

П1: если х есть А1 и у есть В1, тогда z есть С1,

П2: если х есть А2 и у есть B2, тогда z есть С2,

где х и у — имена входных переменных, z - имя переменной вывода, A1, A2, B1, B2, C1, C2 — некоторые заданные функции принадлежности, при этом четкое значение z₀  необходимо определить на основе приведенной информации и четких значений x₀ и y₀.

 

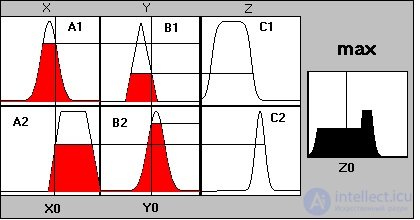
Рис. 4.5. Основные этапы работы алгоритма Мамдани

Алгоритм состоит из 4 этапов:

1.    Введение нечеткости: находятся степени истинности для предпосылок каждого правила: A1(x₀), A2(x₀), B1(y₀), B2(y₀). Например, A1(x₀) – это значение функции принадлежности A1 переменной x в точке x₀.

2.    Нечеткий вывод: находятся уровни «отсечения» для предпосылок каждого из правил (при этом для логической операции «и» используется операция min, для логической операции «или» используется операция max).

                                               a1 = A1(x₀) Ù B1(y₀)

                                               a2 = A2(x₀) Ù B2(y₀)

Затем находятся усеченные функции принадлежности для выходной переменной.

                                               С'₁ = (a1 Ù C1(z))

                                           С'₂ = (a2 Ù C2(z))

3.    Композиция: с использованием операции max производится объединение найденных усеченных функций, что приводит к получению итоговой функции принадлежности для выходной переменной.

μ_S(z) = C(z) = С'₁Ú С'₂ = (a1 Ù C1(z)) Ú (a 2Ù C2(z))=

= (A1(x₀) Ù B1(y₀) Ù C1(z)) Ú (A2(x₀) Ù B2(y₀) Ù C2(z))

4.    Дефаззификация: находится четкое значение выходной переменной z₀ (например, центроидным методом (как центр тяжести для кривой μ_S(z)):

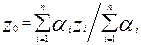                             - для дискретного варианта.

 

Пример построения рейтинга компьютерных фирм на основе метода Мамдани

В качестве критериев для оценки объектов в данном случае выступают «качество обслуживания клиентов» и «месторасположение фирмы». Об этом говорит сайт https://intellect.icu . Оба критерия измеряются в пятибалльной шкале, то есть эксперт в качестве значения критерия может выбрать любое целое число в интервале от 0 до 5. Поставим критериям в соответствие нечеткие переменные (Таблица 4.10).

Таблица 4.10

Параметры нечеткой переменной	Имя нечеткой переменной a
	«Качество обслуживания клиентов» (КО)	«Месторасположение фирмы» (МФ)
Область определения X	[0,5]	[0,5]
Значения нечеткой переменной	«отличное», «приемлемое», «плохое»	«удобное», «не очень удобное», «неудобное»
Функции принадлежности  для значений нечеткой переменной

 

В качестве выходной переменной будет выступать «рейтинг объекта» (Таблица 4.11).

Таблица 4.11

 

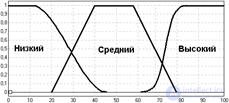Для простоты вычислений пусть система правил вывода состоит из 3 правил.

П1: Если КО отличное (А1) и МФ неудобное (В1), то рейтинг средний (C1).

П2: Если КО приемлемое (А2) и МФ не очень удобное (В2), то рейтинг низкий (C2).

П3: Если КО плохое (А3) и МФ удобное (В3), то рейтинг низкий (C3).

Исходные данные представим в виде таблицы 4.12

Таблица 4.12

 

Рассмотрим основные этапы работы алгоритма.

Этап 1. Введение нечеткости

Найдем степени истинности для предпосылок каждого правила.

Таблица 4.13

 

Этап 2. Нечеткий вывод

Найдем уровни «отсечения» для предпосылок каждого из правил.

Таблица 4.14

№ фирмы	П1	П2	П3
1	a1=min(0.5,0.35)=0.35	a2=min(0,0)=0	a3=min(0,0)=0
2	a1=min(0,0)=0	a2=min(1,0.65)=0.65	a3=min(0,0)=0
3	a1=min(0,0)=0	a2=min(0,0)=0	a3=min(0.5,0.3)=0.3

 

Найдем усеченные функции принадлежности для выходной переменной.

Таблица 4.15

№ фирмы	П1	П2	П3
1	С'1=a1 Ù C1 (0.35)	С'2=a2 Ù C2 (0)	С'3=a3 ÙC3 (0)
2	С'1=a1 Ù C1 (0)	С'2=a2 Ù C (0.65)	С'3=a3 Ù C3 (0)
3	С'1=a1 Ù C1 (0)	С'2=a2 ÙC2 (0)	С'3= a3 Ù C3 (0.3)

 

Этап 3 и 4. Композиция и дефаззификация

Таблица 4.16

Таким образом, в результате работы алгоритма мы имеем набор четких значений выходной переменной «рейтинг» в выбранной нами шкале измерений значений переменной: z₁, z₂, …, z_m, где m – число фирм. Упорядочив полученные значения по убыванию, получим рейтинг фирм P.

Надеюсь, эта статья об увлекательном мире принятие решений с использованием аппарата теории нечетких множеств, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое принятие решений с использованием аппарата теории нечетких множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений

Из статьи мы узнали кратко, но содержательно про принятие решений с использованием аппарата теории нечетких множеств