Привет, сегодня поговорим про групповые методы принятия решений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое групповые методы принятия решений , настоятельно рекомендую прочитать все из категории Теория принятия решений.

5.1     Постановка задачи

Дано:

   a₁, a₂, …, a_n – альтернативы, n – количество альтернатив,

   P₁, P₂, … P_m – индивидуальные ранжирования альтернатив экспертами, m – количество экспертов.

Ранжирования имеют вид 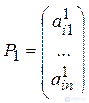 , где

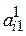  – альтернатива, стоящая на первом месте в ранжировании P₁,

  – альтернатива, стоящая на n-ом месте в ранжировании P₁.

Альтернатива 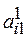  имеет ранг 1, альтернатива 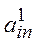имеет ранг n.

Требуется найти: итоговое ранжирование P*, учитывающее мнение всех экспертов.

5.2    Правило большинства

Согласно правилу большинства подсчитывается число экспертов, отдавших предпочтение каждой из альтернатив, и наилучшей объявляется альтернатива, которую назвали лучшей большинство экспертов. Пусть рассматриваются 5 альтернатив. Их ранжирования, соответствующие мнению 10 экспертов, представлены в табл. 5.1:

Таблица 5.1

Пример ранжирования альтернатив экспертами

В данном случае, по правилу большинства лучшей окажется альтернатива A1, так как ее назвали лучшей 3 эксперта (для остальных альтернатив это число меньше или равно 2). Однако эту же альтернативу признали худшей 7 из 10 экспертов. Так что признание альтернативыA1 лучшей весьма спорно. Для устранения подобных недостатков вводят дополнительные требования. Например, лучшей может стать только та альтернатива, которую считают лучшей не менее половины экспертов. При таких условиях лучшей альтернативы вообще может не оказаться.

5.3    Принцип Кондорсе

Кондорсе был предложен следующий случай определения лучшей альтернативы. Каждый эксперт ранжирует альтернативы по предпочтениям. На основании полученных ранжирований для каждой пары альтернатив A_i и A_j подсчитывается S_ij – число экспертов, считающихA_i более предпочтительной, чем A_j. Если S_ij >S_ji, то альтернатива A_i признается боле предпочтительной, чем A_j. Лучшей альтернативой объявляется A_i, если S_ij >S_ji для всех i ≠ j. В данном случае альтернативой Кондорсе является альтернатива A2. Однако при использовании принципа Кондорсе может возникнуть парадокс, являющийся следствием нетранзитивности коллективных отношений. Если три эксперта проранжировали альтернативы A1, A2, A3 следующим образом:

A1      A3      A2

A2      A1      A3

A3      A2      A1

то S₁₂>S₂₁, S₂₃>S₃₂, S₃₁>S₁₃. Альтернативы Кондорсе в данном случае не существует.

5.4    Метод Борда

В основе метода Борда лежит упорядочивание альтернатив на основе сумм рангов, назначенных альтернативам экспертами [6, с. 62]. Альтернативам, проранжированным экспертами, ставится в соответствие число: последней по предпочтению – 0, предпоследней – 1 и т.д. Метод состоит из 2 этапов:

1.    на первом этапе для каждого объекта с номером k определяется величина S_k, равная сумме рангов, присвоенных объекту всеми экспертами:

;

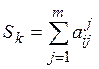2.    на втором этапе определяется ранг объекта – чем больше величина S_k, тем выше место альтернативы в искомом ранжировании.

Пример построения итогового ранжирования с помощью метода Борда

Пусть имеются альтернативы a₁, a₂, a₃, a₄ и ранжирования этих альтернатив экспертами (табл. 5.2). Требуется найти итоговое ранжирование.

Таблица 5.2

Ранжирования критериев экспертами

Обозначим полученные на основе ранжирований альтернатив экспертами ранги R₁, R₂, R₃, R₄.Процесс построения итогового ранжирования с помощью метода Борда представлен в табл. Об этом говорит сайт https://intellect.icu . 5.3.

Таблица 5.3

Построение итогового ранжирования

5.5      Метод поиска медианы Кемени

Метод поиска медианы Кемени позволяет найти такое итоговое ранжирование P, суммарное расстояние от которого до всех заданных ранжирований минимальное:

,

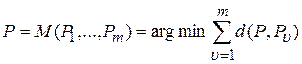где m – количество экспертов, P₁, …, P_m – ранжирования, d(P,P_u) – расстояние между ранжированиями [6, с. 73].

Таким образом, для поиска медианы необходимо ввести понятие расстояния между ранжированиями. Оно определяется с помощьюматриц отношений 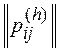, ,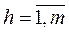 , 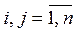n – количество альтернатив.

r_i, r_j – ранги i-той и j-той альтернатив в ранжировании h-ого эксперта. Отметим, что ранги альтернатив сравниваются наоборот, то есть рангr_i=1>r_j=2 (ранг 1 больше ранга 2) и r_i=5<r_j=3 (ранг 5 меньше ранга 3).

Расстояние от произвольного ранжирования P, которому соответствует матрица , до всех ранжирований P₁, P₂, …, P_m, которым соответствуют матрицы парных отношений 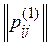, …,  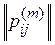определяется по формуле:

.

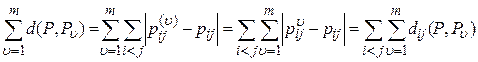Для нахождения медианы Кемени вводится матрица потерь , .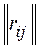

,

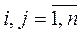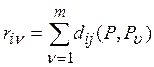где P – ранжирование, элемент матрицы отношений p_ij которого равен 1.

При этом задача поиска медианы Кемени для ранжирований формулируется как задача отыскания такого упорядочения альтернатив, а следовательно, строк и столбцов матрицы потерь, чтобы сумма ее элементов, расположенных над диагональю, была минимальна.

Эвристический алгоритм поиска медианы Кемени

Пусть для исходных ранжирований матрица потерь определена. Процесс поиска итогового ранжирования состоит из 2 этапов.

На первом этапе строится предварительное ранжирование P_I.

1-я итерация. Подсчитаем суммы элементов строк матрицы потерь:

.

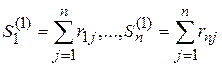Найдем минимальную из них .

Альтернативу а_i1, ставим на первое место в искомом ранжировании. Вычеркивая в 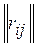 строку и столбец с номером i₁, получаем матрицу , множество индексов строк и столбцов которой соответственно I⁽¹⁾=J⁽¹⁾={1,…,n}\ I₁.

k-я итерация. В матрице потерь 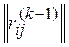 подсчитаем суммы элементов строк:

.

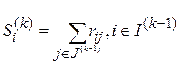Найдем минимальную из них:

.

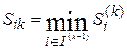Альтернативу а_ik, ставим на k-тое место в искомом упорядочении. Вычеркивая в 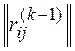 строку и столбец с номером i_k, получаем матрицу 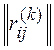, множество индексов строк и столбцов которой соответственно I^(k)=J^(k)={1,…,n}\ {i₁, …,i_k}.

Алгоритм завершается после n-й итерации (I^(k)=J^(k) и равны пустому множеству). Искомое упорядочение

На втором этапе из найденного ранжирования P_I получают итоговое ранжирование P_II, при этом процесс перехода от ранжирования P_I к ранжированию P_II происходит следующим образом: для элементов ранжирования P_I последовательно проверяем справедливость соотношений (1)

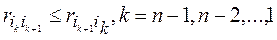                  (5.1)

Как только для некоторого k оно нарушено, альтернативы a_ik и a_ik+1 в ранжировании меняем местами, а соотношение (5.1) проверяем, начиная с альтернативы, непосредственно предшествующей альтернативе, подвергшейся перестановке. После конечного числа шагов будет получено ранжирование P_II.

Пример построения итогового ранжирования с помощью метода поиска медианы Кемени

Рассмотрим процесс построения итогового ранжирования на примере, рассмотренном ранее (исходные данные представлены в табл. 5.2).

1.    Построим матрицы отношений для ранжирований экспертов:

	0	-1	-1	-1		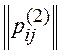0	-1	-1	-1
	1	0	-1	1		1	0	1	1
	1	1	0	1		1	-1	0	1
	1	-1	-1	0		1	-1	-1	0
	0	1	1	1		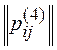0	0	-1	-1
	-1	0	-1	-1		0	0	-1	-1
	-1	1	0	0		1	1	0	-1
	-1	1	0	0		1	1	1	0

Например, p₁₂⁽¹⁾=-1, так как r₁<r₂ (r₁=3, r₂=1), p₃₄⁽²⁾=0, так как r₃=r₄ (r₃=2, r₄=2).

2.    Матрица потерь имеет следующий вид:

Например, r₁₂=d₁₂(P₁,P₃)+d₁₂(P₂,P₃)+d₁₂(P₄,P₃), так как P₃ – ранжирование, элемент матрицы отношений которого p₁₂⁽³⁾=1. Тогдаr₁₂=|p₁₂⁽³⁾-p₁₂⁽¹⁾|+|p₁₂⁽²⁾-p₁₂⁽³⁾|+|p₁₂⁽³⁾-p₁₂⁽⁴⁾|=|1-(-1)|+ |1-(-1)|+ |1-0|=5.

3.    Найдем предварительное ранжирование P_I (первый этап).

1-я итерация. Подсчитаем

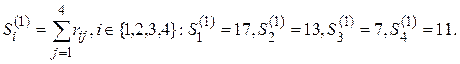
Минимум достигается на S₃⁽¹⁾. На первое место в ранжировании P_I помещается альтернатива a₃, и она из дальнейших рассмотрений исключается.

2-я итерация. Подсчитаем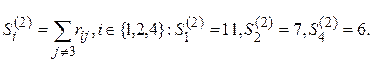 

Минимум достигается на S₄⁽²⁾. На второе место в ранжировании P_I помещается альтернатива a₄, и она из дальнейших рассмотрений исключается.

3-я итерация. Подсчитаем 

Минимум достигается на S₂⁽³⁾. На третье место в ранжировании P_I помещается альтернатива a₂, и она из дальнейших рассмотрений исключается. Таким образом, ранжирование P_I имеет следующий вид:

4.    Найдем ранжирование Р_II (второй этап).

Итак, i₁=3, i₂=4, i₃=2, i₄=1. Сравниваем 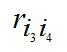      и 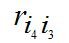 или r₂₁ и r₁₂, Так как r₂₁≤r₁₂ (3≤5), то альтернативы не меняем местами, переходим к сравнению r₄₂ и r₂₄. Так как r₄₂≤r₂₄ (4≤4), то переходим к сравнению r₃₄ и r₄₃.  Поскольку r₃₄<r₄₃ (3≤5), то найденное ранжирование

и является ранжированием Р_II, для которого соотношения (5.1) выполнены.

Итоговые ранжирования альтернатив по методу Борда и методу поиска медианы Кемени представлены в табл. 5.5.

Таблица 5.5

Результаты построения итогового ранжирования с помощью метода Борда и метода поиска медианы Кемени

Результаты работы описанных выше методов иногда могут различаться достаточно сильно. Метод Борда дает результаты, которые интуитивно понятны, так как в его основе лежит идея усреднения оценок. Что касается метода поиска медианы Кемени, то он, наоборот, может давать непредвиденные результаты. Для получения итогового ранжирования в методе используется специально оценка – расстояние между ранжированиями. А рассмотренный нами алгоритм получения итогового ранжирования основан на эвристике – предположении, что построенное таким образом итоговое ранжирование и будет наиболее близким к мнению всех экспертов с точки зрения введенной оценки.

Надеюсь, эта статья об увлекательном мире групповые методы принятия решений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое групповые методы принятия решений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений