Лекция
Привет, Вы узнаете о том , что такое МОДЕЛИРОВАНИЕ ПРЕДПОЧТЕНИЙ Математическая модель предпочтений в задачах принятия решений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое МОДЕЛИРОВАНИЕ ПРЕДПОЧТЕНИЙ Математическая модель предпочтений в задачах принятия решений , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Одной из главных составляющих задачи принятия решений является такое понятие, как предпочтение лица, принимающего решения.
Определение
Предпочтением ЛПР будем называть выраженное каким-либо образом его личное суждение о наличии или отсутствии преимущества одного из вариантов (альтернатив) выбора по отношению к другому варианту или ко всем остальным вариантам, либо в целом, либо по некоторым отдельным характеристикам .
Субъективность предпочтений выражается в том, что у каждого ЛГГР может быть своя система ценностей. Предпочтения могут быть описаны в явной форме или выявляться с помощью каких-либо правил или принципов, описанных с помощью логико-математических методов.
Пример: субъективности предпочтений. Директору некоторого предприятия необходимо выбрать подходящего кандидата на должность своего заместителя. Естественно, что выбор он будет делать исходя из своей собственной системы предпочтений. Для одного директора наиболее предпочтительными окажутся кандидаты, обладающие нестандартным мышлением, для другого — ответственные и исполнительные кандидаты, а для третьего — конформисты.
Обратите внимание!
Для решения ЗПР важно знать систему предпочтений ЛПР.
Таким образом, выявление наилучших вариантов из имеющегося набора для ЛПР производится на основе его представления о качестве этих вариантов. При этом представление о качестве этих вариантов характеризуется с помощью принципа оптимальности, математическим выражением которого является функция выбора .
Определение
Обозначим через X множество альтернатив задачи, из которых необходимо выбрать наиболее предпочтительные для ЛПР.
Обозначим через X множество наиболее предпочтительных вариантов для ЛПР, тогда Хявляется подмножеством множества X: Ха X.
Функцией выбора С называется правило, ставящее в соответствие множеству X его подмножество альтернатив X: С(Х) = X
Таким образом, принцип оптимальности задает понятие «наилучших» или наиболее предпочтительных для ЛПР альтернатив:
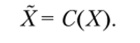
При этом возможно С(Х) = 0, что интерпретируется как отказ от выбора. Примерами такого отказа могут быть ситуации, когда покупатель не приобретает никакого товара в магазине или из группы студентов никто не был выбран для участия в олимпиаде.
Определение
|| Математической моделью предпочтений называется пара (X, С(Х))
Следует заметить, что не всякая функция, ставящая в соответствие некоторому множеству его подмножество, может интерпретироваться как функция выбора. Об этом говорит сайт https://intellect.icu . Необходимо наложить некоторые ограничения на производимый выбор. При этом нельзя однозначно выделить список ограничений или свойств такой функции, так как принципы выбора зависят от конкретной задачи принятия решений. Например, если какое-либо предприятие оказалось среди лучших в рейтинге предприятий своей страны, но не попало в число лучших в своей отрасти, то такой рейтинг кажется странным и по меньшей мере необоснованным. При этом вполне возможно, что среди учеников школы, получивших лучшие результаты итоговых экзаменов, могут оказаться те, кто не является победителем или призером олимпиад.
В зависимости от особенностей конкретной задачи на функцию выбора накладываются определенные ограничения. Перечислим характеристические свойства, которым может удовлетворять функция выбора.
1. Свойство наследования: если КсХ, то С(Х) П УсС(У).
Это свойство можно проиллюстрировать следующим примером. Если X — множество студентов экономического факультета, а У — студенты одной из групп этого факультета, то лучшие студенты экономического факультета, учащиеся в этой группе, будут среди лучших студентов этой группы.
2. Свойство согласия: если X = У и 7, то С(У) П С(Х) с С(Х).
Если, например, X — множество девушек, учащихся на экономическом факультете, то девушки, оказавшиеся в списке лучших студентов группы У, окажутся среди лучших студентов экономического факультета.
3. Свойство отбрасывания: если С(Х) сУсС,тоС(У) = С(Х).
Для описанного выше примера это свойство означает, что исключение из числа участников конкурса студентов, не являющихся лучшими, не меняет состава лучших студентов факультета.
4. Свойство строгого наследования: если У с X, У П С(Х) 0 или С(Х) = 0, то С(У) = УП С(Х) дляХ, У Ф 0.
Для описанного примера это свойство означает, что только лучшие студенты факультета войдут в списки лучших студентов групп этого факультета. Это свойство накладывает более жесткие требования, чем свойство наследования 1. Из выполнения свойства 4 следует выполнение свойства 1, однако из выполнения свойства 1 совсем не обязательно должно следовать соблюдение свойства 4.
Обратите внимание!
Несмотря па то, что перечисленные свойства кажутся вполне естественными, существуют практически интересные задачи, функции выбора которых не удовлетворяют ни одному из них.
Исследование, описанное в статье про МОДЕЛИРОВАНИЕ ПРЕДПОЧТЕНИЙ Математическая модель предпочтений в задачах принятия решений, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое МОДЕЛИРОВАНИЕ ПРЕДПОЧТЕНИЙ Математическая модель предпочтений в задачах принятия решений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений