Построение бинарных отношений предпочтения на множестве вероятностных распределений кратко

Привет, Вы узнаете о том , что такое Построение бинарных отношений предпочтения на множестве вероятностных распределений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Построение бинарных отношений предпочтения на множестве вероятностных распределений , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Для ЗПР в условиях вероятностной неопределенности множеством задания бинарных отношений предпочтения является множество всевозможных вещественных функций распределения Т (см. (7.1)), описанное в параграфе 7.5.

Определение

Для функций распределения Д С е 4х говорят, что Е доминирует 6 (Р>{ С) по отношению стохастического доминирования первого рода (или первого порядка), если

причем хотя бы для одного значения ? е 9? это неравенство является строгим.

Это означает, что график функции распределения Д?) располагается правее графика функции 6(0 (рис. 7.2).

Рис. 7.2. Стохастическое доминирование первого рода

Обратите внимание!

Если F(t) — функция распределения случайной величины ?, a G(t) — функция распределения случайной величины ц, то по определению F(t) = Р{?, = Р{?> е (-°°, 0} и G(t) = Р{ц = Р{г| g (-°°, 0}- Тогда соотношение F(t) < G(t), Vi е S.H означает, что вероятность того, что значения ^ принадлежат интервалу (-°°, i), не превосходит вероятность того, что значения г принадлежат тому же интервалу.

Пример стохастического доминирования. Об этом говорит сайт https://intellect.icu . Обозначим Р — функцию распределения случайной величины Пусть а > 0 — некоторая константа. Тогда р+д стохастически доминирует Р — Рс+Д >, Fi (рис. 7.3). Например, если ?, — это величина прибыли, полученная некоторым магазином в течение месяца, то, увеличив прибыль на заданное неслучайное число условных единиц, получим, что вероятность того, что величина прибыли ?, + а меньше любого заданного значения ? не превышает вероятность того, что величина % меньше этого значения ?. Иначе говоря, чем больше прибыль, тем с меньшей вероятностью она принимает малые значения.

Пример стохастического доминирования, если Р?(х) = 1 - ехр(-Х, х) — экспоненциальная функция распределения с параметром X > 0, то Рх >, РХ] при Х1 > Х2 (рис. 7.4).

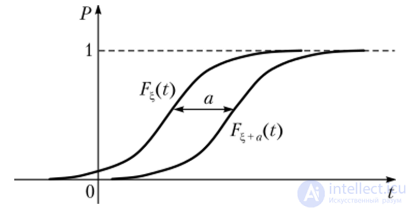
Рис. 7.3. Пример стохастического доминирования

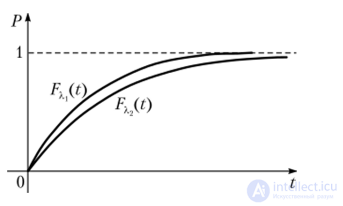
Рис. 7.4. Стохастическое доминирование, если функции распределения изменяются по экспоненте

Если функции распределения пересекаются (рис. 7.5), то нельзя утверждать, что одна из функций доминирует другую по отношению стохастического доминирования первого порядка.

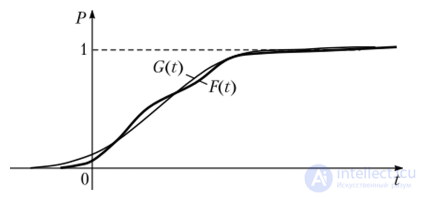
Рис. 75. Нарушение свойства стохастического доминирования первого рода

В этом случае можно рассмотреть так называемую накопленную функцию распределения, т.е. можно сравнивать площади под функциями распределения.

Определение

Для функций распределения Г. С, е Т говорят, что Р доминирует С (/-’ 2*,, С) по отношению стохастического доминирования второго рода (или второго порядка), если

Заметим, что стохастическое доминирование первого порядка влечет за собой стохастическое доминирование второго порядка, г.е. является более сильным свойством.

Обратите внимание!

Отношения стохастического доминирования нс обладают свойством полноты.

Исследование, описанное в статье про Построение бинарных отношений предпочтения на множестве вероятностных распределений, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Построение бинарных отношений предпочтения на множестве вероятностных распределений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений