Лекция
Привет, Вы узнаете о том , что такое Способы задания функций выбора, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Способы задания функций выбора , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Формализацией определения предпочтений ЛИР является задание функции выбора, определение и свойства которой были представлены в параграфе 7.1. Функция выбора С может быть задана или непосредственно ЛПР, или с помощью некоторого решающего правила.
Во многих задачах ЛПР может непосредственно описать свой выбор наилучших вариантов из некоторого имеющегося поднабора альтернатив.
Пример способа задания функции выбора. Выбирая в магазине какой- либо товар, например, сок, некоторый покупатель может выделить для себя двух наилучших производителей отечественных соков, наилучшего производителя импортных соков и из соков определенного вида, скажем яблочных, тог, который ему нравится больше всех.
В данном ситуации задача решена локально, и ЗПР в данном случае состоит в глобальном выборе наилучших из общего множества альтернатив.
Другим способом задания функции выбора является применение какого-либо решающего правила.
Определение
Решающим правилом называется критерий (или стратегия), позволяющий ЛПР разбить множество альтернатив X на два непересекающихся подмножества: «хороших» и «плохих» альтернатив.
В результате применения некоторого решающего правила множество альтернатив X разбивается на два непересекающихся подмножества X = X УХ,, где X = С(Х) — множество «хороших», а X, — множество «плохих» (нс подходящих) с точки зрения ЛПР альтернатив. Иначе говоря, решающее правило строит функцию выбора С следующим образом:
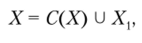
где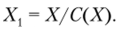 
Выбор соответствующего правила зависит от поставленной задачи, а также свойств множеств альтернатив и результатов.
Рассмотрим несколько подходов к построению функций выбора, отвечающих различным решающим правилам.
1. Об этом говорит сайт https://intellect.icu . Скалярная оптимизация. Выбор наиболее предпочтительных альтернатив осуществляется по скалярному критерию качества альтернативы, заданному е помощью целевой функции/:Х—> ЧЛ. Тогда подмножество «лучших» альтернатив 6'(Х) будет содержать те элементы х е X, на которых критерий качества достигает своего оптимума — максимума или минимума:
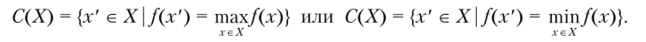
Другим случаем выбора наиболее предпочтительных вариантов является задание некоторого порогового значения с* для целевой функции:
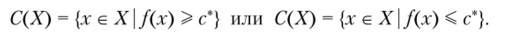
2. У словно-экстремальная оптимизация. В данном случае задается целевая функция /: X —*? Л и набор функций ...,/„: X —> Л. Выбор осуществляется методами математического программирования. Наиболее предпочтительными будут те элементы х’ е X, на которых целевая функция/(х) достигает своего оптимума — максимума или минимума:
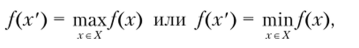
при условии выполнения дополнительных функциональных ограничений /?(х) < 0, г = 1, 2,..., п:
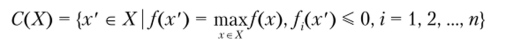
ил и
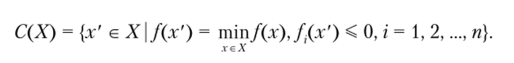
3. Доминирование, определенное заданным бинарным отношением Я. В данном случае выбираются альтернативы, которые предпочтительнее всех остальных альтернатив множества X по отношению строгого или нестрогого предпочтения К:
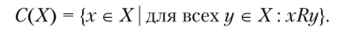
4. Принцип ограничений, определяемый бинарным отношением Я и заданным подмножеством альтернатив А с А. В данном случае выбираются альтернативы, которые предпочтительнее всех альтернатив из некоторого заданного подмножества альтернатив Л с Л по отношению строгого или нестрогого предпочтения:
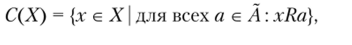
где Я — некоторое, заданное отношение предпочтения.
Обратите внимание!
В качестве целевой функции при использовании метода скалярной оптимизации построения решающего правила может выступать функция полезности и. Тогда решающее правило может быть построено следующим образом
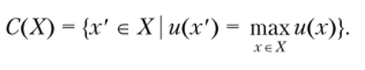
И поскольку функция полезности задает бинарное отношение на множестве альтернатив, то это же правило приводит к построению доминирования, определенного заданным бинарным отношением. Таким образом, в этом случае эти два принципа построения решающего правила являются эквивалентными.
Приведенный перечень решающих правил является далеко не полным. Выбор подходящего правила обусловливается конкретной задачей.
Исследование, описанное в статье про Способы задания функций выбора, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Способы задания функций выбора и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Комментарии