Лекция
Привет, сегодня поговорим про задачи принятия решений в условиях определенности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое задачи принятия решений в условиях определенности , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Общей частью методов принятия решений при многих критериях является отыскание множества Парето-оптимальных альтернатив из всего множества альтернатив. Рассмотрим ЗПР в условиях определенности – множество исходов совпадает с множеством альтернатив.
Пусть для оценивания исходов используется N критериев, причем большее значение критерия предпочтительнее меньшего. Тогда каждый исход (и альтернатива) будет характеризоваться вектором значений критериев (x1, x2, …, xN).
Вектор (x1, x2, …, xN) содержит полную информацию о ценности (полезности) этого исхода для ЛПР, и сравнение любых двух исходов заменяется сравнением их векторных оценок.
Векторная оценка x=(x1, x2, …, xN) доминирует по Парето векторную оценку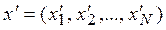 
(обозначение
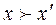), если для всех 
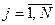выполняется неравенство 
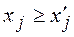и хотя бы для одного индекса j неравенство является строгим.
Векторная оценка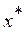 
называется Парето-оптимальной, если не существует такой векторной оценки x, что 
.
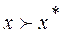Аналогично для исходов.
Альтернатива A1 доминирует над альтернативой A2, (обозначение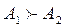
), если A1 не хуже, чем A2 по всем критериям, а как минимум по одному критерию лучше, или если векторная оценка исхода A1 доминирует по Парето векторную оценку исхода A2.
Альтернатива считается оптимальной по Парето, если нет альтернатив, доминирующих над ней.
Множество недоминируемых альтернатив образует множество Эджворта-Парето (Э-П).
Задача выделения множества Э-П обычно рассматривается как предварительная. За ней следует наиболее существенный этап принятия решений.
Различные методы принятия решений при многих критериях отличаются способом перехода к единой оценке полезности альтернатив. Можно выделить ряд групп таких методов.
В методах первой группы (прямые методы) зависимость общей полезности альтернативы от оценок по отдельным критериям известна заранее. Чаще всего используется вид зависимости, при котором определяются численные показатели важности критериев (веса), умножаемые на оценки по критериям (метод взвешенной суммы оценок критериев).
Во второй группе методов (методы компенсации) пытаются уравновесить (скомпенсировать) оценки одной альтернативами оценками другой, чтобы найти, какие оценки лучше. По идее, это наиболее простой метод, при котором человек выписывает достоинства и недостатки каждой из альтернатив и, вычеркивая попарно эквивалентные достоинства (недостатки), изучает то, что осталось.
В третьей группе (методы порогов несравнимости) задается правило сравнения двух альтернатив, при котором одна альтернатива считается лучше другой (например, оценки первой по большинству критериев лучше). В соответствии с заданным правилом альтернативы делятся (попарно) на сравнимые (одна лучше другой, либо эквивалентные) и несравнимые. Измеряя отношение сравнимости, получаем разное число пар сравнимых альтернатив.
В четвертой группе (аксиоматические методы) определяется ряд свойств, которым должна удовлетворять зависимость общей полезности альтернативы от оценок по отдельным критериям. Эти свойства (называемые аксиомами) проверяются путем получения информации от лиц, принимающих решение. В соответствии с этой информацией делается вывод о той или иной форме зависимости.
Для прямых методов характерна зависимость полезности альтернативы от ее оценок по критериям, которая задается без всяких теоретических оснований, а параметры этой зависимости либо также задаются, либо непосредственно оцениваются ЛПР.
3.2.1. Метод взвешенной суммы. Зависимость имеет следующий вид:
,
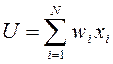где wi – вес (важность) i-го критерия, назначаемый ЛПР; xi – оценка альтернативы по i-му критерию.
Логическим обоснованием метода взвешенной суммы является представление об общей полезности альтернативы как о сумме оценок нескольких независимых критериев. Коэффициенты wi выражают относительную важность оценок критериев.
3.2.2. Мультипликативный метод. Зависимость имеет следующий вид:
.
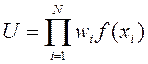Чаще всего принимают f(xi)=xi. В некоторых случаях используют метод с зависимостью f(xi)=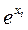 
. Об этом говорит сайт https://intellect.icu . Путем логарифмирования мультипликативный метод можно свести к суммированию логарифмов оценок, поэтому иногда его объединяют с методом взвешенных сумм. Логическим обоснованием мультипликативного метода является представление об оценках по критериям как о вероятностях достижения определенных показателей качества.
3.2.3. Лексикографическое упорядочивание. В данном методе критерии упорядочиваются по важности, после чего лучшей считается альтернатива, имеющая более высокую оценку по более важному критерию К1 вне зависимости от оценок по прочим критериям. Если оценки по критерию К1 совпадают, альтернативы сравниваются по критерию К2 и т.д.
3.2.4. Метод БОФа. Данный метод предложен в Быстровым Олегом Филаретовичем для сравнительной оценки инвестиционных проектов по множеству показателей [7, с. 54-63].
Целью метода является определение наиболее приемлемого проекта по заданным показателям.
Данный метод может использоваться для оценки любого множества объектов по множеству показателей (критериев) – принятие решений при многих критериях в условиях определенности.
Постановка задачи
Дано:
K – количество объектов, M – количество показателей для сравнения объектов;
R=(R1, R2, … RM) – ранжирование показателей по важности;
|Cij| – матрица значений показателей для объектов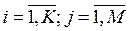 
.
Требуется упорядочить объекты или выбрать лучший объект.
Описание алгоритма
Метод БОФа состоит из следующих этапов.
1. Отобрать оптимальное количество показателей. Обозначим показатели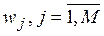
.
2. Проранжировать показатели по важности в соответствии с предпочтениями ЛПР. Обозначим ранги показателей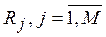 
.
3. Определить весовые коэффициенты каждого показателя.
Весовые коэффициенты показателей wj определяются по формуле 3.2.1 и затем нормируются по формуле 3.2.2:
 |
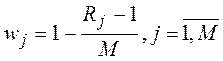(3.2.1) |
 |
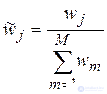(3.2.2) |
4. Проранжировать объекты по важности в соответствии с предпочтениями ЛПР по каждому показателю. Обозначим значения показателей для объектов Pji, ранги объектов по показателям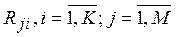 
, где K – количество объектов.
5. Определить весовые коэффициенты каждого объекта по каждому показателю.
Весовые коэффициенты объектов по каждому показателю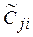 
определяются по формуле 3.2.3 и затем нормируются по формуле 3.2.4:
 |
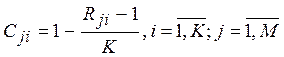(3.2.3) |
 |
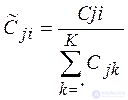(3.2.4) |
Таким образом, для расчета весовых коэффициентов используются отношения порядка между объектами. Однако использованиепорядковой информации может привести к утрате части полезной информации. При необходимости учета количественной информации весовые коэффициенты показателей рассчитываются по формуле 3.2.5, если большие значения показателей предпочтительнее меньших, или по формуле 3.2.6, если меньшие значения предпочтительнее больших. При этом этап 4 (ранжирование объектов по каждому показателю) опускается.
 |
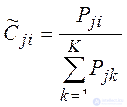(3.2.5) |
Pji – значение показателя j для объекта i.
 |
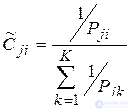(3.2.6) |
6. Рассчитать значения обобщенного показателя для каждого объекта .
 |
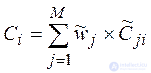(3.2.7) |
7. Проранжировать объекты в соответствии со значениями обобщенных показателей и/или определить лучший объект.
Требуется выбрать лучший инвестиционный проект для реализации. Для сравнения проектов были выбраны показатели:
NVP (чистый приведенный доход);
IRR (внутренняя норма рентабельности);
PI (индекс прибыльности);
PP (срок окупаемости);
ARR (ср. норма прибыли на инвестиции).
Информация о проектах представлена в табл. 3.1, ранжирование показателей по важности – в табл. 3.2.
Таблица 3.1
Информация о проектах
|
Показатели |
Проекты |
|||
|
Проект 1 |
Проект 2 |
Проект 3 |
Проект 4 |
|
|
NVP (чистый приведенный доход) |
557, 9 |
603,3 |
561,0 |
356,8 |
|
IRR (внутренняя норма рентабельности) |
22,7% |
25% |
27,1% |
25,3% |
|
PI (индекс прибыльности) |
1,46 |
1,5 |
1,47 |
1,3 |
|
PP (срок окупаемости) |
4 года |
4 года |
3 года |
2 года |
|
ARR (ср. норма прибыли на инвестиции) |
55% |
55,3% |
45% |
28,3% |
Таблица 3.2
Ранги показателей
|
Ранг (Rj) |
NPV |
IRR |
PI |
PP |
ARR |
|
W1 |
W2 |
W3 |
W4 |
W5 |
|
|
1 |
2 |
3 |
4 |
5 |
Таким образом, этап 1 и этап 2 уже выполнены.
Этап 3. Определение весовых коэффициентов показателей и нормирование их значений.
, 
, 
, 
, 
.
, 
, 
,
,
.
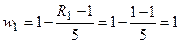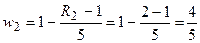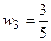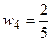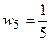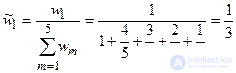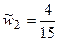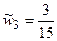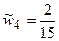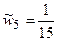Этап 4. Ранжирование объектов по каждому показателю.
Проекты сравниваются по каждому показателю и результаты заносятся в таблицу 3.3, Rji – ранг объекта с номером i по показателю с номером j.
Таблица 3.3
Ранги проектов по показателям
|
|
Проект 1 |
Проект 2 |
Проект 3 |
Проект 4 |
|
W1 |
R11=3 |
1 |
2 |
4 |
|
W2 |
4 |
3 |
1 |
2 |
|
W3 |
3 |
1 |
2 |
4 |
|
W4 |
3,5 |
3,5 |
2 |
1 |
|
W5 |
2 |
1 |
3 |
4 |
Этап 5. Определение весовых коэффициентов объектов по каждому показателю и нормирование полученных значений.
Вычислим значения показателя 1 по всем объектам.
,
,
,
.
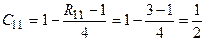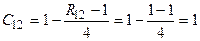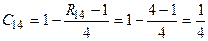Пронормируем полученные значения.
,
,
, 
.
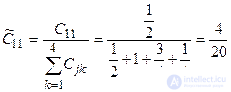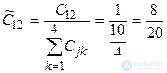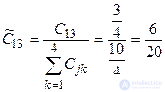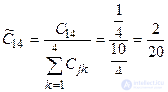Значения остальных весовых коэффициентов объектов по показателям вычисляются аналогично.
Этап 6. Расчет значений обобщенного показателя для объектов.
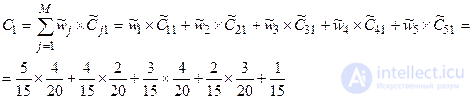
Аналогично вычисляем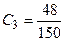 
,
,
.
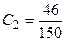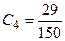Этап 7. Таким образом, лучшим является проект 3, на втором месте проект 2, затем идут проекты 4 и 1.
Надеюсь, эта статья об увлекательном мире задачи принятия решений в условиях определенности, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое задачи принятия решений в условиях определенности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений