Описание математической модели предпочтений в условиях вероятностной неопределенности кратко

Привет, Вы узнаете о том , что такое Описание математической модели предпочтений в условиях вероятностной неопределенности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Описание математической модели предпочтений в условиях вероятностной неопределенности , настоятельно рекомендую прочитать все из категории Теория принятия решений.

До сих пор мы считали, что состояние среды является неизменным. Если же это не гак, то задача построения предпочтений становится более сложной. Рассмотрим такие случаи более подробно.

Обозначим через — множество всех возможных результатов, полученных при принятии решения, X — множество всевозможных альтернатив задачи, 5 — множество всевозможных состояний среды. Будем предполагать, что каждый получаемый в ЗПР результат г е /?, зависит как от выбираемой ЛПР альтернативы х е X из множества всевозможных альтернатив X, так и от состояния среды 5 е .9, которое является случайным элементом.

Тогда функцией выбора будет называться отображение

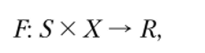
ставящее в соответствие определенный результат каждой альтернативе и случайному состоянию среды.

Обратите внимание!

Поскольку каждый результат г е Л зависит также и от случайного состояния среды, этот результат сам является некоторым случайным элементом.

В данном случае по полученному результату нельзя однозначно сказать, выбор какой из альтернатив является наилучшим, поскольку на результат влияет также и случайная компонента, которую нельзя полностью контролировать.

Для того чтобы строго описать возникшие случайности, необходимо задать вероятностные структуры на множествах 5 и /?!.

Зададим вероятностную структуру на множестве возможных состояний среды *9 следующим образом. Об этом говорит сайт https://intellect.icu . Событием или случайным событием А множества .9 называется любое его подмножество А а Я. Зададим множество 3 -

1 Познакомиться с основными понятиями теории вероятностей можно, например, в книгах: Боровков А. А. Теория вероятностей. М.: УРСС, 1999. 470 с.; Кремер Н. Ш. Теория вероятностей и математическая статистика : учебник для вузов. М.: Юнити-Дана, 2001. 543 с.

а-алгебру событий, т.е. множество случайных событий с системой, замкнутой относительно взятия дополнения, счетных объединений и пересечений. В этом случае говорят, что множество 5 наделено структурой измеримого пространства: (S, 3). На событиях из ст-алгебры 3 зададим вероятность (вероятностную меру) Ру т.е. сопоставим каждому событию Ау принадлежащему а-алгебре 3, некоторое число Р{/1), являющееся вероятностью этого события. Тогда получим классическую «вероятностную тройку»

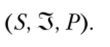
Наделим также множество результатов структурой измеримого пространства (R, В)у т.е. зададим на нем а-алгебру случайных событий В. Тогда для каждой альтернативы х е X измеримое относительно а-алгебр (3, В) отображение Fx = F(x): S R, где F — заданная выше функция выбора, образует случайный элемент множества результатов R. При этом вероятностное распределение Рх на (R, В) для случайного события В е В будет задаваться следующим образом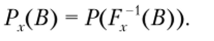

Обратите внимание!

Для всякого случайного события В е В множество Тд В) является случайным событием пространства (5, 3), т.е. Тх. В) е 3.

Данный результат подтверждает возможность определения вероятности

Р(р;в)).

Таким образом, каждое решение или каждая выбранная ЛПР альтернатива приводит к некоторому вероятностному распределению, и задача выбора наилучшего решения сводится к задаче выбора наилучшего распределения в классе {РхУ х е X). Так как описанное распределение порождает некоторую случайную величину ?д., возникает задача сравнения вероятностных распределений (или случайных величин), отвечающих различным альтернативам.

Распределение случайной величины полностью определяется ее функцией распределения 7(?) = Р{^х < ?}, заданной на множестве вещественных чисел (? € 9?). Обозначим через Т совокупность всевозможных вещественных функций распределения, порождаемых заданной ЗПР:

Таким образом, система предпочтений ЛПР в случае ЗПР в условиях вероятностной неопределенности будет строиться на множестве Т.

Исследование, описанное в статье про Описание математической модели предпочтений в условиях вероятностной неопределенности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Описание математической модели предпочтений в условиях вероятностной неопределенности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений