Лекция
Привет, сегодня поговорим про введение в теорию принятия решений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое введение в теорию принятия решений , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Теория принятия решений (ТПР) – это совокупность математических дисциплин, в которых исследуются лишь вполне четко описанные и формализованные модели выбора решений при тех или иных начальных условиях, ограничениях на выбор и возможности выбора.
Таким образом, предметом ТПР является изучение процессов, направленных на принятие решений, и способов их формализации.
Под принятием решений будем понимать человеческую деятельность, направленную на выбор наилучшего варианта действий в определенной ситуации .
Пусть имеется некоторая система. В ней выделена управляемая подсистема (объект управления) и управляющая подсистема. Сама система находится в некоторой среде (Рис. 1.1).
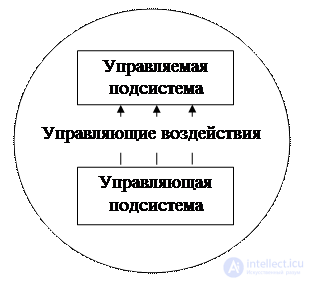
Рис. 1.1. Принятие решений как процесс управления
Управляющая подсистема может воздействовать на объект управления с помощью того или иного управляющего действия, в результате чего объект управления переходит в новое состояние.
Возможные варианты управляющих действий называются альтернативами или решениями.
Целью управляющего действия является перевод объекта управления в наиболее предпочтительное для управляющей подсистемы состояние. Новое состояние объекта определяется двумя факторами: выбранным управляющим действием и состоянием среды.
Важно то, что управляющая подсистема не может воздействовать на среду и, возможно, даже не имеет информации о состоянии среды.
Выбор управляющей подсистемой конкретного управляющего действия (по-другому, альтернативы или решения) называется принятием решения.
Целью принятия решения является нахождение оптимального решения, то есть решения, которое по тем или иным признакам предпочтительные перед другими.
Участника процесса принятия решения называют лицом, принимающим решение (ЛПР).
В процессе принятия решений может принимать участие одно или несколько ЛПР.
Итак, для описания ситуации, в которой происходит принятие решения, необходимо задать три множества:
A – множество альтернатив или управляющих действий,
B – множество состояний среды,
C – множество возможных исходов.
Под термином «исходы» понимаются состояния, в которые может перейти управляемая подсистема.
Так как состояние управляемой подсистемы определяется выбором управляющего действия и состоянием среды, то каждой паре (a, b), где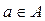 
, 
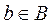, соответствует определенный исход 
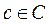. Это означает, что существует функция 
. Назовем ее реализационной функциейи обозначим F.
Кроме того, для принятия решения каждый исход необходимо оценить с точки зрения лица, принимающего решение, то есть сформулировать еще и оценочную систему. Для оценки исходов может использоваться:
Важно то, что оценивание исходов носит субъективный характер, так как оно производится с точки зрения ЛПР.
Таким образом, построение математической модели задачи принятия решений сводится к заданию множеств A, B, C, реализационной функции F и оценочной системы (в виде функции полезности, отношений предпочтения и т.д.) [2, с. 11 – 14].
Традиционно принято выделять следующие типы задач принятия решений:
Например, члены семьи упорядочивают по степени необходимости будущие покупки.
При покупке автомобиля человек разбивает все варианты на два класса – автомобили, подходящие по цене, и автомобили, стоимость которых превышает пороговую величину. Об этом говорит сайт https://intellect.icu . Это пример задачи классификации.
Задачи третьего типа очень часто встречаются на практике. После того, как известны все автомобили, подходящие по цене, человек выбирает лучший автомобиль – тот, который в конечном итоге он купит.
Кроме того, принятие решений может происходить в ситуациях двух типов. В первом случае осуществляется анализ заданных альтернатив, множество альтернатив замкнуто. Во втором случае строится решающее правило, позволяющее оценивать любые альтернативы.
Например, требуется определить лучший бассейн города. В процессе участвует группа специалистов, каждый из которых строит ранжирование бассейнов. Затем на основе индивидуальных ранжирований строится агрегированное ранжирование и таким образом выявляется лучший бассейн. В данном случае осуществляется анализ заданных альтернатив – бассейнов города.
Примером ситуации второго типа является принятие решений о выдаче кредита в банке. Решающее правило должно быть выработано до того, как в банк начнут обращаться клиенты. При обращении клиента в банк каждый раз должна производиться оценка согласно решающему правилу.
Остановимся на наиболее важных этапах принятия решений, а именно:
В научной литературе предложено несколько классификаций задач принятия решений (ЗПР), основанных на различных системах признаков .
Наиболее общими и существенными признаками классификации, встречающимися в большинстве работ, являются:
1.4.1 Тип связи между множеством альтернатив и множеством исходов. В любой ЗПР фигурирует два множества элементов – множество альтернатив и множество исходов. По данному признаку ЗПР делятся на три группы.
ЗПР в условиях определенности – существует одиночная связь между множеством альтернатив и исходов.
Пример. Задача построения рейтинга компьютерных магазинов города.
ЗПР в условиях вероятной определенности или в условиях риска – каждой альтернативе ставится в соответствие набор исходов с некоторыми вероятностями их осуществления, эти вероятности известны ЛПР.
Пример. Пусть мастерская имеет n станков, причем ремонт отказавшего станка производится индивидуально, а если станки не отказывают, то через T интервалов времени производится профилактический ремонт всех станков. Задача заключается в определении оптимального значения количества интервалов T, при котором общие затраты на ремонт будут минимальны. Очевидно, что задача может быть решена, если известна вероятность pt отказа одного станка в момент времени t. Эта неопределенность и представляет в данном случае элемент «риска».
ЗПР в условиях неопределенности – информация о связях между множеством альтернатив и множеством исходов отсутствует или неполная.
Пример. Игра в покер, шахматы.
1.4.2. Количество критериев. По количеству критериев различают однокритериальные (скалярные) ЗПР и многокритериальные (векторные) ЗПР.
ЛПР при принятии решений руководствуется целями, которые нужно достигнуть. Цели ставится в соответствие критерий или совокупность критериев, с помощью которых можно оценить степень достижения этой цели.
Примеры. В качестве примера однокритериальной ЗПР рассмотрим задачу об оптимальном размере закупаемой партии товара [2, с. 20 – 21].
Фирма закупает некоторый товар в течение планового периода партиями одинаковой величины. Закупленный товар используется с постоянной скоростью. Как только запас товара кончается, закупается следующая партия и т. д. Неизрасходованный товар фирма хранит на складе за определенную плату.
Известны следующие величины:
Требуется определить такой размер закупаемой партии товара, при котором затраты фирмы будут минимальными.
В качестве примера многокритериальной ЗПР можно привести задачу выбора кандидата на должность. Критериями оценки кандидатов являются образование, опыт работы, возраст и т.д.
1.4.3. Количество лиц, участвующих в принятии решения. Также выделяют индивидуальные и групповые решения в зависимости от числа экспертов или лиц, принимающих решение.
Если в процессе принятия решений участвуют два лица и их интересы противоположны, то принятием решения в такой ситуации занимается теория антагонистических игр.
Примером метода группового принятия решений является рейтинговое голосование в Думе. Допустим, на роль спикера претендуют 5 человек. Тогда каждый из депутатов дает свое ранжирование (возможно нестрогое) этих пяти кандидатов. При этом возникает задача построения обобщенного или компромиссного ранжирования, на основе которого и будет определено, кто же станет спикером.
При групповой экспертизе часто возникают ситуации следующих типов: у экспертов разные мнения по поводу набора критериев, у экспертов разные мнения о сравнительной значимости критериев, эксперты дают разные оценки альтернатив по критериям. Можно сказать, что методы группового выбора позволяют структурировать множество альтернатив в ситуации «разноголосицы» суждений экспертов .
1.4.4. По типу модели (решающего правила).
Решающее правило называется субъективным, если, основываясь на одной и той же исходной информации, различные исследователи приходят к различным выводам.
Возможны следующие варианты:
Построение моделей рассматривается в рамках исследования операций как средство отражения объективно существующей реальности. Когда модель, правильно отражающая действительность, найдена, критерий оптимальности установлен, оптимальное решение может быть получено единственно возможным образом. Опираясь на одни и те же данные, различные специалисты-аналитики должны получать одинаковые результаты .
1.4.5. Зависимость критерия оптимальности и ограничивающих факторов от времени. По этому признаку ЗПР делятся на два больших класса: статические и динамические.
Задача называется статической, если принятие решения происходит в наперед известном и не изменяющемся информационном состоянии, или в статических ЗПР показатель эффективности и ограничивающие условия не зависят от времени.
Если информационное состояние в ходе принятия решения сменяют друг друга, то задача называется динамической.
1.4.6. Использование эксперимента для получения информации. По признаку использования эксперимента для получения информации ЗПР классифицируют на две группы: ЗПР по априорным данным и ЗПР по апостериорным данным.
Принятие решений по априорным данным характерно для условий определенности и частично для условий вероятной определенности. В условиях неопределенности априорной информации очень мало, поэтому необходимо получение новой информации путем проведения экспериментов. Результаты экспериментов дают апостериорную информацию.
Рис. 1.5 −Взаимосвязь задач выбора
На рис. 1.2 представлена связь между классами задач принятия решений и направлениями ТПР.
Далее будут подробно рассмотрены многокритериальные ЗПР в условиях определенности и риска. В условиях неопределенности мы остановимся на однокритериальных ЗПР и многокритериальных ЗПР, рассмотрим также групповые или коллективные ЗПР.
Рис. 1.2. Классификация ЗПР
Надеюсь, эта статья об увлекательном мире введение в теорию принятия решений, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое введение в теорию принятия решений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений